Архитектура нейросетей
Архитектура нейросетей
Содержание: - Обзор архитектуры - Слои ConvNet - Сверточный слой - Слой пула - Слой нормализации - Полностью подключенный слой - Преобразование полносвязных слоев в сверточные слои - Архитектуры ConvNet - Узоры слоев - Шаблоны для определения размеров слоев - Тематические исследования (LeNet / AlexNet / ZFNet / GoogLeNet / VGGNet) - Вычислительные соображения - Дополнительные материалы
Сверточные нейронные сети (CNNs / ConvNets)
Сверточные нейронные сети очень похожи на обычные нейронные сети из предыдущей главы: они состоят из нейронов, которые имеют обучаемые веса и смещения. Каждый нейрон получает некоторые входные данные, выполняет скалярное произведение и опционально следует за ним с нелинейностью. Вся сеть по-прежнему выражает одну дифференцируемую функцию оценки: от пикселей необработанного изображения на одном конце до оценок классов на другом. И у них по-прежнему есть функция потерь (например, SVM/Softmax) на последнем (полностью подключенном) слое, и все советы/рекомендации, которые мы разработали для обучения обычным нейронным сетям, по-прежнему применимы.
Так что же меняется? Архитектуры ConvNet явно предполагают, что входные данные являются изображениями, что позволяет нам закодировать определенные свойства в архитектуре. Это делает функцию forward более эффективной для реализации и значительно сокращает количество параметров в сети.
Обзор архитектуры
Напомним: обычные нейронные сети. Как мы видели в предыдущей главе, нейронные сети получают входные данные (один вектор) и преобразуют их через серию скрытых слоев. Каждый скрытый слой состоит из набора нейронов, где каждый нейрон полностью связан со всеми нейронами предыдущего слоя, и где нейроны в одном слое функционируют совершенно независимо и не имеют общих связей. Последний полносвязный слой называется «выходным слоем» и в настройках классификации представляет собой баллы класса.
Обычные нейронные сети плохо масштабируются до полных изображений. В CIFAR-10 изображения имеют размер всего 32x32x3 (32 в ширину, 32 в высоту, 3 цветных канала), поэтому один полностью связанный нейрон в первом скрытом слое обычной нейронной сети будет иметь 32 * 32 * 3 = 3072 веса. Это количество все еще кажется управляемым, но очевидно, что эта полностью связанная структура не масштабируется до более крупных изображений. Например, изображение более приличного размера, например, 200x200x3, приведет к нейронам с весом 2002003 = 120 000. Более того, мы почти наверняка хотели бы иметь несколько таких нейронов, чтобы параметры быстро складывались! Очевидно, что такая полная связность является расточительной, а огромное количество параметров быстро приведет к переобучению.
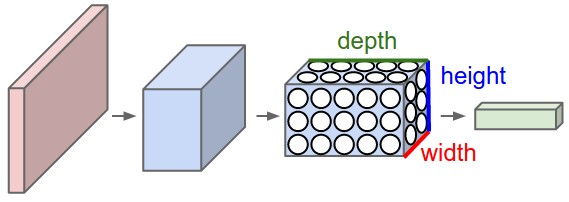
3D объемы нейронов. Сверточные нейронные сети используют тот факт, что входные данные состоят из изображений, и они ограничивают архитектуру более разумным образом. В частности, в отличие от обычной нейронной сети, слои ConvNet имеют нейроны, расположенные в трех измерениях: ширина, высота, глубина. (Обратите внимание, что слово «глубина» здесь относится к третьему измерению объема активации, а не к глубине полной нейронной сети, которая может относиться к общему количеству слоев в сети.) Например, входные изображения в CIFAR-10 представляют собой входной объем активаций, а объем имеет размеры 32х32х3 (ширина, высота, глубина соответственно). Как мы вскоре увидим, нейроны в слое будут соединены только с небольшой областью слоя перед ним, а не со всеми нейронами в полном объеме. Более того, итоговый выходной слой для CIFAR-10 будет иметь размеры 1x1x10, так как к концу архитектуры ConvNet мы сведем полное изображение к единому вектору оценок классов, расположенных по размерности глубины. Вот визуализация:
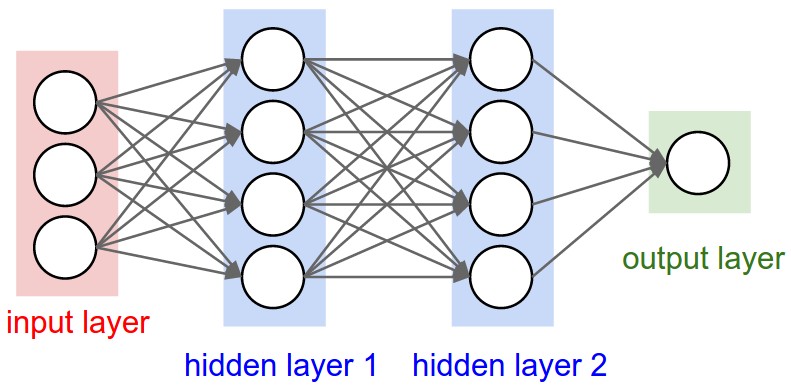
Сверху: обычная 3-слойная нейронная сеть.
Снизу: ConvNet располагает свои нейроны в трех измерениях (ширина, высота, глубина), как это визуализировано в одном из слоев. Каждый слой ConvNet преобразует входной объем 3D в объем активации нейронов на выходе 3D. В этом примере красный входной слой содержит изображение, поэтому его ширина и высота будут соответствовать размерам изображения, а глубина будет равна 3 (красный, зеленый, синий каналы).
ConvNet состоит из слоев. У каждого слоя есть простой API: он преобразует входной 3D-объем в выходной 3D-объем с помощью некоторой дифференцируемой функции, которая может иметь или не иметь параметры.
Слои, используемые для построения ConvNet
Как мы уже описывали выше, простая ConvNet представляет собой последовательность слоев, и каждый слой ConvNet преобразует один объем активаций в другой с помощью дифференцируемой функции. Мы используем три основных типа слоев для построения архитектур ConvNet: сверточный слой, слой пула и полносвязный слой (точно так же, как это видно в обычных нейронных сетях). Мы сложим эти слои, чтобы сформировать полноценную архитектуру ConvNet.
Пример архитектуры: обзор. Мы рассмотрим это более подробно ниже, но простой ConvNet для классификации CIFAR-10 может иметь архитектуру [INPUT - CONV - RELU - POOL - FC]. Более подробно:
- INPUT [32x32x3] будет содержать исходные значения пикселей изображения, в данном случае изображение шириной 32, высотой 32 и с тремя цветовыми каналами R,G,B.
- Слой CONV будет вычислять выходные данные нейронов, которые соединены с локальными областями на входных данных, каждый из которых вычисляет скалярное произведение между их весами и небольшой областью, к которой они подключены во входном объеме. Это может привести к объему [32x32x12], если мы решили использовать 12 фильтров.
- Слой RELU будет применять функцию поэлементной активации, такую как max(0,х) с пороговым значением на нуле. При этом размер тома остается неизменным ([32x32x12]).
- Слой POOL выполнит операцию понижения дискретизации вдоль пространственных измерений (ширина, высота), в результате чего будет получен объем, такой как [16x16x12].
- Уровень FC (т.е. полностью подключенный) будет вычислять баллы класса, в результате чего будет получен объем размера [1x1x10], где каждое из 10 чисел соответствует баллу класса, например, среди 10 категорий CIFAR-10. Как и в случае с обычными нейронными сетями и как следует из названия, каждый нейрон в этом слое будет связан со всеми числами в предыдущем объеме.
Таким образом, ConvNet слой за слоем преобразуют исходное изображение от исходных значений пикселей до итоговых оценок класса. Обратите внимание, что некоторые слои содержат параметры, а другие нет. В частности, слои CONV/FC выполняют преобразования, которые являются функцией не только активации входного объема, но и параметров (весов и смещений нейронов). С другой стороны, слои RELU/POOL будут реализовывать фиксированную функцию. Параметры в слоях CONV/FC будут обучаться с помощью градиентного спуска, чтобы оценки классов, вычисляемые ConvNet, соответствовали меткам в обучающем наборе для каждого изображения.
Вкратце:
- Архитектура ConvNet в простейшем случае представляет собой список слоев, которые преобразуют объем изображения в выходной объем (например, содержат оценки классов)
- Существует несколько различных типов слоев (например, CONV/FC/RELU/POOL на сегодняшний день являются наиболее популярными)
- Каждый слой принимает входной 3D-объем и преобразует его в выходной 3D-объем с помощью дифференцируемой функции
- Каждый слой может иметь или не иметь параметры (например, у CONV/FC есть, у RELU/POOL нет)
- Каждый слой может иметь или не иметь дополнительные гиперпараметры (например, у CONV/FC/POOL есть, у RELU нет)
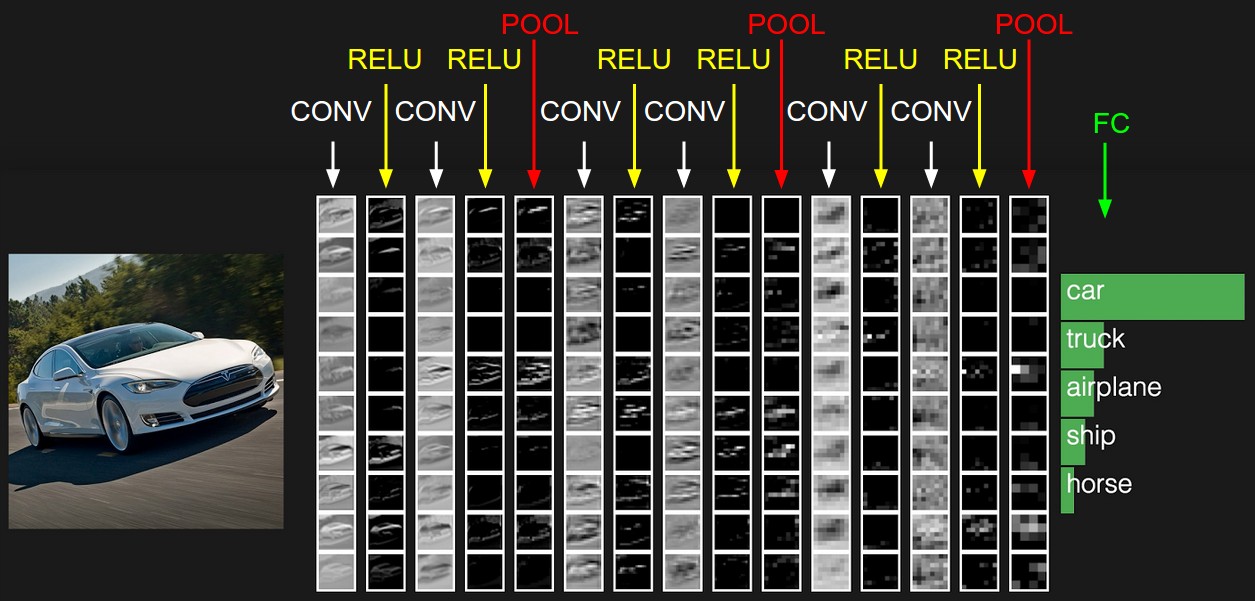
Активация примера архитектуры ConvNet. Начальный том хранит необработанные пиксели изображения (слева), а последний том хранит оценки класса (справа). Каждый объем активаций на пути обработки отображается в виде столбца. Так как визуализировать 3D-объемы сложно, мы выкладываем срезы каждого тома в ряды. Последний объем слоя содержит баллы для каждого класса, но здесь мы визуализируем только отсортированные 5 лучших баллов и печатаем этикетки каждого из них. Полный прототип веб-версии приведен в шапке нашего веб-сайта. Архитектура, показанная здесь, представляет собой крошечную сеть VGG, о которой мы поговорим позже.
Теперь мы опишем отдельные слои и детали их гиперпараметров и связуемости.
Сверточный слой
Уровень Conv является основным строительным блоком сверточной сети, который выполняет большую часть тяжелой вычислительной работы.
Обзор и интуиция без мозгов. Давайте сначала обсудим, что вычисляет слой CONV без аналогий между мозгом и нейронами. Параметры слоя CONV состоят из набора обучаемых фильтров. Каждый фильтр имеет небольшие пространственные размеры (по ширине и высоте), но простирается на всю глубину входного объема. Например, типичный фильтр на первом слое ConvNet может иметь размер 5x5x3 (т. е. 5 пикселей в ширину и высоту, и 3, поскольку изображения имеют глубину 3, цветовые каналы). Во время прямого прохода мы скользим (точнее, свертываем) каждый фильтр по ширине и высоте входного объема и вычисляем точечные произведения между входами фильтра и входом в любом положении. Когда мы перемещаем фильтр по ширине и высоте входного объема, мы создадим двумерную карту активации, которая дает ответы этого фильтра в каждом пространственном положении. Интуитивно сеть будет изучать фильтры, которые активируются, когда они видят какой-либо визуальный признак, такой как край определенной ориентации или пятно определенного цвета на первом слое, или, в конечном итоге, целые соты или узоры, похожие на колеса, на более высоких слоях сети. Теперь у нас будет целый набор фильтров в каждом слое CONV (например, 12 фильтров), и каждый из них создаст отдельную двухмерную карту активации. Мы наложим эти карты активации вдоль измерения глубины и получим выходной объем.
Взгляд на мозг. Если вы являетесь поклонником аналогий между мозгом и нейронами, то каждая запись в 3D-объеме вывода также может быть интерпретирована как выход нейрона, который смотрит только на небольшую область на входе и разделяет параметры со всеми нейронами слева и справа в пространстве (поскольку все эти числа являются результатом применения одного и того же фильтра).
Теперь мы обсудим детали соединений нейронов, их расположение в пространстве и схему совместного использования параметров.
Местная связность. Когда речь идет о многомерных входных данных, таких как изображения, как мы видели выше, нецелесообразно соединять нейроны со всеми нейронами в предыдущем томе. Вместо этого мы будем подключать каждый нейрон только к локальной области входного объема. Пространственная протяженность этой связности является гиперпараметром, называемым рецептивным полем нейрона (эквивалентно размеру фильтра). Степень связности вдоль оси глубины всегда равна глубине входного объема. Важно еще раз подчеркнуть эту асимметрию в том, как мы трактуем пространственные размеры (ширину и высоту) и размеры глубины: соединения локальны в 2D-пространстве (по ширине и высоте), но всегда полны по всей глубине входного объема.
Пример 1. Например, предположим, что входной объем имеет размер [32x32x3] (например, изображение RGB CIFAR-10). Если рецептивное поле (или размер фильтра) равно 5x5, то каждый нейрон в слое Conv будет иметь веса в области [5x5x3] во входном объеме, что в сумме составляет 5x5x3 = 75 весов (и параметр смещения +1). Обратите внимание, что степень связности вдоль оси глубины должна быть равна 3, так как это глубина входного объема.
Пример 2. Предположим, что входной объем имеет размер [16x16x20]. Затем, используя пример с размером рецептивного поля 3x3, каждый нейрон в слое Conv теперь будет иметь в общей сложности 3x3x20 = 180 соединений с входным объемом. Обратите внимание, что, опять же, связность является локальной в 2D-пространстве (например, 3x3), но полной по глубине ввода (20).
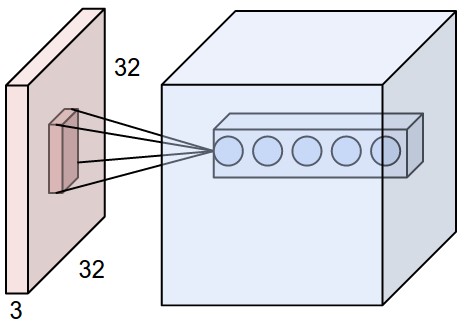
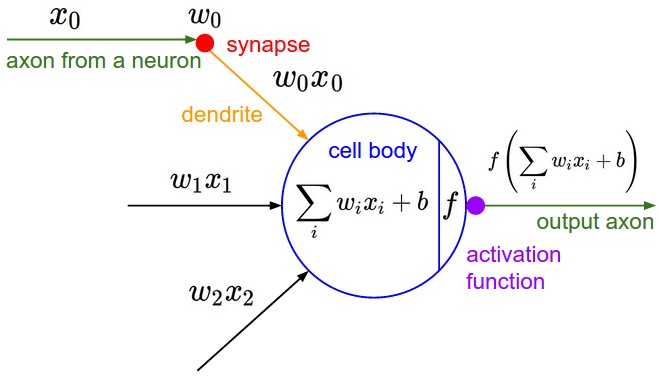
Сверху: Пример входного объема красным цветом (например, изображение CIFAR-10 размером 32x32x3) и пример объема нейронов в первом сверточном слое. Каждый нейрон в сверточном слое пространственно связан только с локальной областью во входном объеме, но на всю глубину (т.е. со всеми цветовыми каналами). Обратите внимание, что в глубине есть несколько нейронов (5 в этом примере), все они смотрят на одну и ту же область на входе: линии, которые соединяют этот столбец из 5 нейронов, не представляют веса (т.е. эти 5 нейронов не имеют одинаковых весов, но они связаны с 5 разными фильтрами), они просто указывают на то, что эти нейроны связаны или смотрят на одно и то же рецептивное поле или область входного объема. т.е. они имеют одно и то же рецептивное поле, но не одинаковые веса. Снизу: Нейроны из главы «Нейронные сети» остаются неизменными: они по-прежнему вычисляют скалярное произведение своих весов с последующим нелинейным значением, но их связность теперь ограничена локальными пространственными данными.
Пространственное расположение. Мы объяснили связь каждого нейрона в слое Conv с входным объемом, но мы еще не обсуждали, сколько нейронов находится в выходном объеме или как они организованы. Три гиперпараметра контролируют размер выходного объема: глубина, шаг и нулевое отступление. Мы обсудим их далее:
- Во-первых, глубина выходного объема — это гиперпараметр: он соответствует количеству фильтров, которые мы хотели бы использовать, каждый из которых учится искать что-то свое во входных данных. Например, если первый сверточный слой принимает в качестве входных данных исходное изображение, то различные нейроны в измерении глубины могут активироваться в присутствии различных ориентированных краев или цветовых пятен. Мы будем называть набор нейронов, которые смотрят на одну и ту же область входных данных, столбцом глубины (некоторые люди также предпочитают термин «волокно»).
- Во-вторых, мы должны указать шаг, с которым мы перемещаем фильтр. Когда шаг равен 1, мы перемещаем фильтры по одному пикселю за раз. Когда шаг равен 2 (или редко 3 или более, хотя на практике это редкость), фильтры прыгают на 2 пикселя за раз, когда мы их перемещаем. Это позволит производить меньшие объемы выпуска в пространственном отношении.
- Как мы скоро увидим, иногда будет удобно заполнять входной объем нулями по границе. Размер этого нулевого отступа является гиперпараметром. Приятная особенность нулевого заполнения заключается в том, что он позволяет нам контролировать пространственный размер выходных объемов (чаще всего, как мы скоро увидим, мы будем использовать его для точного сохранения пространственного размера входного объема, чтобы ширина и высота входного и выходного объема были одинаковыми).
Мы можем вычислить пространственный размер выходного объема как функцию от размера входного объема (W), размер рецептивного поля нейронов Conv слоя (F), шаг, с которым они наносятся (S) и количество использованного нулевого заполнения (P) на границе. Вы можете убедиться в том, что правильная формула для расчета количества нейронов «поместится» по формуле (W−F+2P)/S+1. Например, для входа 7x7 и фильтра 3x3 со stride 1 и pad 0 мы получим выход 5x5. С помощью шага 2 мы получим выход 3x3. Давайте также посмотрим еще на один графический пример:

Иллюстрация пространственного расположения. В этом примере есть только одно пространственное измерение (ось x), один нейрон с размером рецептивного поля F = 3, входной размер W = 5 и нулевое заполнение P = 1. Сверху: Нейрон шагал по входу с шагом S = 1, давая на выходе размер (5 - 3 + 2)/1 + 1 = 5. Снизу: Нейрон использует шаг S = 2, давая выход размера (5 - 3 + 2)/2 + 1 = 3. Обратите внимание, что шаг S = 3 не может быть использован, так как он не будет аккуратно помещаться по объему. С точки зрения уравнения, это можно определить, так как (5 - 3 + 2) = 4 не делится на 3. Веса нейронов в этом примере [1,0,-1] (показаны справа), и их смещение равно нулю. Эти веса являются общими для всех желтых нейронов (см. общие параметры ниже).
Использование нулевой набивки. В приведенном выше примере слева обратите внимание, что входной размер был равен 5, а выходной размер был равен: также 5. Это сработало так, потому что наши рецептивные поля были равны 3, и мы использовали нулевую набивку 1. Если бы не использовалось заполнение нуля, то выходной объем имел бы пространственную размерность только 3, потому что именно столько нейронов «поместилось» бы на исходном входе. Как правило, установка нулевого заполнения равным P=(F−1)/2. Когда шаг S=1 гарантирует, что входной и выходной объем будут иметь одинаковый пространственный размер. Очень часто используется нулевое заполнение таким образом, и мы обсудим все причины, когда будем говорить больше об архитектурах ConvNet.
Ограничения на шаг. Обратите внимание, что гиперпараметры пространственного расположения имеют взаимные ограничения. Например, когда входные данные имеют размер W=10, нулевой отступ не используется P=0, а размер фильтра равен F=3, то использовать stride было бы невозможно S=2__с (W−F+2P)/S+1=(10−3+0)/2+1=4.5__, т.е. не целое число, указывающее на то, что нейроны не «помещаются» аккуратно и симметрично на входе. Таким образом, эта настройка гиперпараметров считается недопустимой, и библиотека ConvNet может выдать исключение или обнулить заполнение оставшейся части, чтобы она поместилась, или обрезать входные данные, чтобы она поместилась, или что-то еще. Как мы увидим в разделе Архитектуры ConvNet, правильный выбор размеров ConvNet, чтобы все размеры «отрабатывались», может стать настоящей головной болью, которую использование нулевого заполнения и некоторые рекомендации по проектированию значительно облегчат.
Пример из жизни. Архитектура Крижевского и др., которая выиграла конкурс ImageNet в 2012 году, принимала изображения размером [227x227x3]. На первом сверточном слое использовались нейроны с размером рецептивного поля F=11__шаг __S=4 и без нулевой набивки P=0. Так как (227 - 11)/4 + 1 = 55, и так как слой Conv имел глубину K=96 , выходной объем слоя Conv имел размер [55x55x96]. Каждый из 55x55x96 нейронов в этом объеме был соединен с областью размера [11x11x3] во входном объеме. Более того, все 96 нейронов в каждой глубинной колонке подключены к одной и той же области входного канала [11x11x3], но, конечно, с разными весами. В качестве забавного отступления, если вы прочитаете реальную статью, она утверждает, что входные изображения были 224x224, что, безусловно, неверно, потому что (224 - 11)/4 + 1 совершенно очевидно не является целым числом. Это сбило с толку многих людей в истории ConvNets, и мало что известно о том, что произошло. Мое собственное предположение заключается в том, что Алекс использовал нулевое заполнение из 3 дополнительных пикселей, о которых он не упоминает в статье.
Совместное использование параметров. Схема совместного использования параметров используется в сверточных слоях для управления количеством параметров. Используя приведенный выше пример из реальной жизни, мы видим, что в первом слое Conv 55 * 55 * 96 = 290 400 нейронов, и каждый из них имеет 11 * 11 * 3 = 363 веса и 1 смещение. В совокупности это дает 290400 * 364 = 105 705 600 параметров только на первом уровне ConvNet. Понятно, что это очень большое число.
Оказывается, что мы можем значительно сократить число параметров, если сделать одно разумное допущение: если один признак полезен для вычисления в некотором пространственном положении (x,y), то он также должен быть полезен для вычисления в другом положении (\(x_2, y_2\)). Другими словами, обозначив один двумерный срез глубины как срез глубины (например, объем размером [55x55x96] имеет 96 срезов глубины, каждый размером [55x55]), мы собираемся ограничить нейроны в каждом срезе глубины, чтобы они использовали одни и те же веса и смещение. При такой схеме распределения параметров первый слой Conv в нашем примере теперь будет иметь только 96 уникальных наборов весов (по одному для каждого среза глубины), что в сумме составит 96 * 11 * 11 * 3 = 34 848 уникальных весов, или 34 944 параметра (+96 смещений). В качестве альтернативы, все 55*55 нейронов в каждом срезе глубины теперь будут использовать одни и те же параметры. На практике во время обратного распространения каждый нейрон в объеме будет вычислять градиент для своих весов, но эти градиенты будут суммироваться для каждого среза глубины и обновлять только один набор весов для каждого среза.
Обратите внимание, что если все нейроны в одном срезе глубины используют один и тот же вектор весов, то прямой проход слоя CONV в каждом глубинном срезе может быть вычислен как свертка весов нейрона с входным объемом (отсюда и название: сверточный слой). Вот почему принято называть наборы весов фильтром (или ядром), который свертывается с входными данными.

Примеры фильтров, изученных Крижским и др. Каждый из 96 показанных здесь фильтров имеет размер [11x11x3], и каждый из них является общим для нейронов 55 * 55 в одном глубинном срезе. Обратите внимание, что предположение о совместном использовании параметров относительно разумно: если обнаружение горизонтального края важно в каком-то месте изображения, оно должно быть интуитивно полезным и в каком-то другом месте из-за трансляционно-инвариантной структуры изображений. Таким образом, нет необходимости заново учиться обнаруживать горизонтальный ребро в каждом из 55 * 55 различных мест в выходном объеме слоя Conv.
Обратите внимание, что иногда предположение о совместном использовании параметров может не иметь смысла. Это особенно верно в том случае, когда входные изображения в ConvNet имеют некоторую специфическую центрированную структуру, где мы должны ожидать, например, что на одной стороне изображения должны быть изучены совершенно разные функции, чем на другой. Одним из практических примеров является ситуация, когда входными данными являются лица, которые были центрированы на изображении. Можно ожидать, что различные особенности, специфичные для глаз или волос, могут (и должны) быть изучены в разных пространственных местах. В этом случае обычно ослабляют схему совместного использования параметров и вместо этого просто называют слой локально подключенным слоем.
Нумерные примеры. Чтобы сделать обсуждение выше более конкретным, давайте выразим те же идеи, но в коде и на конкретном примере. Предположим, что входной объем представляет собой массив numpy. Тогда:X
- Колонка глубины (или волокно) в позиции будет активацией.(x,y) X[x,y,:]
- Глубинным срезом или, что эквивалентноd, картой активации на глубине были бы активации X[:,:,d] .
Пример слоя conv. Предположим, что входной объем имеет форму . Предположим далее, что мы не используем нулевое заполнение (X X.shape: (11,11,4)P=0), что размер фильтра равен F=5, и что шаг является S=2. Таким образом, выходной объем будет иметь пространственный размер (11-5)/2+1 = 4, что дает объем с шириной и высотой 4. Карта активации в выходном объеме (назовем его ) будет выглядеть следующим образом (в этом примере вычисляются только некоторые элементы):V
- V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
- V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
- V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
- V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
Помните, что в numpy приведенная выше операция обозначает поэлементное умножение между массивами. Заметьте также, что вектор веса — это вектор веса этого нейрона и смещение. Здесь предполагается, что он имеет форму , так как размер фильтра равен 5, а глубина входного объема равна 4. Обратите внимание, что в каждой точке мы вычисляем скалярное произведение, как это было показано ранее в обычных нейронных сетях. Кроме того, мы видим, что мы используем тот же вес и смещение (из-за совместного использования параметров), и где размеры по ширине увеличиваются с шагом 2 (т.е. шаг). Чтобы построить вторую карту активации в выходном объеме, у нас есть:* W0 b0 W0 W0.shape: (5,5,4)
- V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
- V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
- V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
- V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
- V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (пример перехода по y)
- V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (или по обоим)
где мы видим, что мы индексируем второе измерение глубины в V (по индексу 1), потому что мы вычисляем вторую карту активации, и что теперь используется другой набор параметров (W1). В приведенном выше примере мы для краткости опускаем некоторые другие операции, которые Conv Layer выполнил бы для заполнения других частей выходного массива V. Кроме того, вспомните, что эти карты активации часто отслеживаются по элементам с помощью функции активации, такой как ReLU, но здесь это не показано.
Резюме. Подводя итог, можно сказать, что слой Conv:
- Принимает объем любого размера \(W_1 \times H_1 \times D_1\)
- Требуется четыре гиперпараметра:
- Количество фильтров K,
- их пространственная протяженность F,
- Шаг вперед S,
- Величина нулевого отступа P.
- Производит объем большого размера \(W_2 \times H_2 \times D_2\) где:
- W2=(W1−F+2P)/S+1
- H2=(H1−F+2P)/S+1 (т.е. ширина и высота вычисляются поровну по симметрии)
- D2=K
- Благодаря совместному использованию параметров он вводит \(F \cdot F \cdot D_1\) веса на фильтр, итого \((F \cdot F \cdot D_1) \cdot K\) веса и K cмещений.
- В выходном объеме метод d-я глубина среза (размера \(W_2 \times H_2\) ) является результатом выполнения валидной свертки d-й фильтр по входной громкости с шагом S, а затем сместить на d-ое смещение.
Общая настройка гиперпараметров выглядит следующим образом: F=3,S=1,P=1. Тем не менее, существуют общие условности и эмпирические правила, которые мотивируют эти гиперпараметры. Смотрите раздел Архитектуры ConvNet ниже.
Демо свертки. Ниже приведена бегущая демонстрация слоя CONV. Поскольку 3D-объемы трудно визуализировать, все объемы (входной объем (синий), весовой объем (красный), выходной объем (зеленый)) визуализируются с каждым срезом глубины, уложенным в ряды. Входной объем имеет размер \(W_1 = 5, H_1 = 5, D_1 = 3\), а параметры слоя CONV равны \(K = 2, F = 3, S = 2, P = 1\). То есть у нас есть два фильтра размера 3×3, и наносятся они с шагом 2. Следовательно, размер выходного объема имеет пространственный размер (5 - 3 + 2)/2 + 1 = 3. Кроме того, обратите внимание, что отступ P=1 применяется к входному объему, при этом внешняя граница входного объема обнуляется. На приведенной ниже визуализации перебираются выходные активации (зеленый) и показано, что каждый элемент вычисляется путем поэлементного умножения выделенных входных данных (синий) на фильтр (красный), суммирования его и последующего смещения результата.
- !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
-
- !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Реализация в виде умножения матриц. Обратите внимание, что операция свертки по сути выполняет скалярное произведение между фильтрами и локальными областями входных данных. Общий шаблон реализации слоя CONV заключается в том, чтобы воспользоваться этим фактом и сформулировать прямой проход сверточного слоя в виде умножения одной большой матрицы следующим образом:
_ Локальные регионы на входном изображении растягиваются в столбцы с помощью операции, обычно называемой im2col. Например, если входной параметр имеет размер [227x227x3] и он должен быть свернут с помощью фильтров 11x11x3 на шаге 4, то мы возьмем [11x11x3] блоков пикселей на входе и растянем каждый блок в вектор-столбец размером 11113 = 363. Повторение этого процесса на входе с шагом 4 дает (227-11)/4+1 = 55 позиций как по ширине, так и по высоте, что приводит к выходной матрице im2col размера [363 x 3025], где каждый столбец представляет собой растянутое восприимчивое поле, и всего их 55 x 55 = 3025. Обратите внимание, что поскольку рецептивные поля перекрываются, каждое число во входном объеме может дублироваться в нескольких отдельных столбцах.X_col
- Грузы слоя CONV аналогичным образом растягиваются в ряды. Например, если имеется 96 фильтров размера [11x11x3], то получится матрица размера [96 x 363]. W_row
- Результат свертки теперь эквивалентен выполнению одного умножения большой матрицы , которое вычисляет скалярное произведение между каждым фильтром и каждым местоположением восприимчивого поля. В нашем примере результатом этой операции будет [96 x 3025], что дает выходные данные скалярного произведения каждого фильтра в каждом месте.np.dot(W_row, X_col)
- В конечном итоге результат должен быть возвращен к его надлежащему выходному размеру [55x55x96].
У этого подхода есть недостаток, заключающийся в том, что он может использовать много памяти, так как некоторые значения во входном объеме многократно реплицируются в . Тем не менее, преимущество заключается в том, что существует множество очень эффективных реализаций матричного умножения, которыми мы можем воспользоваться (например, в широко используемом BLAS API). Более того, та же идея im2col может быть повторно использована для выполнения операции объединения, о которой мы поговорим далее.X_col
Обратное распространение. Обратный проход для операции свертки (как для данных, так и для весов) также является сверткой (но с пространственно перевернутыми фильтрами). Это легко вывести в одномерном случае с помощью примера с игрушкой (пока не раскрывается).
Свертка 1х1. В качестве отступления, в нескольких работах используются свертки 1x1, впервые исследованные Network in Network. Некоторые люди поначалу путаются, видя свертки 1x1, особенно когда они исходят из фона обработки сигналов. Обычно сигналы двумерны, поэтому свертки 1x1 не имеют смысла (это просто поточечное масштабирование). Однако в ConvNet это не так, потому что необходимо помнить, что мы работаем с трехмерными объемами и что фильтры всегда распространяются на всю глубину входного объема. Например, если входные данные равны [32x32x3], то выполнение сверток 1x1 фактически будет выполнением трехмерных скалярных произведений (поскольку глубина входных данных равна 3 каналам).
Расширенные извилины. Недавняя разработка (см., например, статью Фишера Ю. и Владлена Колтуна) заключается в введении еще одного гиперпараметра в слой CONV, называемого дилатацией. До сих пор мы обсуждали только непрерывные фильтры CONV. Тем не менее, можно иметь фильтры, которые имеют промежутки между каждой клеткой, называемые расширением. Например, в одном измерении фильтр размера 3 будет вычислять на входных данных следующее: . Это расширение до 0. Для расширения 1 фильтр вместо этого будет вычислять ; Другими словами, между заявками есть разрыв в 1. Это может быть очень полезно в некоторых настройках для использования в сочетании с фильтрами 0-расширения, поскольку это позволяет объединять пространственную информацию по входным данным гораздо более агрессивно с меньшим количеством слоев. Например, если вы наложите два слоя CONV 3x3 друг на друга, то вы можете убедить себя, что нейроны на втором слое являются функцией участка входного сигнала 5x5 (мы бы сказали, что эффективное рецептивное поле этих нейронов равно 5x5). Если мы будем использовать расширенные извилины, то это эффективное рецептивное поле будет расти гораздо быстрее.w x w[0]*x[0] + w[1]*x[1] + w[2]*x[2]w[0]*x[0] + w[1]*x[2] + w[2]*x[4]
Слой пула
В архитектуре ConvNet обычно периодически вставляется слой Pooling между последовательными слоями Conv. Его функция состоит в том, чтобы постепенно уменьшать пространственный размер представления для уменьшения количества параметров и вычислений в сети и, следовательно, также контролировать переобучение. Слой пулинга работает независимо на каждом срезе глубины входных данных и изменяет его пространственный размер с помощью операции MAX. Наиболее распространенной формой является пулинговый слой с фильтрами размером 2x2, применяемыми с шагом 2 вниздискретизации каждого глубинного среза на входе на 2 по ширине и высоте, отбрасывая 75% активаций. Каждая операция MAX в этом случае будет принимать максимум более 4 чисел (маленькая область 2x2 в некотором глубинном срезе). Размер глубины остается неизменным. В более общем смысле, пуловый слой: - Принимает объем любого размера W1×H1×D1 - Требуется два гиперпараметра: - их пространственная протяженность F, - Шаг вперед S, - Производит объем большого размера \(W_2 \times H_2 \times D_2\) где: - \(W_2 = (W_1 - F)/S + 1\) - \(H_2 = (H_1 - F)/S + 1\) - \(D_2 = D_1\) - Вводит нулевые параметры, так как вычисляет фиксированную функцию входных данных - Для слоев Pooling заполнение входных данных не является обычным способом с использованием нулевого отступа.
Стоит отметить, что на практике встречаются только два распространенных варианта максимального слоя пула: Слой пулинга с F=3,S=2 (также называемое перекрывающимся пулом) и чаще F=2,S=2. Объединение размеров с большими рецептивными полями слишком разрушительно.
Общий пул. В дополнение к максимальному объединению, единицы объединения могут выполнять и другие функции, такие как усредненное объединение или даже объединение по L2-норме. Исторически часто использовалось среднее объединение, но в последнее время оно вышло из моды по сравнению с операцией максимального объединения, которая, как было показано, работает лучше на практике.
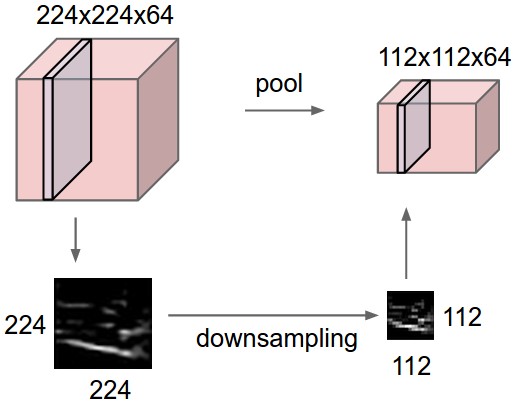
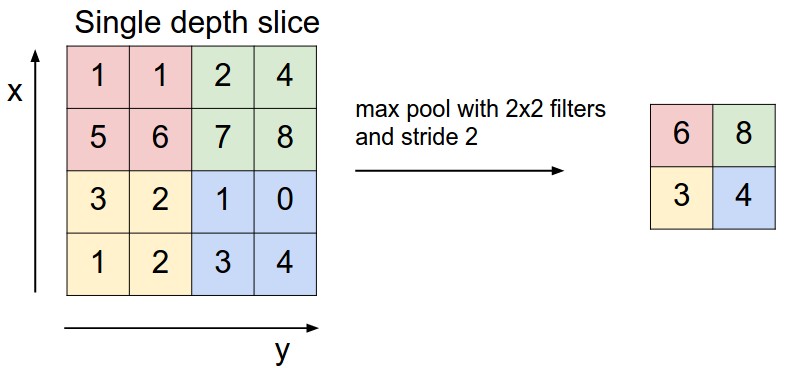
Пулинг слоя понижает дискретизацию объема пространственно, независимо в каждом глубинном срезе входного объема. Сверху: В этом примере входной объем размера [224x224x64] объединяется с фильтром размера 2, шаг 2 в выходной объем размера [112x112x64]. Обратите внимание, что глубина объема сохраняется. Снизу: Наиболее распространенной операцией понижения дискретизации является max, что приводит к максимальному объединению, показанному здесь с шагом 2. То есть, каждый макс берется над 4 числами (маленький квадратик 2х2).
Обратное распространение. Вспомните из главы об обратном распространении, что обратный проход для операции max(x, y) имеет простую интерпретацию как только маршрутизацию градиента на вход, который имел наибольшее значение в прямом проходе. Следовательно, во время прямого прохождения пулового слоя обычно отслеживают индекс максимальной активации (иногда также называемый переключателями), чтобы градиентная маршрутизация была эффективной во время обратного распространения.
Избавление от пулов. Многим людям не нравится операция по объединению, и они думают, что мы можем обойтись без нее. Например, Pursuit for Simplicity: The All Convolutional Net предлагает отказаться от пулового слоя в пользу архитектуры, состоящей только из повторяющихся слоев CONV. Чтобы уменьшить размер представления, они предлагают время от времени использовать больший шаг в слое CONV. Также было обнаружено, что отказ от слоев пула важен для обучения хороших генеративных моделей, таких как вариационные автоэнкодеры (VAE) или генеративно-состязательные сети (GAN). Вполне вероятно, что в будущих архитектурах будет очень мало или вообще не будет слоев пула.
Слой нормализации
Многие типы уровней нормализации были предложены для использования в архитектурах ConvNet, иногда с намерением реализовать схемы торможения, наблюдаемые в биологическом мозге. Однако с тех пор эти слои вышли из моды, потому что на практике их вклад был минимальным, если вообще был. О различных типах нормализации см. обсуждение в API библиотеки cuda-convnet Алекса Крижевского.
Полносвязный слой
Нейроны в полностью связном слое имеют полные связи со всеми активациями в предыдущем слое, как это видно в обычных нейронных сетях. Таким образом, их активации могут быть вычислены с помощью умножения матриц с последующим смещением смещения. Дополнительные сведения см. в разделе «Нейронные сети» примечаний.
Преобразование слоев FC в слои CONV
Стоит отметить, что единственное различие между слоями FC и CONV заключается в том, что нейроны в слое CONV связаны только с локальной областью на входе, и что многие нейроны в объеме CONV имеют общие параметры. Тем не менее, нейроны в обоих слоях по-прежнему вычисляют точечные произведения, поэтому их функциональная форма идентична. Таким образом, оказывается, что можно преобразовывать между слоями FC и CONV: - Для любого слоя CONV существует слой FC, реализующий ту же прямую функцию. Матрица весов будет большой матрицей, которая в основном равна нулю, за исключением некоторых блоков (из-за локальной связности), где веса во многих блоках равны (из-за совместного использования параметров). - И наоборот, любой слой FC может быть преобразован в слой CONV. Например, слой FC с K=4096, то есть с учетом некоторого входного объема размера 7×7×512 может быть эквивалентно выражен в виде слоя CONV с помощью F=7,P=0,S=1,K=4096. Другими словами, мы устанавливаем размер фильтра точно равным размеру входного объема, и, следовательно, на выходе будет просто 1×1×4096 так как только один столбец глубины «помещается» поперек входного объема, давая тот же результат, что и исходный слой FC.
Конверсия FC->CONV. Из этих двух преобразований возможность преобразования слоя FC в слой CONV особенно полезна на практике. Рассмотрим архитектуру ConvNet, которая берет изображение размером 224x224x3, а затем использует ряд слоев CONV и слоев POOL для уменьшения объема активации до размера 7x7x512 (в архитектуре AlexNet, которую мы увидим позже, это делается с помощью 5 слоев пула, которые каждый раз уменьшают пространственную дискретизацию входных данных в два раза). Получаем итоговый пространственный размер 224/2/2/2/2/2 = 7). После этого AlexNet использует два слоя FC размера 4096 и, наконец, последний слой FC с 1000 нейронами, которые вычисляют баллы класса. Мы можем преобразовать каждый из этих трех слоев FC в слои CONV, как описано выше: - Замените первый слой FC, который смотрит на объем [7x7x512], на слой CONV, использующий размер фильтра F=7, дающий выходной объем [1x1x4096]. - Замените второй слой FC на слой CONV, использующий размер фильтра F=1, дающий выходной объем [1x1x4096] - Замените последний слой FC аналогичным образом, на F=1, выдающий итоговый вывод [1x1x1000]
Каждое из этих преобразований на практике может включать в себя манипуляции (например, изменение формы) матрицей весов W в каждом слое FC в фильтры слоя CONV. Оказывается, что это преобразование позволяет нам очень эффективно «скользить» по исходной ConvNet через множество пространственных положений в более крупном изображении за один проход вперед.
Например, если образ 224x224 дает объем размера [7x7x512] - т.е. уменьшение на 32, то пересылка образа размера 384x384 через преобразованную архитектуру даст эквивалентный объем в размере [12x12x512], так как 384/32 = 12. Последующие 3 слоя CONV, которые мы только что преобразовали из слоев FC, теперь дадут окончательный объем размера [6x6x1000], поскольку (12 - 7)/1 + 1 = 6. Обратите внимание, что вместо одного вектора оценок классов размера [1x1x1000] мы теперь получаем целый массив оценок классов 6x6 на изображении 384x384.
Независимая оценка исходной ConvNet (со слоями FC) по кадрам 224x224 изображения 384x384 с шагом 32 пикселя дает результат, идентичный однократной пересылке преобразованной ConvNet.
Естественно, пересылка преобразованной ConvNet за один раз гораздо эффективнее, чем итерация исходной ConvNet по всем этим 36 местоположениям, поскольку 36 оценок используют общие вычисления. Этот трюк часто используется на практике для повышения производительности, когда, например, обычно изменяют размер изображения, чтобы сделать его больше, используют преобразованный ConvNet для оценки оценок класса во многих пространственных положениях, а затем усредняют баллы класса.
Наконец, что, если мы хотим эффективно применить исходную ConvNet поверх изображения, но с шагом меньше 32 пикселей? Мы могли бы добиться этого с помощью нескольких передач вперед. Например, обратите внимание, что если бы мы хотели использовать шаг в 16 пикселей, мы могли бы сделать это, объединив объемы, полученные при пересылке преобразованной ConvNet дважды: сначала над исходным изображением, а затем над изображением, но с пространственным сдвигом изображения на 16 пикселей как по ширине, так и по высоте.
- Блокнот IPython по сетевой хирургии показывает, как выполнить преобразование на практике, в коде (с использованием Caffe)
Архитектуры ConvNet
Мы видели, что сверточные сети обычно состоят только из трех типов слоев: CONV, POOL (мы предполагаем Max pool, если не указано иное) и FC (сокращение от fully connected). Мы также явно напишем функцию активации RELU в виде слоя, который применяет элементную нелинейность. В этом разделе мы обсудим, как они обычно складываются в целые ConvNet.
Узоры слоев
Наиболее распространенная форма архитектуры ConvNet состоит из нескольких слоев CONV-RELU, затем за ними следуют слои POOL и повторяет этот шаблон до тех пор, пока изображение не будет объединено в пространстве до небольшого размера. В какой-то момент часто происходит переход к полносвязным слоям. Последний полносвязный слой содержит выходные данные, такие как баллы класса. Другими словами, наиболее распространенная архитектура ConvNet следует шаблону:
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
где * указывает на повторение, а POOL? указывает на необязательный слой пула. Более того, N >= 0 (и обычно N <= 3 M >= 0 K >= 0), , (и обычно K < 3 ). Например, вот некоторые распространенные архитектуры ConvNet, которые следуют этому шаблону:
- INPUT -> FC реализует линейный классификатор. Здесь N = M = K = 0
- INPUT -> CONV -> RELU -> FC
- INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. Здесь мы видим, что между каждым слоем POOL есть один слой CONV.
-INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC. Здесь мы видим два слоя CONV, расположенных перед каждым слоем POOL. Как правило, это хорошая идея для более крупных и глубоких сетей, поскольку несколько слоев CONV могут привести к более сложным характеристикам входного объема перед деструктивной операцией объединения.
Отдайте предпочтение стеку небольших фильтров CONV одному большому слою рецептивного поля CONV. Предположим, что вы накладываете три слоя CONV 3x3 друг на друга (конечно, с нелинейностями между ними). При таком расположении каждый нейрон на первом слое CONV имеет представление входного объема 3x3. Нейрон на втором слое CONV имеет представление 3x3 первого слоя CONV и, следовательно, представление входного объема 5x5. Аналогично, нейрон на третьем слое CONV имеет представление 3x3 на 2-й слой CONV и, следовательно, на входной объем 7x7. Предположим, что вместо этих трех слоев 3x3 CONV мы хотим использовать только один слой CONV с рецептивными полями 7x7. Эти нейроны будут иметь размер рецептивного поля входного объема, идентичный в пространственном масштабе (7x7), но с некоторыми недостатками. - Во-первых, нейроны будут вычислять линейную функцию над входными данными, в то время как три стека слоев CONV содержат нелинейности, которые делают их особенности более выразительными. - Во-вторых, если мы предположим, что все тома имеют C каналов, то можно видеть, что один слой 7x7 CONV будет содержать \(C \times (7 \times 7 \times C) = 49 C^2\) параметры, в то время как три слоя 3x3 CONV будут содержать только \(3 \times (C \times (3 \times 3 \times C)) = 27 C^2\) параметры. Интуитивно понятно, что наложение слоев CONV с маленькими фильтрами в отличие от одного слоя CONV с большими фильтрами позволяет нам выразить более мощные функции входных данных с меньшим количеством параметров. В качестве практического недостатка нам может потребоваться больше памяти для хранения всех результатов промежуточного слоя CONV, если мы планируем использовать обратное распространение.
Недавние уходы. Следует отметить, что традиционная парадигма линейного списка слоев в последнее время была поставлена под сомнение в архитектурах Google Inception, а также в современных (современных) Residual Networks от Microsoft Research Asia. Оба они (см. подробности ниже в разделе тематических исследований) имеют более сложные и разные структуры подключения.
__На практике: используйте то, что лучше всего работает на ImageNet__. Если вы чувствуете некоторую усталость, думая об архитектурных решениях, вам будет приятно узнать, что в 90% или более приложений вам не нужно беспокоиться об этом. Я предпочитаю резюмировать этот момент как «не будьте героем» : вместо того, чтобы создавать свою собственную архитектуру для решения проблемы, вы должны посмотреть, какая архитектура в настоящее время лучше всего работает на ImageNet, загрузить предварительно обученную модель и настроить ее на основе ваших данных. В редких случаях приходится обучать ConvNet с нуля или проектировать его с нуля. Я также говорил об этом в школе Deep Learning.
Шаблоны для определения размеров слоев
До сих пор мы опускали упоминания об общих гиперпараметрах, используемых на каждом из уровней ConvNet. Сначала мы изложим общие эмпирические правила для определения размеров архитектур, а затем будем следовать правилам, обсуждая нотацию:
Входной слой (содержащий изображение) должен быть кратен 2 много раз. К распространенным номерам относятся 32 (например, CIFAR-10), 64, 96 (например, STL-10) или 224 (например, общие ImageNet ConvNet), 384 и 512.
Для конвальных слоев следует использовать небольшие фильтры (например, 3x3 или максимум 5x5), с шагом S=1 и, что особенно важно, заполнение входного объема нулями таким образом, чтобы слой conv не изменял пространственные размеры входных данных. То есть, когда F=3, то с помощью P=1 сохранит исходный размер входных данных. Когда F=5, P=2. Для генерала F, видно, что P=(F−1)/2 cохраняет размер ввода. Если вам нужно использовать фильтры большего размера (например, 7x7 или около того), это обычно можно увидеть только на самом первом выпуклом слое, который смотрит на входное изображение.
Слои пула отвечают за понижение дискретизации пространственных размеров входных данных. Наиболее распространенной настройкой является использование max-pooling с рецептивными полями 2x2 (т.е. F=2), и с шагом 2 (т.е. S=2). Обратите внимание, что при этом отбрасывается ровно 75% активаций входного объема (из-за уменьшения дискретизации на 2 раза как по ширине, так и по высоте). Другой, чуть менее распространенный вариант — использование рецептивных полей 3x3 с шагом 2, но это делает «подгонку» более сложной (например, слой 32x32x3 потребует нулевого заполнения для использования с максимальным объединением полей с рецептивным полем 3x3 и шагом 2). Очень редко можно увидеть, что размеры рецептивных полей для максимального пула больше 3, потому что в этом случае пулинг слишком потерян и агрессивен. Обычно это приводит к ухудшению производительности.
Уменьшение головной боли при уменьшении размера. Представленная выше схема радует тем, что все слои CONV сохраняют пространственный размер входных данных, в то время как только слои POOL отвечают за пространственное понижение объемов. В альтернативной схеме, где мы используем шаги больше 1 или не обнуляем входные данные в слоях CONV, нам пришлось бы очень тщательно отслеживать входные объемы по всей архитектуре CNN и убедиться, что все шаги и фильтры «работают» , и что архитектура ConvNet хорошо и симметрично связана.
Зачем использовать strace of 1 в CONV? Меньшие шаги лучше работают на практике. Кроме того, как уже упоминалось, шаг 1 позволяет нам оставить всю пространственную понижение дискретизации слоям POOL, при этом слои CONV преобразуют только входной объем по глубине.
Зачем использовать набивку? В дополнение к вышеупомянутому преимуществу сохранения постоянных пространственных размеров после CONV, это фактически повышает производительность. Если бы слои CONV не обнуляли входные данные, а выполняли только корректные свертки, то размер объемов уменьшался бы на небольшую величину после каждого CONV, а информация на границах «смывалась» бы слишком быстро.
Компрометация из-за ограничений памяти. В некоторых случаях (особенно на ранних этапах архитектуры ConvNet) объем памяти может очень быстро увеличиваться с помощью эмпирических правил, представленных выше. Например, фильтрация изображения размером 224x224x3 с тремя слоями CONV 3x3 с 64 фильтрами каждый и отступом 1 создаст три объема активации размером [224x224x64]. Это составляет в общей сложности около 10 миллионов активаций, или 72 МБ памяти (на изображение, как для активаций, так и для градиентов). Поскольку графические процессоры часто имеют узкие места из-за памяти, может потребоваться пойти на компромисс. На практике люди предпочитают идти на компромисс только на первом уровне CONV сети. Например, одним из компромиссов может быть использование первого слоя CONV с размерами фильтра 7x7 и шагом 2 (как в сети ZF). В качестве другого примера, AlexNet использует размеры фильтров 11x11 и stride 4.
Тематические исследования
В области сверточных сетей существует несколько архитектур, которые имеют название. Наиболее распространенными являются:
- LeNet. Первые успешные приложения сверточных сетей были разработаны Яном Лекуном в 1990-х годах. Из них наиболее известной является архитектура LeNet, которая использовалась для чтения почтовых индексов, цифр и т. д.
- AlexNet. Первой работой, которая популяризировала сверточные сети в компьютерном зрении, стала сеть AlexNet, разработанная Алексом Крижевским, Ильей Суцкевером и Джеффом Хинтоном. В 2012 году AlexNet был представлен на конкурс ImageNet ILSVRC и значительно превзошел занявшего второе место (ошибка в топ-5 16% по сравнению с ошибкой в 26%, занявшей второе место). Сеть имела очень похожую архитектуру на LeNet, но была глубже, больше и включала сверточные слои, наложенные друг на друга (ранее было обычным делом иметь только один слой CONV, за которым всегда следовал слой POOL).
- ZF Net. Победителем ILSVRC 2013 стала сверточная сеть от Мэтью Зейлера и Роба Фергуса. Она стала известна как ZFNet (сокращение от Zeiler & Fergus Net). Это было усовершенствование AlexNet за счет настройки гиперпараметров архитектуры, в частности, за счет увеличения размера средних сверточных слоев и уменьшения размера шага и фильтра на первом слое.
- GoogLeNet. Победителем ILSVRC 2014 стала сверточная сеть от Сегеди и др. от Google. Ее основным вкладом стала разработка модуля Inception, который значительно сократил количество параметров в сети (4M, по сравнению с AlexNet с 60M). Кроме того, в этой статье используется Average Pooling вместо Fully Connected layers в верхней части ConvNet, что устраняет большое количество параметров, которые не имеют большого значения. Существует также несколько последующих версий GoogLeNet, последняя из которых Inception-v4.
- VGGNet. Второе место на ILSVRC 2014 заняла сеть Карена Симоняна и Эндрю Зиссермана, которая стала известна как VGGNet. Его основной вклад заключался в том, что он показал, что глубина сети является критически важным компонентом для хорошей производительности. Их окончательная лучшая сеть содержит 16 слоев CONV/FC и, что привлекательно, отличается чрезвычайно однородной архитектурой, которая выполняет только свертки 3x3 и пул 2x2 от начала до конца. Их предварительно обученная модель доступна для использования в Caffe по принципу «подключи и работай». Недостатком VGGNet является то, что он дороже в оценке и использует гораздо больше памяти и параметров (140M). Большинство этих параметров находятся в первом полностью связанном слое, и с тех пор было обнаружено, что эти слои FC могут быть удалены без снижения производительности, что значительно сокращает количество необходимых параметров.
- ResNet.. Остаточная сеть, разработанная Каим Хе и др., стала победителем ILSVRC 2015. Она оснащена специальными соединениями для пропуска и интенсивным использованием пакетной нормализации. В архитектуре также отсутствуют полностью связанные слои в конце сети. Читателю также предлагается ознакомиться с презентацией Кайминга (видео, слайды) и некоторыми недавними экспериментами, которые воспроизводят эти сети в Torch. В настоящее время ResNet являются самыми современными моделями сверточных нейронных сетей и являются выбором по умолчанию для использования ConvNet на практике (по состоянию на 10 мая 2016 года). В частности, см. более поздние разработки, которые корректируют исходную архитектуру, из книги Каим Хе и др. IСопоставления идентификационных данных в глубоких остаточных сетях (опубликована в марте 2016 г.).
VGGNet в деталях. Давайте разберем VGGNet более подробно в качестве тематического исследования. Вся сеть VGGNet состоит из слоев CONV, которые выполняют свертки 3x3 со stride 1 и pad 1, и из слоев POOL, которые выполняют 2x2 max pooling с stride 2 (и без отступа). Мы можем записывать размер представления на каждом шаге обработки и отслеживать как размер представления, так и общее количество весов:
INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters
Как и в случае со сверточными сетями, обратите внимание, что большая часть памяти (а также вычислительного времени) используется в ранних слоях CONV, а большинство параметров — в последних слоях FC. В данном конкретном случае первый слой FC содержит 100 м грузов из общего числа 140 м.
Вычислительные соображения
Самым большим узким местом, о котором следует знать при создании архитектур ConvNet, является узкое место памяти. Многие современные графические процессоры имеют ограничение в 3/4/6 ГБ памяти, а лучшие графические процессоры имеют около 12 ГБ памяти. Существует три основных источника памяти, которые необходимо отслеживать:
- Из промежуточных размеров объемов: Это исходное количество активаций на каждом уровне ConvNet, а также их градиенты (одинакового размера). Как правило, большая часть активаций происходит на более ранних уровнях ConvNet (т.е. на первых уровнях Conv). Они сохраняются, потому что они нужны для обратного распространения, но умная реализация, которая запускает ConvNet только во время тестирования, в принципе могла бы значительно сократить это, сохраняя только текущие активации на любом уровне и отбрасывая предыдущие активации на уровнях ниже.
- Из размеров параметров: Это числа, которые содержат параметры сети, их градиенты во время обратного распространения и, как правило, также кэш шагов, если оптимизация выполняется с использованием momentum, Adagrad или RMSProp. Следовательно, память для хранения только вектора параметров обычно должна быть умножена по крайней мере на 3 или около того.
- Каждая реализация ConvNet должна поддерживать различную память, такую как пакеты данных изображений, возможно, их дополненные версии и т.д.
После того, как вы получили приблизительную оценку общего количества значений (для активаций, градиентов и разного), это число следует преобразовать в размер в ГБ. Возьмите количество значений, умножьте на 4, чтобы получить исходное количество байтов (поскольку каждая плавающая точка равна 4 байтам, или, возможно, на 8 для двойной точности), а затем разделите на 1024 несколько раз, чтобы получить объем памяти в КБ, МБ и, наконец, в ГБ. Если ваша сеть не подходит, обычной эвристикой для «подгонки» является уменьшение размера пакета, поскольку большая часть памяти обычно потребляется активациями.
Дополнительные материалы
Дополнительные ресурсы, связанные с реализацией:
- Бенчмарки Soumith для производительности CONV
- Демонстрация ConvNetJS CIFAR-10 позволяет экспериментировать с архитектурами ConvNet и видеть результаты и вычисления в режиме реального времени, в браузере.
- Caffe, одна из популярных библиотек ConvNet.
- Современные ResNet в Torch7