Основы трехмерного компьютерного зрения
1. Введение
Камера является одним из важнейших инструментов в компьютерном зрении. Это механизм, с помощью которого мы можем фиксировать окружающий мир и использовать получаемые результаты — фотографии — для различных приложений. Поэтому один из фундаментальных вопросов трехмерного компьютерного зрения звучит так: как мы можем смоделировать камеру?
2. Камера-обскура
Камера-обскура — это простейшая система, которая позволяет фиксировать изображение объекта или сцены в трёхмерном мире. Такая система может быть создана путём размещения преграды с небольшим отверстием (апертурой) между трёхмерным объектом и фотоплёнкой или светочувствительным сенсором.
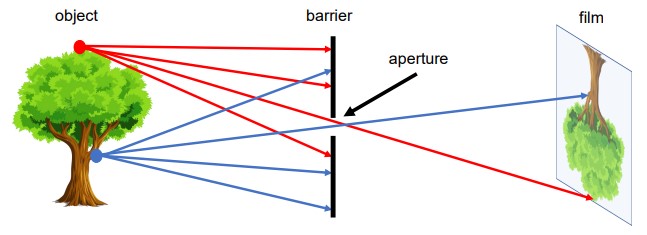
Рисунок 1: Модель камеры обскуры
Как показано на рисунке 1, каждая точка на трёхмерном объекте испускает множество световых лучей во все стороны. Без преграды каждая точка на плёнке подвергалась бы воздействию световых лучей, исходящих от каждой точки трёхмерного объекта. Благодаря наличию преграды через отверстие проходит только один (или несколько) из этих лучей света и попадает на плёнку.
Таким образом, мы можем установить взаимно-однозначное соответствие между точками на трёхмерном объекте и точками на плёнке. В результате плёнка получает «изображение» трёхмерного объекта посредством такого отображения. Эта простая модель известна как модель камеры-обскуры.
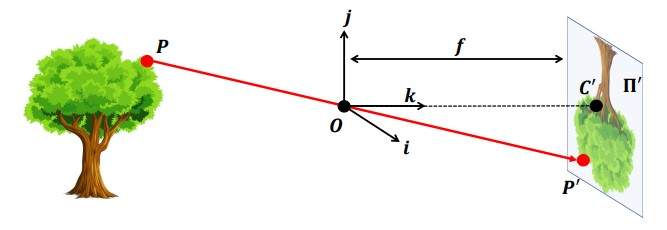
Рисунок 2: Формальная модель камеры-обскуры
Более формальное построение камеры-обскуры показано на рисунке 2. В этой конструкции плёнка обычно называется плоскостью изображения или сетчаткой. Отверстие называется точечным отверстием O или центром камеры. Расстояние между плоскостью изображения и точечным отверстием O называется фокусным расстоянием f.
Иногда плоскость сетчатки размещается между точкой O и трёхмерным объектом на расстоянии f от O. В этом случае она называется виртуальной плоскостью изображения или виртуальной плоскостью сетчатки. Важно отметить, что проекция объекта на плоскость изображения и изображение объекта на виртуальной плоскости изображения идентичны с точностью до масштабного (подобного) преобразования.
Теперь рассмотрим, как использовать камеры-обскуры. Пусть $P = [x y z]^T$ — точка на некотором трёхмерном объекте, видимом для камеры-обскуры. Точка $P$ будет отображена или спроецирована на плоскость изображения $Π'$, в результате чего получится точка $P' = [x' y']^T$.
Аналогично, само точечное отверстие может быть спроецировано на плоскость изображения, что даст новую точку $C'$. Здесь мы можем определить трехмерную систему координат $[i j k]$ с центром отсчета в точке отверстия $O$. Ось k перпендикулярна плоскости изображения и направлена к ней. Эта система координат известна как система координат камеры.
Линия, определяемая точками C' и O, называется оптической осью системы камеры.
Напомним, что точка $P_0$ получается в результате проекции трёхмерной точки $P$ на плоскость изображения $Π'$. Следовательно, если мы выведем соотношение между трёхмерной точкой $P$ и точкой $P'$ на плоскости изображения, мы сможем понять, как трёхмерный мир отображается на снимке, сделанном камерой-обскурой.
Обратите внимание, что треугольник $P' C'O$ подобен треугольнику, образованному точками $P$, $O$ и $(0, 0, z)$. Используя теорему о подобных треугольниках, мы получаем:
$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{fx}{z} \\ \frac{fy}{z} \end{pmatrix}$ (1)
Важно отметить, что в этой модели камеры-обскуры мы делаем одно существенное допущение: апертура (отверстие) считается одной точкой. Однако в большинстве реальных ситуаций мы не можем предполагать, что апертура может быть бесконечно малой. Возникает вопрос: как влияет изменение размера апертуры на результат?
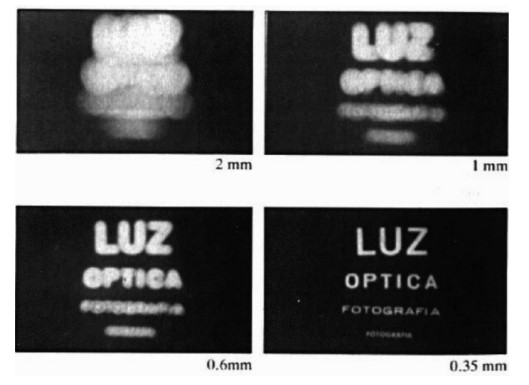
Рисунок 3: Влияние размера апертуры на изображение
При уменьшении размера апертуры изображение становится более резким, но более тёмным.
По мере увеличения размера апертуры количество световых лучей, проходящих через преграду, соответственно возрастает. При большем количестве проходящих лучей каждая точка на плёнке может подвергаться воздействию световых лучей от нескольких точек в трёхмерном пространстве, что приводит к размытию изображения.
Хотя может показаться заманчивым сделать апертуру как можно меньше, следует помнить, что меньший размер апертуры пропускает меньше световых лучей, в результате чего изображение получается более чётким, но более тёмным.
Таким образом, мы приходим к фундаментальной проблеме, возникающей при использовании камеры-обскуры: возможно ли создать камеру, которая делает одновременно чёткие и яркие изображения?
3. Камеры и линзы
В современных камерах указанное противоречие между резкостью и яркостью изображения решается с помощью линз — устройств, способных фокусировать или рассеивать свет.
Если заменить отверстие (апертуру) камеры-обскуры на линзу, которая правильно расположена и имеет подходящий размер, то она будет обладать следующим свойством: все световые лучи, испускаемые некоторой точкой $P$, преломляются линзой таким образом, что они сходятся в одной точке $P'$.
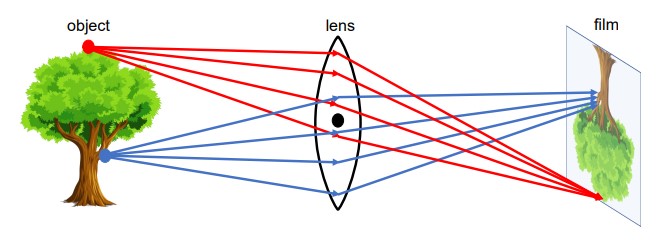
Рисунок 4: Схема простой модели линзы
На рисунке 4 показано, как лучи от верхней точки дерева хорошо сходятся на плёнке. Однако точка, находящаяся на другом расстоянии от линзы, приводит к тому, что лучи не сходятся идеально на плёнке.
Благодаря линзе проблема блокировки большинства световых лучей из-за малого отверстия устраняется (см. рисунок 4). Однако важно отметить, что это свойство выполняется не для всех точек трёхмерного пространства, а только для определённой точки $P$.
Рассмотрим другую точку $Q$, которая находится ближе или дальше от плоскости изображения, чем точка $P$. Соответствующая проекция на изображение будет размытой или не в фокусе. Таким образом, у линз есть определённое расстояние, на котором объекты находятся «в фокусе». Эффективный диапазон, в пределах которого камеры могут делать чёткие снимки называется глубина резкости.
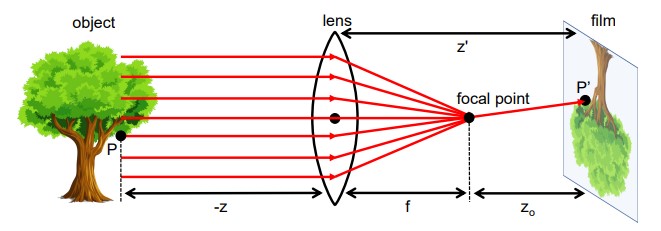
Рисунок 5: Фокусировка световых лучей с помощью линзы
На данном рисунке демонстрируется, как линза фокусирует световые лучи, параллельные оптической оси, в фокусе (фокальной точке). Эта схема также иллюстрирует модель параксиального преломления — упрощённую модель, которая помогает установить взаимосвязь между точками на плоскости изображения и объектами в трёхмерном пространстве для камер с линзами.
Параксиальное преломление — это приближение, используемое в оптике, которое позволяет:
- точно рассчитывать траектории световых лучей;
- определять положение точек в пространстве;
- вычислять параметры фокусировки;
- моделировать работу оптических систем.
Такая модель является фундаментальной для понимания принципов работы современных камер и систем компьютерного зрения.
Объективы камер обладают ещё одним важным свойством: они фокусируют все световые лучи, движущиеся параллельно оптической оси, в одну точку, известную как фокусная точка (см. рисунок 5). Расстояние между фокусной точкой и центром линзы называется фокусным расстоянием $f$.
Кроме того, световые лучи, проходящие через центр линзы, не отклоняются. Благодаря этому мы можем построить конструкцию, аналогичную модели камеры-обскуры, которая связывает точку $P$ в трёхмерном пространстве с соответствующей точкой $P'$ на плоскости изображения:
$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} z' \frac{x}{z} \\ z' \frac{y}{z} \end{pmatrix}$ (2)
Важно отметить следующие различия между моделями:
- В модели камеры-обскуры $z' = f$
- В модели с линзой $z' = f + z_0$
Данное соотношение основано на параксиальном приближении (или предположении о «тонкой линзе»), а такая модель называется моделью параксиального преломления. Подробное доказательство этой модели выходит за рамки данного курса.
Поскольку модель параксиального преломления использует приближение тонкой линзы, может возникать ряд аберраций. Наиболее распространённой из них является радиальное искажение, которое приводит к уменьшению или увеличению увеличения изображения в зависимости от расстояния до оптической оси.
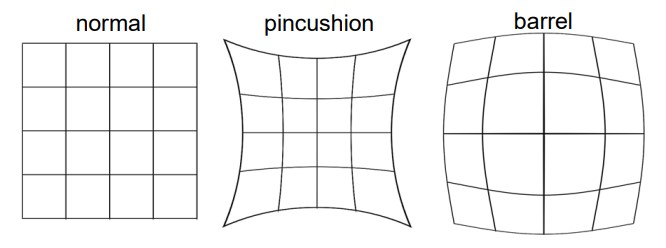
Рисунок 6: Подушкообразное и бочкообразное искажение изображения
Мы классифицируем радиальное искажение следующим образом:
- Подушкообразное искажение — когда увеличение возрастает
- Бочкообразное искажение — когда увеличение уменьшается.
Радиальное искажение возникает из-за того, что различные участки линзы имеют разные фокусные расстояния. Это явление наглядно показано на рисунке 6, где можно увидеть, как эти типы искажений влияют на конечное изображение.
Такие искажения особенно заметны:
- По краям кадра
- При использовании широкоугольных объективов
- В системах компьютерного зрения, где важна точность геометрических измерений
4. Матричная модель камеры
В этом разделе мы рассмотрим детали параметров, которые необходимо учитывать при моделировании проекции из трёхмерного пространства на известные нам цифровые изображения. Все полученные результаты будут использовать модель камеры-обскуры, но они также применимы и к модели параксиального преломления.
Как обсуждалось ранее, точка $P$ в трёхмерном пространстве может быть отображена (или спроецирована) в двумерную точку $P'$ на плоскости изображения $Π'$. Такое отображение $R^3 → R^2$ называется проективным преобразованием.
Однако такая проекция трёхмерных точек на плоскость изображения не соответствует напрямую тому, что мы видим в реальных цифровых изображениях по нескольким причинам:
- Точки в цифровых изображениях, как правило, находятся в другой системе отсчёта, чем точки в плоскости изображения.
- Цифровые изображения разделены на дискретные пиксели, тогда как точки в плоскости изображения являются непрерывными.
- Физические датчики могут вносить нелинейные искажения в отображение.
Чтобы учесть эти различия, мы введём ряд дополнительных преобразований, которые позволят нам отображать любую точку из трёхмерного мира в координаты пикселей.
Таким образом, нам необходимо:
- Учесть различия в системах координат;
- Преобразовать непрерывные координаты в дискретные пиксельные;
- Компенсировать возможные искажения сенсора.
Матричная модель камеры описывает набор важных параметров, влияющих на то, как точка мира $P$ отображается в координаты изображения $P'$. Как следует из названия, эти параметры представлены в матричной форме.
Рассмотрим основные параметры:
Параметры $c_x$ и $c_y$ описывают смещение между координатами плоскости изображения и цифровыми координатами изображения через перенос.
- Координаты плоскости изображения имеют начало координат $C_0$ в центре изображения, где ось $k$ пересекает плоскость изображения.
- Цифровые координаты изображения обычно имеют начало в левом нижнем углу изображения.
- Таким образом, 2D точки на плоскости изображения и 2D точки в цифровом изображении смещаются на вектор переноса $\begin{pmatrix} c_x \\ c_y \end{pmatrix}^T$.
С учётом этого изменения систем координат, проективное отображение точки имеет следующий вид:
$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{f}{z}x + c_x \\ \frac{f}{z}y + c_y \end{pmatrix}$ (3)
Второй важный эффект — это то, что точки в цифровых изображениях выражаются в пикселях, в то время как точки на плоскости изображения представлены в физических единицах измерений (метрах).
Для учёта этого изменения единиц измерения необходимо ввести два новых параметра $k$ и $l$. Эти параметры имеют размерность [пиксель / милиметр], по двум осям плоскости изображения. Важно отметить, что $k$ и $l$ могут иметь разные значения, поскольку соотношение сторон пикселя не обязательно равно единице. Если $k = l$, мы говорим, что камера имеет квадратные пиксели.
С учетом этого, отображение выглядит следующим образом:
$P_0 = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} f k \frac{x}{z} + c_x \\ f l \frac{y}{z} + c_y \end{pmatrix} = \begin{pmatrix} \alpha\frac{x}{z} + c_x \\ \beta\frac{y}{z} + c_y \end{pmatrix}$ (4)
где
$\alpha = f \cdot k$
$\beta = f \cdot l$
$f$ — фокусное расстояние в мм,
$k$ — размер пикселя по оси x, пикс/мм.
$l$ — размер пикселя по оси x, пикс/мм.
Сокращение размерностей приводит к тому, что параметры $\alpha$ и $\beta$ выражаются в пикселях.
Это логично, так как коэффициенты связывают физические измерения (метры) с дискретными единицами цифрового изображения (пиксели).
Геометрический смысл параметров $\alpha$ и $\beta$ состоит в том, сколько пикселей будет занимать объект, размер которого на плоскости проекции равен фокусному расстоянию камеры.
Таким образом, измерение $\alpha$ и $\beta$ в пикселях является необходимым для работы алгоритмов обработки изображений и взаимосвязи между физическим и цифровым пространством.
5. Однородные координаты
Из уравнения (4) видно, что проецирование $P \rightarrow P'$ не является линейным, поскольку операция включает деление на один из входных параметров, а именно на $z$.
Однако на практике гораздо удобне работать с линейными преобразованиями, т.к. их можно представить как произведение входного вектора $P$ на некоторую матрицу.
Существует ли линейный способ представления проецирования $P \rightarrow P'$ ?
Ответ - да, представление этого проецирования в виде произведения вектора на матрицу возможно.
Решение заключается в использовании однородных координат.
Рассмотрим этот подход:
Введение новой координаты:
Любая точка на плоскости $P' = (x', y')$ преобразуется в $(x', y', 1)$
Любая точка в трехмерном пространстве $P = (x, y, z)$ преобразуется в $(x, y, z, 1)$
Такое расширенное пространство называется системой однородных координат.
Преобразование координат:
Для преобразования евклидова вектора $(v_1, ..., v_n)$ в однородные координаты мы просто добавляем 1 в новое измерение, получая $(v_1, ..., v_n, 1)$ Важно отметить, что равенство между вектором и его однородными координатами выполняется только когда последняя координата равна единице. При обратном преобразовании из произвольных однородных координат $(v_1, ..., v_n, w)$ мы получаем евклидовы координаты $(\frac{v_1}{w}, ..., \frac{v_n}{w})$
Используя однородные координаты, мы можем сформулировать преобразование следующим образом:
$P'_h = \begin{bmatrix} \alpha x + c_x z \\ \beta y + c_y z \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P_h$ (5)
Основным преимуществом использования однородных координат является то, что они позволяют представить нелинейное преобразование в виде матричного умножения. Это упрощает дальнейшие математические выкладки и обеспечивает единый способ работы с проективными преобразованиями.
В дальнейшем мы будем работать преимущественно в однородных координатах, если не указано иное. Индекс $h$ опустим, подразумевая, что любая точка $P$ или $P'$ задана в однородных координатах.
Как видно из уравнения (5), можно представить связь между точкой в трёхмерном пространстве и её координатами изображения в виде матрично-векторного соотношения:
$P' = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P = MP$ (6)
где:
- $M$ — матрица камеры
- $P$ — точка в однородных координатах трёхмерного пространства
- $P'$ — проекция точки на плоскость изображения
6. Внутренние параметры камеры
Важные параметры матрицы камеры:
- $\alpha$ и $\beta$ — масштабные коэффициенты в направлениях $x$ и $y$
- $c_x$ и $c_y$ — координаты главной точки (principal point)
Последний столбец матрицы $M$ содержит нули, что характерно для проективных преобразований.
Давайте разберем это матричное разложение более подробно:
Мы можем представить преобразование в виде:
$P' = MP = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} I & 0 \end{bmatrix} P = K \begin{bmatrix} I & 0 \end{bmatrix} P$ (7)
где:
- $P'$ — координаты точки на плоскости изображения
- $M$ — полная матрица преобразования
- $K$ — *матрица камеры- (внутренняя калибровка)
- $I$ — единичная матрица размером 3×3
- $0$ — нулевой вектор размером 3×1
- $P$ — координаты точки в пространстве в однородных координатах.
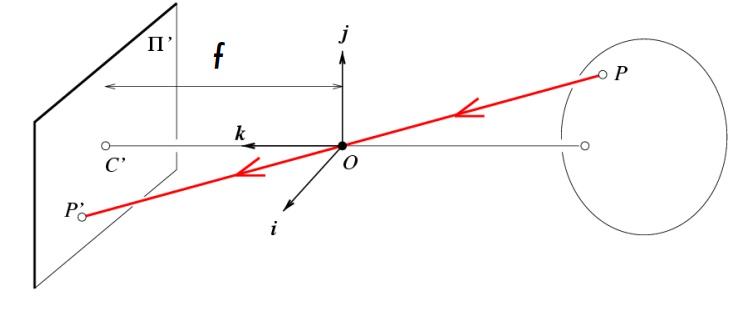
Рисунок 7: Проекция точки с помощью матрицы камеры
Матрица камеры $K$ имеет следующий вид:
$K = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix}$
где:
- $\alpha$ и $\beta$ — масштабные коэффициенты, связанные с фокусным расстоянием;
- $c_x$ и $c_y$ — координаты главной точки (principal point).
Последняя строка [0 0 1] обеспечивает сохранение однородных координат.
Матрица $K$ содержит всю необходимую информацию об внутренней калибровке камеры, что делает её ключевым элементом в задачах компьютерного зрения и обработки изображений.
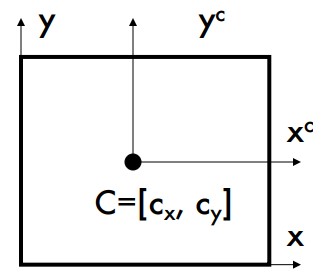
Рисунок 8: Расположение главной точки С'
Полная матричная модель камеры $K$ содержит ключевые параметры $c_x$, $c_y$, $k$ и $l$. Однако в текущей формулировке отсутствуют два важных параметра: скос (skewness) и дисторсия (distortion).
Скос изображения возникает, когда система координат камеры имеет неточный угол между осями (отличающийся от 90 градусов). Большинство камер имеют нулевой скос, однако некоторое его значение может появиться из-за погрешностей при производстве сенсора.
Матрица камеры с учётом скоса имеет вид:
$K = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & -\alpha \cot \theta & c_x \\ 0 & \frac{\beta}{\sin \theta} & c_y \\ 0 & 0 & 1 \end{bmatrix}$ (8)
где:
- $\alpha$ и $\beta$ — масштабные коэффициенты
- $\theta$ — угол скоса
- $c_x$ и $c_y$ — координаты главной точки
Очень часто рассматривается матрица камеры $K$ с 5 степенями свободы:
- 2 параметра для фокусного расстояния;
- 2 параметра для смещения;
- 1 параметр для скоса.
Однако большинство методов компьютерного зрения игнорируют эффекты дисторсии, позволяя состедоточиться на 4 основных параметрах камеры.
7. Внешние параметры камеры
До сих пор мы описывали отображение точки $P$ из трёхмерной системы координат камеры в точку $P'$ на двумерной плоскости изображения, используя внутренние параметры камеры в матричной форме.
Однако возникает вопрос: что делать, если информация о трёхмерном мире представлена в другой системе координат? В этом случае необходимо добавить дополнительное преобразование, связывающее точки из мировой системы координат с системой координат камеры.
Это преобразование описывается:
- Матрицей вращения $R$
- Вектором переноса $T$
Таким образом, для точки $P_w$ в мировой системе координат её координаты в системе камеры можно вычислить следующим образом:
$P = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} P_w$ (9)
где:
- $R$ — матрица вращения размером 3×3
- $T$ — вектор переноса размером 3×1
- $P_w$ — координаты точки в мировой системе
- $P$ — координаты точки в системе камеры
Подставляя это в уравнение (7) и упрощая, получаем:
$P' = K \begin{bmatrix} R & T \end{bmatrix} P_w = MP_w$ (10)
Параметры $R$ и $T$ называются внешними параметрами, поскольку они определяют положение и не зависят от внутренних характеристик камеры.
Резюме
Полная матрица проекции $M$ состоит из двух типов параметров:
- Внутренние параметры (intrinsic parameters) — содержатся в матрице камеры $K$, меняются при смене типа камеры
- Внешние параметры (extrinsic parameters) — включают вращение и перенос, не зависят от конструкции камеры
Полная матрица проекции $M$ размером 3×4 имеет 11 степеней свободы:
- 5 степеней свободы внутренней матрицы камеры;
- 3 степени свободы внешнего вращения;
- 3 степени свободы внешнего переноса.
Таким образом, мы получили полное описание процесса проецирования точки из трёхмерного пространства на плоскость изображения. При этом мы учитываем как характеристики самой камеры, так и её положение в пространстве относительно наблюдаемой сцены.