Калибровка камеры
1. Калибровка камеры
Преобразование объектов из реального трёхмерного мира в цифровые изображения требует знания параметров камеры. В общем случае мы можем как иметь доступ к этим параметрам, так и не иметь его. Однако мы можем вычислить параметры из тех изображений, которые сделаны с помощью этой камеры.
Задача оценки внешних и внутренних параметров камеры известна как калибровка камеры.
Калибровка камеры — это фундаментальный процесс в компьютерном зрении и обработке изображений, который позволяет нам переходить от наблюдаемых пикселей к реальным координатам в пространстве.
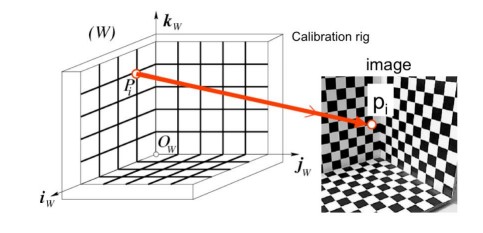
Рисунок 1: Пример калибровочной установки
Процесс калибровки камеры заключается в определении внутренней матрицы камеры $K$ и внешних параметров $R$, $T$ из уравнения (1).
$P' = K \begin{bmatrix} R & T \end{bmatrix} P_w = MP_w$ (1)
Рассмотрим этот процесс в контексте калибровочной установки, показанной на рисунке 1.
Калибровочная установка обычно состоит из простого шаблона (например, шахматной доски) с известными размерами. Кроме того, установка определяет мировую систему координат с началом $O_w$ и осями $i_w$, $j_w$, $k_w$.
Из известного шаблона мы получаем точки в мировой системе координат $P_1, ..., P_n$. Найдя эти точки на изображении, полученном с камеры, мы получаем соответствующие точки изображения $p_1, ..., p_n$.
Мы составляем линейную систему уравнений из $n$ соответствий, $P_i$, $p_i$ и матрицы камеры $M$, которая состоит из строк $m_1$, $m_2$, $m_3$:
$p_i = \begin{pmatrix} u_i \\ v_i \end{pmatrix} = MP_i = \begin{pmatrix} \frac{m_1P_i}{m_3P_i} \\ \frac{m_2P_i}{m_3P_i} \end{pmatrix}$ (2)
Уравнение (2) даёт нам два ограничения для нахождения неизвестных параметров, содержащихся в векторах $m$.
Мы знаем, что матрица камеры имеет 11 неизвестных параметров (6 внешних и 5 внутренних). Это означает, что нам нужно как минимум 6 соответствий для решения. Однако в реальном мире мы часто используем больше соответствий, поскольку измеренные координаты содержат шумы и погрешности.
Для каждой точки $P_i$ мы можем вывести пару уравнений, связывающих координаты на плоскости $u_i, v_i$ с 3D координатами:
$u_i(m_3P_i) − m_1P_i = 0$
$v_i(m_3P_i) − m_2P_i = 0$
При наличии $n$ таких соответствующих точек вся линейная система уравнений принимает вид:
$u_1(m_3P_1)−m_1P_1 = 0$
$v_1(m_3P_1)−m_2P_1 = 0$
...
$u_n(m_3P_n)−m_1P_n = 0$
$v_n(m_3P_n)−m_2P_n = 0$
Мы можем вынести вектора $m_1 , m_2, m_3$ и представить эту систему уравнений в виде матричного произведения:
$\begin{bmatrix} P_1 & 0 & -u_1P_1 \\ 0 & P_1 & -v_1P_1 \\ \vdots & \vdots & \vdots \\ P_n & 0 & -u_nP_n \\ 0 & P_n & -v_nP_n \end{bmatrix} \begin{bmatrix} m_1 \\ m_2 \\ m_3 \end{bmatrix} = Pm = 0$ (3)
Когда $2n > 11$, наша однородная линейная система является переопределённой. Для такой системы $m = 0$ всегда является тривиальным решением. Более того, даже если существует ненулевое решение $m$, то для любого $\rho \in \mathbb{R}$, $km$ также будет решением.
Поэтому для ограничения решения мы выполняем следующую минимизацию:
$\min_{m} |Pm|^2 \quad \text{при условии} \quad |m|^2 = 1$ (4)
Для решения этой задачи минимизации используется сингулярное разложение. Если обозначить $P = UDV^T$, то решение задачи минимизации заключается в том, чтобы установить $m$ равным последнему столбцу матрицы $V$. За доказательством данного решения можно обратиться к разделу 5.3 книги Hartley & Zisserman стр. 592–593.
После преобразования вектора $m$ в матрицу $M$ мы хотим найти внешние и внутренние параметры камеры.
C помощью SVD мы вычислили матрицу $M$, с точностью до масштабного множителя $\rho$.
$\rho M = \begin{bmatrix} \alpha r_1^T - \alpha \cot \theta r_2^T + c_x r_3^T & \alpha t_x - \alpha \cot \theta t_y + c_x t_z \\ \frac{\beta}{\sin \theta} r_2^T + c_y r_3^T & \frac{\beta}{\sin \theta} t_y + c_y t_z \\ r_3^T & t_z \end{bmatrix}$ (5)
где $r_1^T$, $r_2^T$, и $r_3^T$ — это три строки матрицы вращения $R$.
Разделим на скаляр $\rho$ и обозначим первый столбец как матрицу $A$, а второй столбец как вектор $b$:
$M = \frac{1}{\rho} \begin{bmatrix} \alpha r_1^T - \alpha \cot \theta r_2^T + c_x r_3^T & \alpha t_x - \alpha \cot \theta t_y + c_x t_z \\ \frac{\beta}{\sin \theta} r_2^T + c_y r_3^T & \frac{\beta}{\sin \theta} t_y + c_y t_z \\ r_3^T & t_z \end{bmatrix} = \begin{bmatrix} A & b \end{bmatrix} = \begin{bmatrix} a_1^T & b_1 \\ a_2^T & b_2 \\ a_3^T & b_3 \end{bmatrix}$
Теперь мы можем вычислить внутренние параметры камеры через элементы известной матрицы $M$, она же $A$ и $b$: (6)
Масштабный множитель:
$\rho = \pm \frac{1}{|a_3|}$
Координаты главной точки:
$c_x = \rho^2 (a_1 \cdot a_3)$
$c_y = \rho^2 (a_2 \cdot a_3)$
Угол скоса:
$\theta = \cos^{-1} \left( -\frac{(a_1 \times a_3) \cdot (a_2 \times a_3)}{|a_1 \times a_3| \cdot |a_2 \times a_3|} \right)$
Масштабные коэффициенты:
$\alpha = \rho^2 |a_1 \times a_3| \sin \theta$
$\beta = \rho^2 |a_2 \times a_3| \sin \theta$
Формулы для вычисления внешних параметров (7)
Матрица вращения:
$r_1 = \frac{a_2 \times a_3}{|a_2 \times a_3|}$
$r_2 = r_3 \times r_1$
$r_3 = \rho a_3$
Вектор переноса:
$T = \rho K^{-1} b$
При подготовке данных для процедуры калибровки важно учитывать особые случаи, при которых процесс может дать некорректные результаты. Вырожденные конфигурации возникают, когда точки $P_i$ располагаются в одной плоскости или лежат на кривой пересечения двух квадрик. В таких случаях система уравнений становится неразрешимой, что приводит к невозможности корректного определения параметров камеры. Чтобы избежать подобных проблем, следует тщательно подходить к процессу калибровки. Необходимо использовать точки с различной глубиной расположения, обеспечивать разнообразие положений калибровочной мишени в пространстве и внимательно следить за распределением точек. Важно также проверять качество получаемых данных и анализировать корректность результатов на тестовых наборах. Для более глубокого понимания теоретических аспектов рекомендуется обратиться к разделу 1.3.1 учебника Forsyth & Ponce, где подробно рассматриваются вырожденные конфигурации и методы их предотвращения.
2. Компенсация искажений при калибровке камеры
До этого момента мы рассматривали идеальные линзы, свободные от любых искажений. Однако в реальности объективы могут отклоняться от прямолинейной проекции, что требует применения более сложных методов обработки. В этом разделе мы кратко рассмотрим подходы к работе с искажениями.
Благодаря физической симметрии линзы, радиальные искажения тоже обладают симметрией. Для моделирования радиальных искажений используется изотропное преобразование $Q$:
$Q P_i = \begin{bmatrix} q_1 \\ q_2 \\ q_3 \end{bmatrix} P_i = \begin{bmatrix} \frac{1}{\lambda} & 0 & 0 \\ 0 & \frac{1}{\lambda} & 0 \\ 0 & 0 & 1 \end{bmatrix} M P_i = \begin{bmatrix} u_i \\ v_i \end{bmatrix} = p_i$ (8)
Переписав в систему векторных уравнений, получаем:
$u_i q_3 P_i = q_1 P_i$
$v_i q_3 P_i = q_2 P_i$
Однако такая система перестаёт быть линейной, и для её решения требуются методы нелинейной оптимизации, которые подробно рассматриваются в разделе 22.2 учебника Forsyth & Ponce.
Упростить процесс нелинейной оптимизации при калибровке можно, сделав определённые допущения. В случае радиальных искажений важно отметить, что соотношение между координатами $u_i$ и $v_i$ остаётся неизменным. Это соотношение можно вычислить следующим образом:
$\frac{u_i}{v_i} = \frac{\frac{m_1P_i}{m_3P_i}}{\frac{m_2P_i}{m_3P_i}} = \frac{m_1P_i}{m_2P_i}$ (18)
При наличии $n$ соответствий мы можем составить систему линейных уравнений следующего вида:
$v_1(m_1P_1) - u_1(m_2P_1) = 0$
$\vdots$
$v_n(m_1P_n) - u_n(m_2P_n) = 0$
Эта система может быть представлена в виде матрично-векторного произведения, решаемого с помощью сингулярного разложения (SVD):
$L n = \begin{bmatrix} v_1P_1^T & -u_1P_1^T \\ \vdots & \vdots \\ v_nP_n^T & -u_nP_n^T \end{bmatrix} \begin{bmatrix} m_1^T \\ m_2^T \end{bmatrix}$ (19)
После оценки векторов $m_1$ и $m_2$ вектор $m_3$ может быть выражен как нелинейная функция от $m_1$, $m_2$ и $\lambda$. Это приводит к необходимости решения задачи нелинейной оптимизации, которая значительно проще исходной задачи оценки элементов матрицы $Q$.
Процесс решения включает следующие этапы:
- Формирование матрицы $L n$ на основе известных соответствий между точками
- Применение SVD для нахождения $m_1$ и $m_2$
- Вычисление $m_3$ через нелинейную зависимость
Используем условие ортогональности:
$m_1 \cdot m_3 = 0$
$m_2 \cdot m_3 = 0$
Учитываем нормировку:
$|m_3| = 1$
Вводим зависимость от параметра $\lambda$, итоговая формула для вычисления $m_3$ имеет вид:
$m_3 = \frac{m_1 \times m_2}{|m_1 \times m_2|} \cdot g(\lambda)$
где $g(\lambda)$ — некоторая функция от параметра $\lambda$, зависящая от конкретной модели искажений.
Вид функции $g(\lambda)$ зависит от требуемой точности модели.
Полиномиальная модель общего вида:
$g(\lambda) = 1 + k_1\lambda^2 + k_2\lambda^4 + k_3\lambda^6 + ...$
где $k_1, k_2, k_3$ — коэффициенты радиальных искажений.
На практике используют вычислительно несложные модели:
$g(\lambda) = 1 + k_1\lambda^2$
или
$g(\lambda) = 1 + k_1\lambda^2 + k_2\lambda^4$
Модель Брауна включает как радиальные, так и тангенциальные искажения:
$x_{distorted} = x(1 + k_1r^2 + k_2r^4) + 2p_1xy + p_2(r^2 + 2x^2)$
$y_{distorted} = y(1 + k_1r^2 + k_2r^4) + p_1(r^2 + 2y^2) + 2p_2xy$
где $r^2 = x^2 + y^2$
Резюме
Калибровка камеры — это комплексный процесс определения внутренних и внешних параметров оптической системы для точного преобразования координат между трёхмерным пространством и двумерным изображением. В основе калибровки лежит использование калибровочной мишени с известными координатами, что позволяет установить соответствие между мировыми и экранными координатами. Процесс включает определение матрицы камеры, которая содержит информацию о фокусном расстоянии, координатах главной точки и коэффициентах искажения.
Важным этапом является учёт искажений, которые неизбежно присутствуют в реальных объективах. Для их компенсации применяются специальные математические модели, чаще всего основанные на полиномиальных функциях радиальных искажений. При калибровке необходимо избегать вырожденных конфигураций, когда точки располагаются в одной плоскости, что делает невозможным корректное определение параметров. Практическая реализация требует достаточного количества калибровочных изображений с разнообразным расположением мишени относительно камеры. После завершения калибровки получается набор параметров, позволяющий компенсировать искажения и восстанавливать пространственные координаты по изображениям с точностью до удаления $z$.
Качество калибровки напрямую влияет на точность последующих измерений и является критически важным этапом в системах компьютерного зрения и машинного обучения.