Сверточные сети. Введение
Сверточные сети. Введение
Сожержание: - Краткое вступление без мозговых аналогий - Моделирование одного нейрона + Биологическая мотивация и связи + Одиночный нейрон как линейный классификатор + Часто используемые функции активации - Архитектуры нейронных сетей + Многоуровневая организация + Пример вычисления с прямой связью + Представительская власть + Настройка количества слоев и их размеров - Краткие сведения - Дополнительные ссылки
Краткое вступление
Можно представить нейронные сети, не прибегая к аналогам с мозгом. В разделе о линейной классификации мы вычисляли баллы для различных визуальных категорий по изображению с помощью формулы s=Wx, где W была матрицей и x был вектор входных данных, содержащий все пиксельные данные изображения. В случае CIFAR-10 x является вектором-столбцом [3072x1], и W. Это матрица [10x3072], так что выходные данные представляют собой вектор из 10 оценок по классам.
Примерная нейронная сеть вместо этого вычисляла бы \( s = \( W_2 \max(0, W_1 x) \). Здесь, \(W_1\) может быть, например, матрицей [100x3072], преобразующей изображение в 100-мерный промежуточный вектор. Функция \(max(0,-) \) это нелинейность, котрая применяется поэлементно. Существует несколько вариантов нелинейности (которые мы рассмотрим ниже), но этот вариант является распространённым и просто приравнивает все значения ниже нуля к нулю. Наконец, матрица \(W_2\) тогда будет иметь размер [10x100], так что мы снова получим 10 чисел, которые мы интерпретируем как оценки классов. Обратите внимание, что нелинейность имеет решающее значение с точки зрения вычислений — если бы мы её не использовали, то две матрицы можно было бы объединить в одну, и, следовательно, прогнозируемые оценки классов снова были бы линейной функцией входных данных. Нелинейность — это то, что даёт нам колебания. Параметры W2,W1. Они обучаются с помощью стохастического градиентного спуска, а их градиенты вычисляются с помощью правила дифференцирования (и обратного распространения ошибки).
Аналогично трехслойная нейронная сеть могла бы выглядеть следующим образом \( s = W_3 \max(0, W_2 \max(0, W_1 x)) \), где все \(W_3, W_2, W_1\)- это параметры, которые необходимо изучить. Размеры промежуточных скрытых векторов являются гиперпараметрами сети, и мы рассмотрим, как их можно задать позже. Теперь давайте посмотрим, как можно интерпретировать эти вычисления с точки зрения нейронов/сети.
Моделирование одного нейрона
Изначально область нейронных сетей была в первую очередь ориентирована на моделирование биологических нейронных систем, но с тех пор она расширилась и стала заниматься разработкой и достижением хороших результатов в задачах машинного обучения. Тем не менее, мы начнём наше обсуждение с очень краткого и общего описания биологической системы, которая послужила источником вдохновения для значительной части этой области.
Биологическая мотивация и связи
Основной вычислительной единицей мозга является нейрон. В нервной системе человека насчитывается около 86 миллиардов нейронов, и они соединены примерно с 10^14 — 10^15 синапсами. На схеме ниже показан схематичный рисунок биологического нейрона (сверху) и распространённая математическая модель (снизу). Каждый нейрон получает входные сигналы от своих дендритов и выдаёт выходные сигналы по своему (единственному) аксону. В конечном итоге аксон разветвляется и соединяется через синапсы с дендритами других нейронов. В вычислительной модели нейрона сигналы, которые проходят по аксонам (например, \(x_0\) взаимодействуют мультипликативно (например, \(w_0 x_0\) с дендритами другого нейрона в зависимости от силы синапса (например, \(w_0\). Идея заключается в том, что синаптические силы (веса w) являются обучаемыми и контролируют силу влияния (и его направление: возбуждающее (положительный вес) или тормозящее (отрицательный вес) одного нейрона на другой. В базовой модели дендриты передают сигнал в тело клетки, где он суммируется. Если итоговая сумма превышает определённый порог, нейрон может сработать, отправив импульс по своему аксону. В вычислительной модели мы предполагаем, что точное время срабатывания импульсов не имеет значения и что информация передаётся только частотой срабатывания. Основываясь на этой интерпретации, это частотного кода, мы моделируем частоту срабатывания нейрона с помощью функции активации f, которая представляет собой частоту импульсов вдоль аксона. Исторически сложилось так, что в качестве функции активации часто используется сигмоидальная функция σ, поскольку она принимает вещественные входные данные (силу сигнала после суммирования) и преобразует их в диапазон от 0 до 1. Подробнее об этих функциях активации мы поговорим далее в этом разделе.
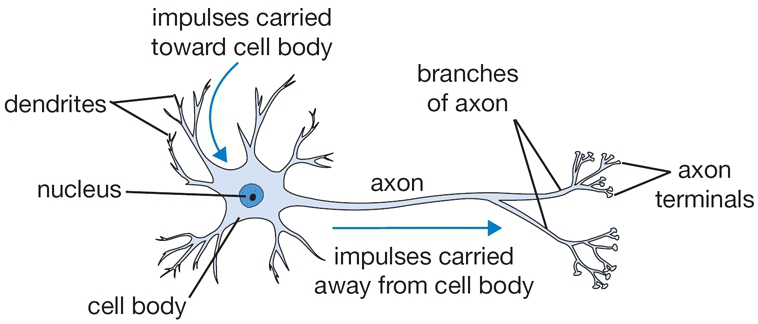
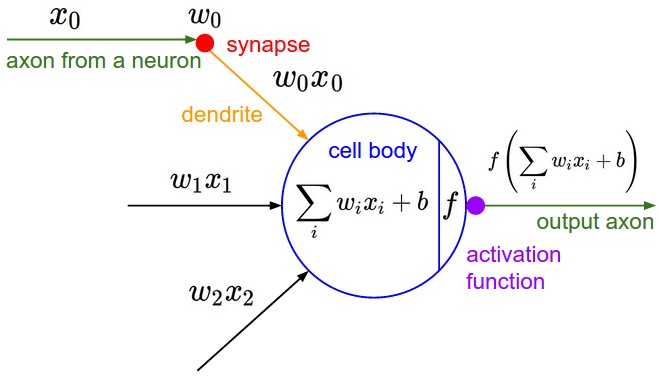
Карикатурное изображение биологического нейрона (сверху) и его математическая модель (снизу).
Пример кода для прямого распространения сигнала по одному нейрону может выглядеть следующим образом:
class Neuron(object): # ... def forward(self, inputs): """ assume inputs and weights are 1-D numpy arrays and bias is a number """ cell_body_sum = np.sum(inputs * self.weights) + self.bias firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function return firing_rate
Другими словами, каждый нейрон выполняет скалярное произведение входных данных и своих весов, добавляет смещение и применяет нелинейность (или функцию активации), в данном случае сигмоидальную ** sigmoid \(\sigma(x) = 1/(1+e^{-x})\)**. Более подробно о различных функциях активации мы расскажем в конце этого раздела.
Грубая модель. Важно подчеркнуть, что эта модель биологического нейрона является очень грубой: например, существует множество различных типов нейронов, каждый из которых обладает своими свойствами. Дендриты в биологических нейронах выполняют сложные нелинейные вычисления. Синапсы — это не просто один вес, это сложная нелинейная динамическая система. Известно, что точное время выходных импульсов во многих системах имеет большое значение, что позволяет предположить, что приближение кода скорости может не работать. Из-за всех этих и многих других упрощений будьте готовы к тому, что любой, кто разбирается в нейробиологии, будет возмущаться, если вы проведёте аналогию между нейронными сетями и реальным мозгом. Если вам интересно, ознакомьтесь с этим обзором (в формате pdf) или с этим обзором, опубликованным недавно.
Одиночный нейрон как линейный классификатор
Математическая форма прямого вычисления модели нейрона может показаться вам знакомой. Как мы видели на примере линейных классификаторов, нейрон может «любить» (активация близка к единице) или «не любить» (активация близка к нулю) определённые линейные области своего входного пространства. Следовательно, с помощью подходящей функции потерь на выходе нейрона мы можем превратить один нейрон в линейный классификатор:
Бинарный классификатор Softmax. Например, мы можем интерпретировать \(\sigma(\sum_i * w_i * x_i + b)\ ),как вероятность_ одного из классов \(P(y_i = 1 \mid x_i; w) \). Вероятность появления другого класса была бы равна \(P(y_i = 0 \mid x_i; w) = 1 - P(y_i = 1 \mid x_i; w) \), так как их сумма должна быть равна единице. С помощью этой интерпретации мы можем сформулировать функцию потерь перекрёстной энтропии, как мы видели в разделе «Линейная классификация», и оптимизация этой функции приведёт к созданию бинарного классификатора Softmax (также известного как логистическая регрессия). Поскольку сигмоидальная функция принимает значения от 0 до 1, прогнозы этого классификатора основаны на том, превышает ли выходное значение нейрона 0,5.
Бинарный классификатор SVM. В качестве альтернативы мы могли бы добавить к выходу нейрона функцию потерь с максимальным зазором и обучить его как бинарную машину опорных векторов.
Интерпретация регуляризации. В этом биологическом контексте потеря регуляризации в обоих случаях SVM/Softmax может быть интерпретирована как постепенное забывание, поскольку она приводит к уменьшению всех синаптических весов w приближается к нулю после каждого обновления параметра.
Один нейрон можно использовать для реализации бинарного классификатора (например, бинарного классификатора Softmax или бинарного классификатора SVM)
Часто используемые функции активации
Каждая функция активации (или нелинейность) принимает одно число и выполняет над ним определённую фиксированную математическую операцию. На практике вы можете столкнуться с несколькими функциями активации:
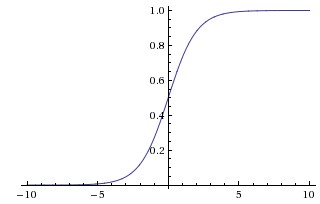
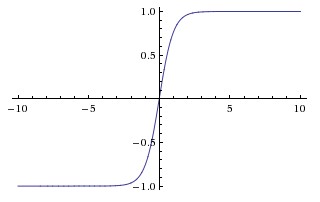
Сверху: сигмоидальная нелинейность сжимает действительные числа до диапазона [0,1].
Справа: нелинейность tanh сжимает действительные числа до диапазона [-1,1].
Сигмоида. Сигмоидальная нелинейность имеет математическую форму \(\sigma(x) = 1 / (1 + e^{-x})\). Она показана на изображении выше слева. Как упоминалось в предыдущем разделе, она принимает вещественное число и «сжимает» его до диапазона от 0 до 1. В частности, большие отрицательные числа становятся равными 0, а большие положительные числа становятся равными 1. Сигмоидальная функция часто использовалась в прошлом, так как её можно интерпретировать как частоту срабатывания нейрона: от полного отсутствия срабатывания (0) до полного срабатывания с предполагаемой максимальной частотой (1). На практике сигмоидальная нелинейность в последнее время вышла из моды и используется редко. У неё есть два основных недостатка:
- Сигмоиды насыщаются и уничтожают градиенты. Очень нежелательное свойство сигмоидального нейрона заключается в том, что, когда активация нейрона насыщается на одном из концов 0 или 1, градиент в этих областях почти равен нулю. Напомним, что во время обратного распространения ошибки этот (локальный) градиент будет умножен на градиент выхода этого нейрона для всей задачи. Поэтому, если локальный градиент очень мал, он фактически «уничтожит» градиент, и почти никакой сигнал не пройдёт через нейрон к его весам и рекурсивно к его данным. Кроме того, необходимо соблюдать особую осторожность при инициализации весов сигмоидальных нейронов, чтобы предотвратить перегрузку. Например, если начальные веса слишком велики, то большинство нейронов будут перегружены, и сеть едва ли будет обучаться.
- Сигмоидальные выходные данные не центрированы по нулю. Это нежелательно, так как нейроны на более поздних уровнях обработки в нейронной сети (подробнее об этом позже) будут получать данные, не центрированные по нулю. Это влияет на динамику во время градиентного спуска, потому что если данные, поступающие в нейрон, всегда положительные (например, x>0 поэлементно в \(f = w^Tx + b\))), тогда градиент по весам w во время обратного распространения ошибки все значения станут либо положительными, либо отрицательными (в зависимости от градиента всего выражения f). Это может привести к нежелательной зигзагообразной динамике в обновлении градиентов весовых коэффициентов. Однако обратите внимание, что после суммирования этих градиентов по пакету данных окончательное обновление весовых коэффициентов может иметь разные знаки, что несколько смягчает эту проблему. Таким образом, это неудобство, но его последствия менее серьёзны по сравнению с проблемой насыщенной активации, описанной выше.
Tanh. Нелинейность tanh показана на изображении выше снизу. Она сжимает вещественное число до диапазона [-1, 1]. Как и в случае с сигмоидальным нейроном, его активация насыщается, но, в отличие от сигмоидального нейрона, его выходная величина смещена относительно нуля. Поэтому на практике нелинейность tanh всегда предпочтительнее сигмоидальной нелинейности. Также обратите внимание, что нейрон tanh — это просто масштабированный сигмоидальный нейрон, из-за чего, в частности, верно следующее: \( \tanh(x) = 2 \sigma(2x) -1 \).
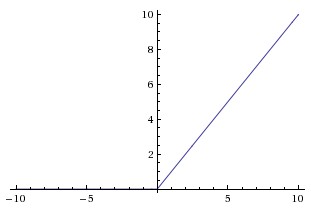
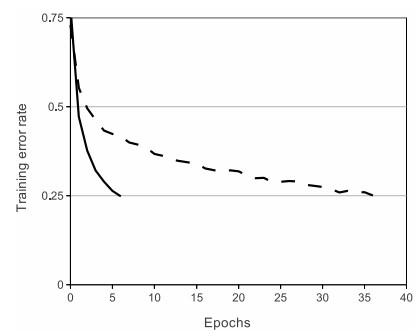
Сверху: функция активации выпрямленной линейной единицы (ReLU), которая равна нулю, когда x < 0, а затем линейна с наклоном 1, когда x > 0.
Снизу: график из статьи Крижевски и др. (pdf), показывающий 6-кратное улучшение сходимости с модулем ReLU по сравнению с модулем tanh.
ReLU. Выпрямленный линейный блок стал очень популярным в последние несколько лет. Он вычисляет функцию \(f(x) = \max(0, x)\). Другими словами, активация просто ограничивается нулём (см. изображение выше сверху). У использования ReLU есть несколько плюсов и минусов:
- (+) Было обнаружено, что она значительно ускоряет (например, в 6 раз в Крижевски и др.) сходимость стохастического градиентного спуска по сравнению с сигмоидальными/тангенциальными функциями. Утверждается, что это связано с её линейной, ненасыщаемой формой.
- (+) По сравнению с нейронами tanh/сигмоидными нейронами, которые требуют дорогостоящих операций (экспоненциальных и т. д.), ReLU можно реализовать, просто установив пороговое значение для матрицы активации равным нулю.
- (-) К сожалению, блоки ReLU могут быть нестабильными во время обучения и могут «умирать» . Например, большой градиент, проходящий через нейрон ReLU, может привести к обновлению весов таким образом, что нейрон больше никогда не активируется ни для одной точки данных. Если это произойдёт, то градиент, проходящий через блок, с этого момента будет равен нулю. То есть блоки ReLU могут необратимо «умирать» во время обучения, поскольку они могут быть отброшены от множества данных. Например, если скорость обучения установлена слишком высокой, вы можете обнаружить, что до 40% вашей сети могут быть «мёртвыми» (то есть нейроны, которые никогда не активируются на протяжении всего набора обучающих данных). При правильной настройке скорости обучения эта проблема возникает реже.
Протекающий ReLU. Протекающий ReLU — это одна из попыток решить проблему «умирающего ReLU». Вместо того чтобы быть равной нулю при x < 0, функция просачивающегося ReLU будет иметь небольшой положительный наклон (около 0,01). То есть функция вычисляет \(f(x) = \mathbb{1}(x < 0) (\alpha x) + \mathbb{1}(x>=0) (x) \) where \(\alpha\), где α- это небольшая константа. Некоторые люди сообщают об успехах с использованием этой формы функции активации, но результаты не всегда стабильны. Наклон в отрицательной области также может быть параметром каждого нейрона, как в случае с нейронами PReLU, представленными в работе «Глубокое погружение в выпрямители» Кайминга Хэ и др., 2015. Однако в настоящее время неясно, насколько стабильны преимущества при выполнении разных задач.
Maxout. Были предложены другие типы устройств, которые не имеют функциональной формы \(f(w^Tx + b)\), где нелинейность применяется к скалярному произведению весов и данных. Одним из относительно популярных вариантов является нейрон Maxout (введённый недавно Goodfellowи др.), который обобщает ReLU и его неидеальную версию. Нейрон Maxout вычисляет функцию \(\max(w_1^Tx+b_1, w_2^Tx + b_2)\). Обратите внимание, что и ReLU, и Leaky ReLU являются частным случаем этой формы (например, для ReLU мы имеем \(w_1, b_1 = 0\)). Таким образом, нейрон Maxout обладает всеми преимуществами блока ReLU (линейный режим работы, отсутствие насыщения) и не имеет его недостатков (умирающий ReLU). Однако, в отличие от нейронов ReLU, он удваивает количество параметров для каждого отдельного нейрона, что приводит к большому общему количеству параметров.
На этом мы завершаем обсуждение наиболее распространённых типов нейронов и их функций активации. В качестве последнего комментария: очень редко в одной сети сочетаются разные типы нейронов, хотя в этом нет принципиальных проблем.
TLDR: «Какой тип нейронов мне следует использовать?» Используйте нелинейность ReLU, будьте осторожны с темпами обучения и, возможно, отслеживайте долю «мёртвых» нейронов в сети. Если вас это беспокоит, попробуйте Leaky ReLU или Maxout. Никогда не используйте сигмоид. Попробуйте tanh, но будьте готовы к тому, что он будет работать хуже, чем ReLU/Maxout.
Архитектуры нейронных сетей
Многоуровневая организация
Нейронные сети как нейроны в графах. Нейронные сети моделируются как совокупности нейронов, соединённых в ациклический граф. Другими словами, выходные данные одних нейронов могут становиться входными данными для других нейронов. Циклы недопустимы, так как это привело бы к бесконечному циклу при прямом проходе сети. Вместо аморфных скоплений соединённых нейронов модели нейронных сетей часто состоят из отдельных слоёв нейронов. Для обычных нейронных сетей наиболее распространённым типом слоёв является слой с полной связью, в котором нейроны между двумя соседними слоями полностью соединены попарно, но нейроны в пределах одного слоя не имеют общих связей. Ниже приведены два примера топологий нейронных сетей, в которых используется набор слоёв с полной связью:
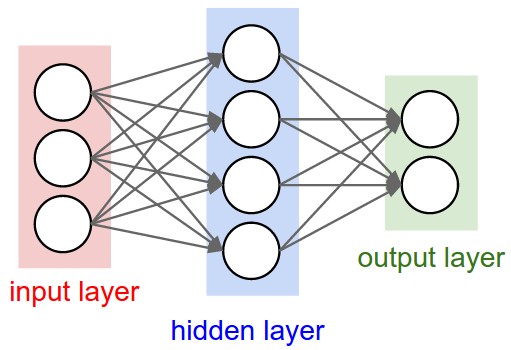
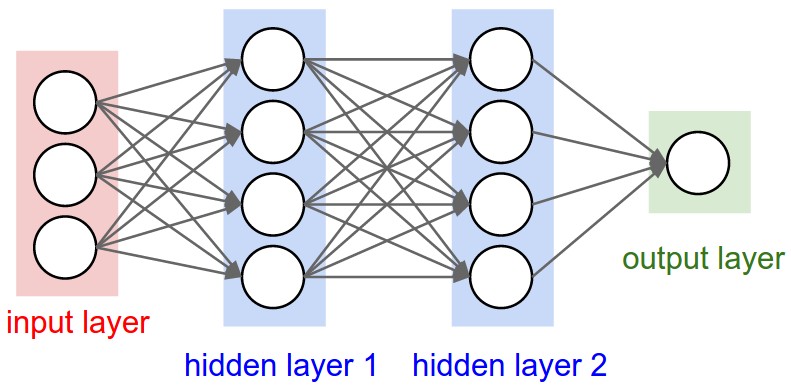
Сверху: двухслойная нейронная сеть (один скрытый слой из 4 нейронов (или единиц) и один выходной слой из 2 нейронов) с тремя входами. Снизу: трёхслойная нейронная сеть с тремя входами, двумя скрытыми слоями по 4 нейрона в каждом и одним выходным слоем. Обратите внимание, что в обоих случаях между нейронами разных слоёв есть связи (синапсы), но не внутри слоя.
Соглашения об именовании. Обратите внимание, что, когда мы говорим о N-слойной нейронной сети, мы не учитываем входной слой. Таким образом, однослойная нейронная сеть — это сеть без скрытых слоёв (входные данные напрямую преобразуются в выходные). В этом смысле иногда можно услышать, что логистическая регрессия или метод опорных векторов — это просто частный случай однослойных нейронных сетей. Вы также можете услышать, что эти сети называют «искусственными нейронными сетями» (ИНС) или «многослойными перцептронами» (МПП). Многим не нравятся аналогии между нейронными сетями и реальным мозгом, и они предпочитают называть нейроны единицами.
Выходной слой. В отличие от всех остальных слоёв нейронной сети, нейроны выходного слоя чаще всего не имеют функции активации (или можно считать, что у них линейная функция активации). Это связано с тем, что последний выходной слой обычно используется для представления оценок классов (например, при классификации), которые являются произвольными действительными числами, или для представления некоторой действительной цели (например, при регрессии).
Размер нейронных сетей. Два показателя, которые обычно используются для измерения размера нейронных сетей, — это количество нейронов или, чаще, количество параметров. Рассмотрим две сети на рисунке выше: - В первой сети (слева) 4 + 2 = 6 нейронов (не считая входных данных), (3 x 4) + (4 x 2) = 20 весовых коэффициентов и 4 + 2 = 6 смещений, всего 26 обучаемых параметров. - Во второй сети (справа) 4 + 4 + 1 = 9 нейронов, (3 x 4) + (4 x 4) + (4 x 1) = 12 + 16 + 4 = 32 весовых коэффициента и 4 + 4 + 1 = 9 смещений, всего 41 обучаемый параметр.
Для сравнения: современные свёрточные нейронные сети содержат порядка 100 миллионов параметров и обычно состоят примерно из 10–20 слоёв (отсюда глубокое обучение). Однако, как мы увидим, количество эффективных связей значительно больше из-за совместного использования параметров. Подробнее об этом в модуле «Свёрточные нейронные сети».
Пример вычисления с прямой связью
Повторное матричное умножение в сочетании с функцией активации. Одна из основных причин, по которой нейронные сети организованы в виде слоёв, заключается в том, что такая структура позволяет очень просто и эффективно оценивать нейронные сети с помощью матричных векторных операций. Если рассматривать трёхслойную нейронную сеть на приведённой выше схеме, то входными данными будет вектор [3x1]. Все весовые коэффициенты для слоя можно хранить в одной матрице. Например, веса первого скрытого слоя W1 будут иметь размер [4x3], а смещения для всех нейронов будут находиться в векторе b1 размером [4x1]. Здесь каждый нейрон имеет свои веса в строке W1, поэтому умножение матрицы на вектор np.dot(W1,x) вычисляет активации всех нейронов в этом слое. Аналогично, W2 будет матрицей [4x4], которая хранит связи второго скрытого слоя, а W3 — матрицей [1x4] для последнего (выходного) слоя. Полный прямой проход этой трёхслойной нейронной сети — это просто три матричных умножения, объединённых с применением функции активации:
# forward-pass of a 3-layer neural network: f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid) x = np.random.randn(3, 1) # random input vector of three numbers (3x1) h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1) h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1) out = np.dot(W3, h2) + b3 # output neuron (1x1)
В приведённом выше коде W1,W2,W3,b1,b2,b3 — это обучаемые параметры сети. Обратите внимание, что вместо одного входного вектора-столбца переменная x может содержать целую выборку обучающих данных (где каждый входной пример будет столбцом x), и тогда все примеры будут эффективно обрабатываться параллельно. Обратите внимание, что последний слой нейронной сети обычно не имеет функции активации (например, он представляет собой (числовое) значение класса в задаче классификации).
Прямой проход полносвязного слоя соответствует одному умножению матриц, за которым следует смещение и функция активации.
Представительская власть
Один из способов взглянуть на нейронные сети с полносвязными слоями заключается в том, что они определяют семейство функций, параметры которых задаются весовыми коэффициентами сети. Возникает естественный вопрос: какова репрезентативная мощность этого семейства функций? В частности, существуют ли функции, которые нельзя смоделировать с помощью нейронной сети?
Оказывается, что нейронные сети, содержащие хотя бы один скрытый слой, являются универсальными аппроксиматорами. То есть можно показать (например, см. «Аппроксимацию суперпозициями сигмоидальных функций» 1989 года (pdf) или это интуитивное объяснение Майкла Нильсена), что для любой непрерывной функции f(x) и некоторые ϵ>0, существует Нейронная сеть g(x)_ с одним скрытым слоем (с разумным выбором нелинейности, например, сигмоидальной) таким образом, что ∀x,∣f(x)−g(x)∣<ϵ__. Другими словами, нейронная сеть может аппроксимировать любую непрерывную функцию.
Если для аппроксимации любой функции достаточно одного скрытого слоя, зачем использовать больше слоёв и углубляться в детали? Ответ заключается в том, что тот факт, что двухслойная нейронная сеть является универсальным аппроксиматором, хоть и выглядит красиво с математической точки зрения, на практике является относительно слабым и бесполезным утверждением. В одномерном пространстве функция «сумма пиков индикаторов» \(g(x) = \sum_i c_i \mathbb{1}(a_i < x < b_i)\), где \(a,b,c\). Векторы параметров также являются универсальным аппроксиматором, но никто не предлагает использовать эту функциональную форму в машинном обучении. Нейронные сети хорошо работают на практике, потому что они компактно выражают красивые, плавные функции, которые хорошо согласуются со статистическими свойствами данных, с которыми мы сталкиваемся на практике, а также легко обучаются с помощью наших алгоритмов оптимизации (например, градиентного спуска). Точно так же тот факт, что более глубокие сети (с несколькими скрытыми слоями) могут работать лучше, чем сети с одним скрытым слоем, является эмпирическим наблюдением, несмотря на то, что их репрезентативная мощность одинакова.
Кстати, на практике часто бывает так, что 3-слойные нейронные сети превосходят 2-слойные, но ещё большее количество слоёв (4, 5, 6) редко приносит большую пользу. Это резко контрастирует с свёрточными сетями, где глубина оказалась чрезвычайно важным компонентом для хорошей системы распознавания (например, порядка 10 обучаемых слоёв). Один из аргументов в пользу этого наблюдения заключается в том, что изображения имеют иерархическую структуру (например, лица состоят из глаз, которые состоят из контуров и т. д.), поэтому несколько уровней обработки интуитивно понятны для этой области данных.
Полная история, конечно, гораздо сложнее и является предметом многочисленных недавних исследований. Если вас интересуют эти темы, мы рекомендуем вам прочитать: - Книга «Глубокое обучение» Бенджио, Гудфеллоу, Курвиля, в частности глава 6.4. - Действительно ли Глубокие сети должны быть глубокими? - ФитНеты: Советы для тонких глубоких Сеток
Настройка количества слоев и их размеров
Как мы решаем, какую архитектуру использовать, когда сталкиваемся с практической задачей? Следует ли нам использовать несколько скрытых слоёв? Один скрытый слой? Два скрытых слоя? Насколько большим должен быть каждый слой? Во-первых, обратите внимание, что по мере увеличения размера и количества слоёв в нейронной сети ёмкость сети увеличивается. То есть пространство представимых функций растёт, поскольку нейроны могут взаимодействовать для выражения множества различных функций. Например, предположим, что у нас есть задача бинарной классификации в двух измерениях. Мы могли бы обучить три отдельные нейронные сети, каждая из которых имеет один скрытый слой определённого размера, и получить следующие классификаторы:
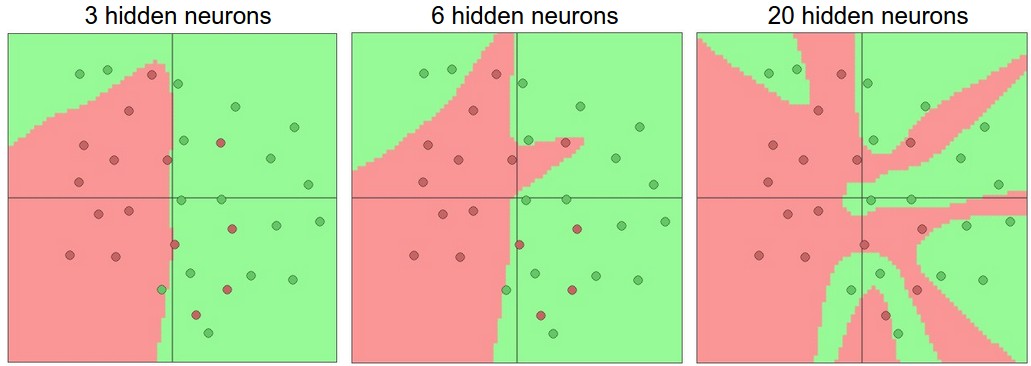
Более крупные нейронные сети могут представлять более сложные функции. Данные показаны в виде кружков, окрашенных в соответствии с их классом, а под ними показаны области принятия решений обученной нейронной сетью. Вы можете поиграть с этими примерами в этой демо-версии ConvNetsJS.
На приведённой выше схеме мы видим, что нейронные сети с большим количеством нейронов могут выполнять более сложные функции. Однако это одновременно и благо (поскольку мы можем научиться классифицировать более сложные данные), и проклятие (поскольку легче переобучиться на обучающих данных). Переобучение происходит, когда модель с высокой способностью к обучению подстраивается под шум в данных, а не под (предполагаемую) основную закономерность. Например, модель с 20 скрытыми нейронами подстраивается под все обучающие данные, но за счёт разделения пространства на множество непересекающихся красных и зелёных областей принятия решений. Модель с 3 скрытыми нейронами способна классифицировать данные только в общих чертах. Она моделирует данные как два сгустка и интерпретирует несколько красных точек внутри зелёного кластера как выбросы (шум). На практике это может привести к лучшему обобщению на тестовом наборе данных.
Исходя из нашего обсуждения выше, можно сделать вывод, что нейронные сети меньшего размера предпочтительнее, если данные недостаточно сложны, чтобы предотвратить переобучение. Однако это неверно — существует множество других предпочтительных способов предотвращения переобучения в нейронных сетях, которые мы обсудим позже (например, регуляризация \(L_2\), отсев, входной шум). На практике всегда лучше использовать эти методы для контроля переобучения, а не количество нейронов.
Тонкая причина этого заключается в том, что небольшие сети сложнее обучать с помощью локальных методов, таких как градиентный спуск: очевидно, что у их функций потерь относительно мало локальных минимумов, но оказывается, что многие из этих минимумов легче достигаются и являются плохими (то есть с высокими потерями). И наоборот, более крупные нейронные сети содержат значительно больше локальных минимумов, но эти минимумы оказываются гораздо лучше с точки зрения фактических потерь. Поскольку нейронные сети являются невыпуклыми, их свойства трудно изучать математически, но были предприняты некоторые попытки понять эти целевые функции, например, в недавней статье «Поверхности потерь в многослойных сетях». На практике вы обнаружите, что если вы обучаете небольшую сеть, то конечные потери могут сильно варьироваться — в некоторых случаях вам везёт, и вы сходитесь к хорошему результату, но в некоторых случаях вы застреваете в одном из плохих минимумов. С другой стороны, если вы обучите большую сеть, вы начнёте находить множество различных решений, но разброс в итоговых потерях будет намного меньше. Другими словами, все решения примерно одинаково хороши и в меньшей степени зависят от случайной инициализации.
Повторюсь, сила регуляризации — предпочтительный способ контроля переобучения нейронной сети. Мы можем рассмотреть результаты, полученные при трёх различных настройках:
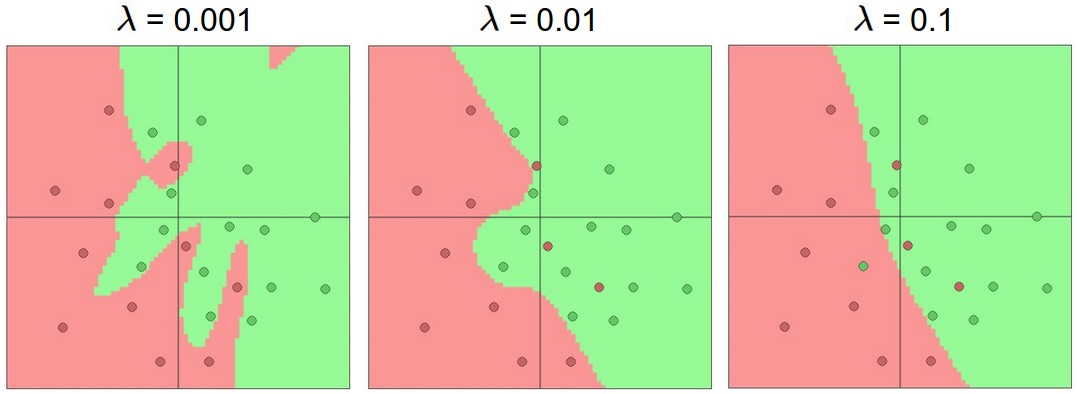
Влияние силы регуляризации: каждая из приведённых выше нейронных сетей имеет 20 скрытых нейронов, но изменение силы регуляризации делает области окончательного принятия решений более плавными при более высокой регуляризации. Вы можете поиграть с этими примерами в демонстрационной версии ConvNetsJS.
Вывод заключается в том, что вам не следует использовать более мелкие сети, потому что вы боитесь переобучения. Вместо этого вам следует использовать настолько большую нейронную сеть, насколько позволяет ваш вычислительный бюджет, и применять другие методы регуляризации для контроля переобучения.
Краткие сведения
Подводя итог: - Мы представили очень грубую модель биологического нейрона. - Мы рассмотрели несколько типов функций активации, которые используются на практике, и наиболее распространённым из них является ReLU. - Мы представили нейронные сети, в которых нейроны соединены полностью связанными слоями, где нейроны в соседних слоях имеют полные парные связи, но нейроны внутри слоя не соединены. - Мы увидели, что эта многоуровневая архитектура позволяет очень эффективно оценивать нейронные сети на основе матричных умножений, объединённых с применением функции активации. - Мы увидели, что нейронные сети являются универсальными аппроксиматорами функций, но мы также обсудили тот факт, что это свойство мало связано с их повсеместным использованием. Они используются потому, что делают определённые «правильные» предположения о функциональных формах функций, которые встречаются на практике. - Мы обсудили тот факт, что более крупные сети всегда будут работать лучше, чем сети меньшего размера, но их более высокая пропускная способность должна соответствующим образом регулироваться с помощью более сильной регуляризации (например, более высокого затухания весов), иначе они могут переобучаться. В следующих разделах мы рассмотрим другие формы регуляризации (особенно отсев).
Дополнительные ссылки
- deeplearning.net учебное пособие с Theano
- ConvNetJS демонстрации для интуиции
- Учебные пособия Майкла Нильсена