Предобработка, инициализация весов, функции потерь
Предобработка, инициализация весов, функции потерь
Содержание: - Настройка данных и модели + Предварительная обработка данных + Инициализация веса + Нормализация партии + Регуляризация (L2/L1/Maxnorm/Dropout) - Функции потерь - Краткая сводка
Настройка данных и модели
В предыдущем разделе мы представили модель нейрона, который вычисляет скалярное произведение с помощью нелинейности, и нейронные сети, которые объединяют нейроны в слои. Вместе эти решения определяют новую форму функции оценки, которую мы расширили по сравнению с простым линейным отображением, которое мы рассматривали в разделе «Линейная классификация». В частности, нейронная сеть выполняет последовательность линейных отображений с вложенными нелинейностями. В этом разделе мы обсудим дополнительные решения, касающиеся предварительной обработки данных, инициализации весов и функций потерь.
Предварительная обработка данных
Существует три распространённые формы предварительной обработки данных в матрице данных X, где мы будем предполагать, что X имеет размер [N x D] (N — количество данных, D — их размерность).
Вычитание среднего значения — наиболее распространённая форма предварительной обработки. Она заключается в вычитании среднего значения для каждого отдельного признака в данных и имеет геометрическую интерпретацию центрирования облака данных вокруг начала координат по каждому измерению. В numpy эта операция будет реализована следующим образом: (X -= np.mean(X, axis = 0). В случае с изображениями для удобства можно вычесть одно значение из всех пикселей (например, X -= np.mean(X)), либо сделать это отдельно для трёх цветовых каналов.
Нормализация — это приведение размерностей данных к примерно одинаковому масштабу. Существует два распространённых способа достижения такой нормализации:
- Один из них — разделить каждую размерность на её стандартное отклонение после центрирования по нулю: (X /= np.std(X, axis = 0)).
- Другой способ предварительной обработки — нормализовать каждую размерность так, чтобы минимальное и максимальное значения по каждой размерности составляли -1 и 1 соответственно. Имеет смысл применять эту предварительную обработку только в том случае, если у вас есть основания полагать, что разные входные параметры имеют разные масштабы (или единицы измерения), но они должны быть примерно одинаково важны для алгоритма обучения. В случае изображений относительные масштабы пикселей уже примерно одинаковы (и находятся в диапазоне от 0 до 255), поэтому нет необходимости выполнять этот дополнительный этап предварительной обработки.
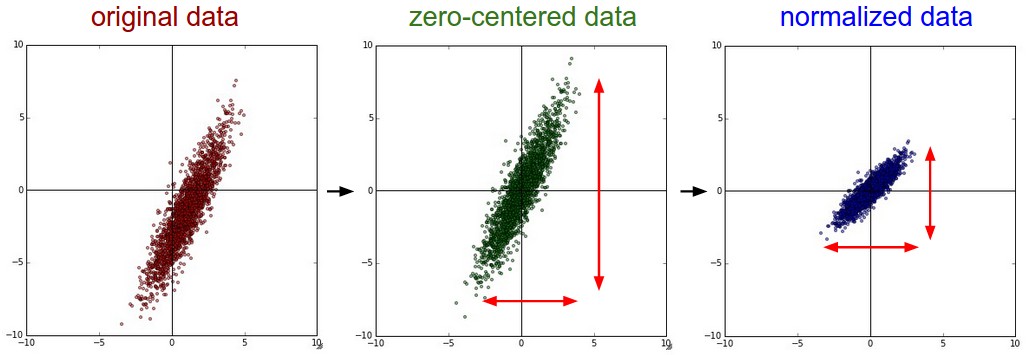
Общий конвейер предварительной обработки данных. Слева: исходные данные, 2-мерные входные данные. В центре: данные центрируются по нулевому значению путём вычитания среднего значения в каждом измерении. Облако данных теперь центрировано относительно начала координат. Справа: каждое измерение дополнительно масштабируется с помощью стандартного отклонения. Красные линии указывают на границы данных — в центре они разной длины, а справа — одинаковой.
Метод главных компонент и отбеливание — это ещё одна форма предварительной обработки. В этом процессе данные сначала центрируются, как описано выше. Затем мы можем вычислить ковариационную матрицу, которая показывает корреляционную структуру данных:
# Assume input data matrix X of size [N x D] X -= np.mean(X, axis = 0) # zero-center the data (important) cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix
Элемент (i,j) ковариационной матрицы данных содержит ковариацию между i-м и j-м измерениями данных. В частности, диагональ этой матрицы содержит дисперсии. Кроме того, ковариационная матрица является симметричной и положительно определённой. Мы можем вычислить разложение ковариационной матрицы данных по методу сингулярного разложения:
U,S,V = np.linalg.svd(cov)
где столбцы U являются собственными векторами, а S — одномерным массивом сингулярных значений. Чтобы устранить корреляцию в данных, мы проецируем исходные (но центрированные по нулю) данные на собственный базис:
Xrot = np.dot(X, U) # decorrelate the data
Обратите внимание, что столбцы U представляют собой набор ортогональных векторов (норма которых равна 1 и которые ортогональны друг другу), поэтому их можно рассматривать как базисные векторы. Таким образом, проекция соответствует повороту данных в X таким образом, чтобы новые оси были собственными векторами. Если бы мы вычислили ковариационную матрицу Xrot, то увидели бы, что теперь она диагональная. Преимущество np.linalg.svd в том, что в возвращаемом значении U столбцы собственных векторов отсортированы по собственным значениям. Мы можем использовать это для уменьшения размерности данных, используя только несколько главных собственных векторов и отбрасывая измерения, в которых данные не имеют дисперсии. Это также иногда называют анализом главных компонент (PCA) для уменьшения размерности:
Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]
После этой операции мы уменьшили исходный набор данных размером [N x D] до размера [N x 100], сохранив 100 измерений данных, которые содержат наибольшую дисперсию. Очень часто можно добиться очень хорошей производительности, обучая линейные классификаторы или нейронные сети на наборах данных, уменьшенных с помощью метода главных компонент, что позволяет сэкономить место и время.
Последнее преобразование, которое вы можете увидеть на практике, — это отбеливание. Операция отбеливания преобразует данные в собственный базис и делит каждое измерение на собственное значение, чтобы нормализовать масштаб. Геометрическая интерпретация этого преобразования заключается в том, что если исходные данные представляют собой многомерную гауссову функцию, то отбелённые данные будут представлять собой гауссову функцию с нулевым средним значением и единичной ковариационной матрицей. Этот шаг будет выглядеть следующим образом:
# whiten the data: # divide by the eigenvalues (which are square roots of the singular values) Xwhite = Xrot / np.sqrt(S + 1e-5)
Предупреждение: усиливается шум. Обратите внимание, что мы добавляем 1e-5 (или небольшую константу), чтобы предотвратить деление на ноль. Одним из недостатков этого преобразования является то, что оно может сильно усиливать шум в данных, поскольку растягивает все измерения (включая несущественные измерения с небольшой дисперсией, которые в основном являются шумом) до одинакового размера на входе. На практике это можно смягчить более сильным сглаживанием (т. е. увеличив 1e-5 до большего числа).
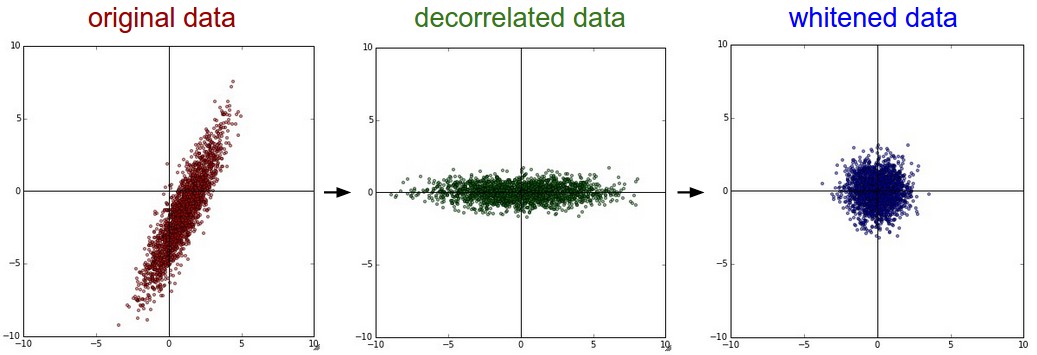
PCA / Отбеливание. Слева: оригинальная игрушка, 2-мерные входные данные. Посередине: после выполнения PCA. Данные центрируются на нуле, а затем поворачиваются в собственный базис ковариационной матрицы данных. Это декоррелирует данные (ковариационная матрица становится диагональной). Справа: каждое измерение дополнительно масштабируется по собственным значениям, преобразуя матрицу ковариации данных в единичную матрицу. Геометрически это соответствует растяжению и сжатию данных в изотропный гауссовский большой объект.
Мы также можем попытаться визуализировать эти преобразования с помощью изображений CIFAR-10. Обучающий набор CIFAR-10 имеет размер 50 000 x 3072, где каждое изображение растягивается в вектор-строку размером 3072. Затем мы можем вычислить ковариационную матрицу [3072 x 3072] и вычислить её разложение по методу сингулярного значения (что может быть относительно затратным). Как выглядят вычисленные собственные векторы визуально? Возможно, вам поможет изображение:

Слева: пример набора из 49 изображений. 2-е слева: 144 главных собственных вектора из 3072. Главные собственные векторы объясняют большую часть дисперсии данных, и мы видим, что они соответствуют более низким частотам на изображениях. 2-е справа: 49 изображений, уменьшенных с помощью метода главных компонент с использованием 144 показанных здесь собственных векторов. То есть вместо того, чтобы представлять каждое изображение в виде 3072-мерного вектора, где каждый элемент — это яркость конкретного пикселя в определённом месте и на определённом канале, каждое изображение выше представлено только 144-мерным вектором, где каждый элемент показывает, какая часть каждого собственного вектора составляет изображение. Чтобы увидеть, какая информация об изображении содержится в этих 144 числах, мы должны вернуться к «пиксельному» базису из 3072 чисел. Поскольку U — это поворот, этого можно добиться, умножив на U.transpose()[:144,:], а затем, визуализировав полученные 3072 числа в виде изображения, вы можете заметить, что изображения немного размыты, что отражает тот факт, что верхние собственные векторы захватывают более низкие частоты. Однако большая часть информации всё равно сохраняется. Справа: визуализация «белого» представления, в котором дисперсия по каждому из 144 измерений сжата до одинаковой длины. Здесь 144 «белых» числа возвращаются к пикселям изображения путём умножения на U.transpose()[:144,:]. Более низкие частоты (на которые изначально приходилось больше всего дисперсии) теперь незначительны, а более высокие частоты (на которые изначально приходилось относительно мало дисперсии) становятся более выраженными.
На практике. Мы упоминаем метод главных компонент/отбеливание в этих заметках для полноты картины, но эти преобразования не используются в свёрточных сетях. Однако очень важно центрировать данные по нулевому значению, и часто также выполняется нормализация каждого пикселя.
Распространённая ошибка. Важно отметить, что любая статистика предварительной обработки (например, среднее значение данных) должна рассчитываться только на обучающих данных, а затем применяться к проверочным/тестовым данным. Например, вычисление среднего значения и вычитание его из каждого изображения во всём наборе данных, а затем разделение данных на обучающие/проверочные/тестовые, было бы ошибкой. Вместо этого среднее значение должно рассчитываться только на обучающих данных, а затем вычитаться из всех разделов (обучающих/проверочных/тестовых).
Инициализация веса
Мы рассмотрели, как построить архитектуру нейронной сети и как предварительно обработать данные. Прежде чем приступить к обучению сети, необходимо инициализировать её параметры.
Ловушка: инициализация всех весов нулями. Давайте начнём с того, чего делать не следует. Обратите внимание, что мы не знаем, каким должно быть конечное значение каждого веса в обученной сети, но при правильной нормализации данных разумно предположить, что примерно половина весов будет положительной, а половина — отрицательной. Тогда разумной идеей может быть установка всех начальных весов в нулевое значение, что, как мы ожидаем, будет «наилучшим предположением». Это оказалось ошибкой, потому что если каждый нейрон в сети вычисляет один и тот же результат, значит все они также будут вычислять одни и те же градиенты во время обратного распространения ошибки и подвергаться одним и тем же обновлениям параметров. Другими словами, если веса нейронов инициализированы одинаково, то между ними не будет асимметрии.
Небольшие случайные числа. Поэтому мы по-прежнему хотим, чтобы весовые коэффициенты были очень близки к нулю, но, как мы уже говорили выше, не равнялись нулю. В качестве решения принято инициализировать весовые коэффициенты нейронов небольшими числами и называть это нарушением симметрии. Идея заключается в том, что изначально все нейроны случайны и уникальны, поэтому они будут вычислять разные обновления и интегрироваться в сеть как её различные части. Реализация для одной весовой матрицы может выглядеть так: W = 0.01* np.random.randn(D,H), где randn — выборки из гауссианы с нулевым средним и единичным стандартным отклонением. При такой формулировке вектор весов каждого нейрона инициализируется как случайный вектор, выбранный из многомерной гауссианы, поэтому нейроны ориентированы в случайном направлении во входном пространстве. Также можно использовать небольшие числа, выбранные из равномерного распределения, но на практике это, по-видимому, относительно мало влияет на конечную производительность.
Предупреждение: не обязательно, что меньшие числа будут работать лучше. Например, слой нейронной сети с очень маленькими весами во время обратного распространения ошибки будет вычислять очень маленькие градиенты для своих данных (поскольку этот градиент пропорционален значению весов). Это может значительно уменьшить «сигнал градиента», проходящий через сеть в обратном направлении, и стать проблемой для глубоких сетей.
Калибровка дисперсии с помощью 1/sqrt(n). Одна из проблем, связанных с вышеописанным предложением, заключается в том, что дисперсия выходных данных случайно инициализированного нейрона растёт с увеличением количества входных данных. Оказывается, мы можем нормализовать дисперсию выходных данных каждого нейрона до 1, масштабируя его вектор весов на квадратный корень из количества входов (т. е. количества входных данных). То есть рекомендуемая эвристика заключается в инициализации вектора весов каждого нейрона следующим образом: w = np.random.randn(n) / sqrt(n), где n — количество входных данных. Это гарантирует, что все нейроны в сети изначально имеют примерно одинаковое распределение выходных данных, и эмпирически улучшает скорость сходимости.
Схема вывода выглядит следующим образом:Рассмотрим внутренний продукт \(s = \sum_i^n w_i x_i\) между весами w и входные данные x, что даёт исходную активацию нейрона до нелинейности. Мы можем изучить дисперсию s:
$$ \begin{align} \text{Var}(s) &= \text{Var}(\sum_i^n w_ix_i) \\ &= \sum_i^n \text{Var}(w_ix_i) \\ &= \sum_i^n [E(w_i)]^2\text{Var}(x_i) + [E(x_i)]^2\text{Var}(w_i) + \text{Var}(x_i)\text{Var}(w_i) \\ &= \sum_i^n \text{Var}(x_i)\text{Var}(w_i) \\ &= \left( n \text{Var}(w) \right) \text{Var}(x) \end{align} $$
где на первых двух этапах мы использовали свойства дисперсии . На третьем этапе мы предположили, что входные данные и веса имеют нулевое среднее значение, поэтому \(E[x_i] = E[w_i] = 0\). Обратите внимание, что в общем случае это не так: например, блоки ReLU будут иметь положительное среднее значение. На последнем этапе мы предположили, что все \(w_i, x_i\) являются одинаково распределёнными. Из этого вывода следует, что если мы хотим s иметь ту же дисперсию, что и все его входные данные x, тогда во время инициализации мы должны убедиться, что дисперсия каждого веса w является 1/n. Следовательно при учете \(\text{Var}(aX) = a^2\text{Var}(X)\)) для случайной величины X и скаляра a говорит о необходимости взять единичный гауссовское распределение, а затем масштабировать его \(a = \sqrt{1/n}\), чтобы внести свой вклад в его дисперсию 1/n. Это дает инициализацию w = np.random.randn(n) / sqrt(n).
Аналогичный анализ проводится в статье «Понимание сложности обучения глубоких нейронных сетей прямого распространения» Глоро и др. В этой статье авторы в итоге рекомендуют инициализацию в виде Var(w)=2/(nin+nout), где \(n_in\), \(n_out)\ - это количество единиц в предыдущем слое и в следующем слое. Это основано на компромиссе и эквивалентном анализе градиентов обратного распространения. В более поздней статье на эту тему «Глубокое изучение выпрямителей: превосходные результаты на уровне человека при классификации ImageNet» Хе и др. выводится инициализация специально для нейронов ReLU, и делается вывод, что дисперсия нейронов в сети должна быть 2.0/n. Это даёт инициализацию w = np.random.randn(n) * sqrt(2.0/n) и является текущей рекомендацией для использования на практике в конкретном случае нейронных сетей с нейронами ReLU.
Разреженная инициализация. Другой способ решить проблему некалиброванных дисперсий — установить все весовые матрицы в нулевое значение, но для нарушения симметрии каждый нейрон случайным образом соединяется (с весами, выбранными из небольшого гауссовского распределения, как описано выше) с фиксированным количеством нейронов под ним. Типичное количество нейронов, с которыми можно соединиться, может составлять всего 10.
Инициализация смещений. Можно и часто бывает нужно инициализировать смещения равными нулю, поскольку асимметрия устраняется с помощью небольших случайных чисел в весовых коэффициентах. Для нелинейностей ReLU некоторые предпочитают использовать небольшое постоянное значение, например 0,01, для всех смещений, потому что это гарантирует, что все блоки ReLU срабатывают в начале и, следовательно, получают и передают некоторый градиент. Однако неясно, обеспечивает ли это стабильное улучшение (на самом деле некоторые результаты указывают на то, что это ухудшает производительность), и чаще всего используется просто инициализация с нулевым смещением.
На практике в настоящее время рекомендуется использовать блоки ReLU и w = np.random.randn(n) * sqrt(2.0/n) в соответствии с Хе и др..
Нормализация партии
Нормализация с помощью пакетов. Недавно разработанная Иоффе и Сегеди техника под названием «Нормализация с помощью пакетов» избавляет от многих проблем, связанных с правильной инициализацией нейронных сетей, поскольку в начале обучения активации во всей сети принудительно распределяются по единичному гауссовскому распределению. Основное наблюдение заключается в том, что это возможно, потому что нормализация — это простая дифференцируемая операция. При реализации этой техники обычно вставляется слой BatchNorm сразу после полносвязных слоёв (или свёрточных слоёв, как мы вскоре увидим) и перед нелинейностями. Мы не будем подробно останавливаться на этом методе, поскольку он хорошо описан в статье по ссылке, но отметим, что использование пакетной нормализации в нейронных сетях стало очень распространённой практикой. На практике сети, использующие пакетную нормализацию, значительно более устойчивы к неправильной инициализации. Кроме того, пакетную нормализацию можно интерпретировать как предварительную обработку на каждом слое сети, но интегрированную в саму сеть дифференцируемым образом. Здорово!
Регуляризация
Существует несколько способов контроля возможностей нейронных сетей для предотвращения переобучения:
Регуляризация L2 — это, пожалуй, самая распространённая форма регуляризации. Её можно реализовать, штрафуя за квадраты значений всех параметров непосредственно в целевой функции. То есть для каждого веса w в сети мы добавляем термин \(\frac{1}{2} \lambda w^2\) к цели, где λ является силой регуляризации. Обычно наблюдается фактор \(\frac{1}{2}\) впереди, потому что тогда градиент этого члена по отношению к параметру w это просто λw вместо 2λw.Регуляризация \(L_2\) интуитивно понятна: она сильно штрафует векторы с пиковыми значениями и отдаёт предпочтение векторам с размытыми значениями. Как мы обсуждали в разделе «Линейная классификация», из-за мультипликативных взаимодействий между весами и входными данными это позволяет сети использовать все входные данные понемногу, а не некоторые из них — по максимуму. Наконец, обратите внимание, что при обновлении параметров методом градиентного спуска использование регуляризации \(L_2\) в конечном итоге означает, что каждый вес уменьшается линейно: W += -lambda * W по направлению к нулю.
Регуляризация L1 — ещё одна относительно распространённая форма регуляризации, при которой для каждого веса w мы добавляем термин λ∣w∣ к цели. Можно комбинировать регуляризацию \(L_1\) с регуляризацией \(L_2\): \(\lambda_1 \mid w \mid + \lambda_2 w^2\) (это называется регуляризацией эластичной сети). Регуляризация \(L_1\) обладает интригующим свойством: она приводит к тому, что весовые векторы во время оптимизации становятся разреженными (то есть очень близкими к нулю). Другими словами, нейроны с регуляризацией \(L_1\) в конечном итоге используют только разреженное подмножество наиболее важных входных данных и становятся почти невосприимчивыми к «зашумлённым» входным данным. Для сравнения, конечные весовые векторы при регуляризации \(L_2\) обычно представляют собой размытые, небольшие числа. На практике, если вас не интересует явный выбор признаков, можно ожидать, что регуляризация \(L_2\) будет работать лучше, чем регуляризация \(L_1\).
Ограничения по максимальной норме. Другой формой регуляризации является установление абсолютной верхней границы для величины вектора весов каждого нейрона и использование проецируемого градиентного спуска для обеспечения соблюдения ограничения. На практике это соответствует обычному обновлению параметров, а затем обеспечению соблюдения ограничения путём ограничения вектора весов \(\vec{w}\) каждого нейрона, чтобы удовлетворить \(\Vert \vec{w} \Vert_2 < c\). Типичные значения c. Они составляют порядка 3 или 4. Некоторые пользователи сообщают об улучшениях при использовании этой формы регуляризации. Одно из её привлекательных свойств заключается в том, что сеть не может «взрывообразно» расти, даже если скорость обучения установлена слишком высокой, потому что обновления всегда ограничены.
Выпадение — чрезвычайно эффективный, простой и недавно представленный метод регуляризации, описанный Шриваставой и др. в «Выпадении: простом способе предотвращения переобучения нейронных сетей» (pdf), который дополняет другие методы (\(L_1\), \(L_2\), maxnorm). Во время обучения выпадение реализуется путём активации нейрона только с некоторой вероятностью p (гиперпараметр), или в противном случае установив его равным нулю.
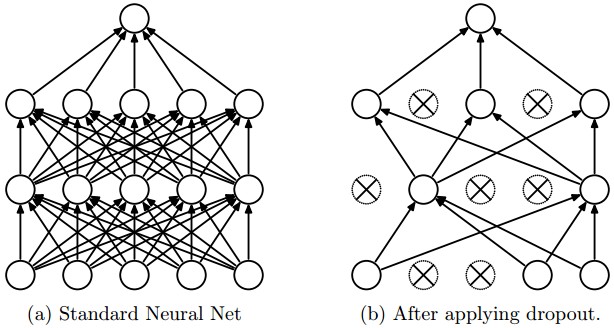
Рисунок, взятый из статьи о выпадении, иллюстрирует эту идею. Во время обучения выпадение можно интерпретировать как выборку нейронной сети из полной нейронной сети и обновление параметров выбранной сети только на основе входных данных. (Однако экспоненциальное количество возможных выбранных сетей не является независимым, поскольку они имеют общие параметры.) Во время тестирования выпадение не применяется, а интерпретируется как оценка усреднённого прогноза по экспоненциально большому ансамблю всех подсетей (подробнее об ансамблях в следующем разделе).
Выпадение в примере трёхслойной нейронной сети будет реализовано следующим образом:
``` """ Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X): """ X contains the data """
# forward pass for example 3-layer neural network H1 = np.maximum(0, np.dot(W1, X) + b1) U1 = np.random.rand(H1.shape) < p # first dropout mask H1 = U1 # drop! H2 = np.maximum(0, np.dot(W2, H1) + b2) U2 = np.random.rand(H2.shape) < p # second dropout mask H2 = U2 # drop! out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown) # perform parameter update... (not shown)
def predict(X): # ensembled forward pass H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations out = np.dot(W3, H2) + b3 ```
В приведённом выше коде внутри функции train_step мы дважды применили отсев: на первом скрытом слое и на втором скрытом слое. Отсев также можно применить непосредственно на входном слое, в этом случае мы также создадим бинарную маску для входных данных X. Обратный проход остаётся неизменным, но, конечно, должен учитывать созданные маски U1,U2.
Важно отметить, что в функции predict мы больше не отбрасываем значения, а выполняем масштабирование выходных значений скрытого слоя с помощью p.Это важно, потому что во время тестирования все нейроны видят все свои входные данные, поэтому мы хотим, чтобы выходные данные нейронов во время тестирования были идентичны ожидаемым выходным данным во время обучения. Например, в случае p=0.5. Нейроны должны вдвое уменьшить свои выходные данные во время тестирования, чтобы получить те же выходные данные, что и во время обучения (в среднем). Чтобы понять это, рассмотрим выходные данные нейрона x (до отбрасывания). При отбрасывании ожидаемый результат от этого нейрона станет px+(1−p)0, потому что выходной сигнал нейрона с вероятностью будет равен нулю 1−p. Во время тестирования, когда мы поддерживаем постоянную активность нейрона, мы должны корректировать x→px, чтобы сохранить ожидаемый результат. Также можно показать, что выполнение этого ослабления во время тестирования может быть связано с процессом перебора всех возможных бинарных масок (и, следовательно, всех экспоненциально большого количества подсетей) и вычисления их совокупного прогноза.
Нежелательным свойством представленной выше схемы является то, что мы должны масштабировать активации по p во время тестирования. Поскольку производительность во время тестирования очень важна, всегда предпочтительнее использовать инвертированное отбрасывание, при котором масштабирование выполняется во время обучения, а прямой проход во время тестирования остаётся нетронутым. Кроме того, это удобно тем, что код прогнозирования может оставаться нетронутым, если вы решите изменить место применения отбрасывания или отказаться от него. Инвертированное отбрасывание выглядит следующим образом:
``` """ Inverted Dropout: Recommended implementation example. We drop and scale at train time and don't do anything at test time. """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X): # forward pass for example 3-layer neural network H1 = np.maximum(0, np.dot(W1, X) + b1) U1 = (np.random.rand(H1.shape) < p) / p # first dropout mask. Notice /p! H1 = U1 # drop! H2 = np.maximum(0, np.dot(W2, H1) + b2) U2 = (np.random.rand(H2.shape) < p) / p # second dropout mask. Notice /p! H2 = U2 # drop! out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown) # perform parameter update... (not shown)
def predict(X): # ensembled forward pass H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary H2 = np.maximum(0, np.dot(W2, H1) + b2) out = np.dot(W3, H2) + b3 ```
После первого появления метода отсева было проведено множество исследований, направленных на то, чтобы понять, в чём заключается его эффективность на практике и как он соотносится с другими методами регуляризации. Рекомендуем ознакомиться с дополнительной литературой для заинтересованных читателей:
- Статья о выпадении из курса Шриваставы и др., 2014.
- Выборочное обучение как адаптивная регуляризация: «мы показываем, что регуляризация с помощью вычеркивания эквивалентна регуляризации \(L_2\) первого порядка, применяемой после масштабирования признаков с помощью оценки обратной диагональной информационной матрицы Фишера».
Тема шума при прямом проходе. Выпадение относится к более общей категории методов, которые вводят стохастическое поведение при прямом проходе сети. Во время тестирования шум усредняется аналитически (как в случае с выпадением при умножении на p) или численно (например, с помощью выборки, выполняя несколько прямых проходов с разными случайными решениями, а затем усредняя их). Примером других исследований в этом направлении является DropConnect, где во время прямого прохода случайный набор весовых коэффициентов устанавливается в ноль. В качестве предвосхищения отметим, что свёрточные нейронные сети также используют эту тему с помощью таких методов, как стохастическое объединение, дробное объединение и увеличение данных. Мы подробно рассмотрим эти методы позже.
Регуляризация смещения. Как мы уже упоминали в разделе о линейной классификации, обычно не рекомендуется регуляризировать параметры смещения, поскольку они не взаимодействуют с данными посредством мультипликативных взаимодействий и, следовательно, не влияют на конечную цель. Однако в практических приложениях (при надлежащей предварительной обработке данных) регуляризация смещения редко приводит к значительному ухудшению производительности. Вероятно, это связано с тем, что по сравнению со всеми весовыми параметрами коэффициентов смещения очень мало, поэтому классификатор может «позволить себе» использовать коэффициенты смещения, если они нужны ему для уменьшения потерь данных.
Послойная регуляризация. Не очень распространена регуляризация разных слоёв с разной степенью (за исключением, возможно, выходного слоя). В литературе опубликовано относительно мало результатов, связанных с этой идеей.
На практике: чаще всего используется единая глобальная сила регуляризации \(L_2\), которая проходит перекрестную проверку. Также часто применяется комбинация с отбрасыванием данных после всех слоев. Значение p=0.5 это разумное значение по умолчанию, но его можно настроить на основе данных проверки.
Функции потерь
Мы обсудили часть целевой функции, отвечающую за регуляризацию, которую можно рассматривать как штраф за определённую меру сложности модели. Вторая часть целевой функции — это потеря данных, которая в задаче обучения с учителем измеряет соответствие между прогнозом (например, оценками классов при классификации) и истинным значением. Потеря данных представляет собой среднее значение потерь данных для каждого отдельного примера. То есть, \(L = \frac{1}{N} \sum_i L_i\) where \(N\), где N - количество обучающих данных. Давайте сократим \(f = f(x_i; W)\) активация выходного слоя в нейронной сети. Существует несколько типов задач, которые вы можете решить на практике:
- Классификация — это случай, который мы подробно обсуждали. Здесь мы предполагаем наличие набора примеров и одной правильной метки (из фиксированного набора) для каждого примера. Одной из двух наиболее часто встречающихся функций стоимости в этой задаче является SVM (например, формулировка Уэстона Уоткинса):
$$
L_i = \sum_{j\neq y_i} \max(0, f_j - f_{y_i} + 1)
$$
Как мы вкратце упомянули, некоторые люди сообщают о более высокой производительности при использовании квадратичной функции потерь (т. е. вместо \(\max(0, f_j - f_{y_i} + 1)^2\)). Вторым распространенным выбором является классификатор Softmax, который использует кросс-энтропийные потери:
$$
L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right)
$$
Проблема: большое количество классов. Когда набор меток очень велик (например, слова в английском словаре или ImageNet, содержащий 22 000 категорий), вычисление полной вероятности по методу Softmax становится дорогостоящим. Для некоторых приложений популярны приближённые версии. Например, в задачах обработки естественного языка может быть полезно использовать иерархический Softmax (см. одно из объяснений здесь (pdf)).
Иерархический Softmax раскладывает слова на метки в виде дерева. Затем каждая метка представляется в виде пути по дереву, и в каждом узле дерева обучается классификатор Softmax, чтобы различать левую и правую ветви. Структура дерева сильно влияет на производительность и, как правило, зависит от задачи.
-
Классификация атрибутов. Оба приведённых выше примера предполагают, что существует единственный правильный ответ \(y_i\). Но что , если \(y_i\)- это бинарный вектор, в котором каждый пример может иметь или не иметь определённый атрибут, и где атрибуты не исключают друг друга? Например, изображения Вконтакте можно рассматривать как помеченные определённым подмножеством хэштегов из большого набора всех хэштегов, и изображение может содержать несколько хэштегов. Разумным подходом в этом случае будет создание бинарного классификатора для каждого отдельного атрибута. Например, бинарный классификатор для каждой категории отдельно будет иметь вид:
$$ L_i = \sum_j \max(0, 1 - y_{ij} f_j) $$
где сумма по всем категориям \(j\) и \(y_{ij}\) равно +1 или -1 в зависимости от того, помечен ли i-й пример j-м атрибутом, а вектор оценки \(f_j\) будет положительным, если класс прогнозируется как присутствующий, и отрицательным в противном случае. Обратите внимание, что потери накапливаются, если положительный пример имеет оценку меньше +1 или если отрицательный пример имеет оценку больше -1.
Альтернативой этому подходу было бы обучение классификатора логистической регрессии для каждого атрибута по отдельности. Бинарный классификатор логистической регрессии имеет только два класса (0, 1) и вычисляет вероятность класса 1 следующим образом:
$$ P(y = 1 \mid x; w, b) = \frac{1}{1 + e^{-(w^Tx +b)}} = \sigma (w^Tx + b) $$
Поскольку сумма вероятностей классов 1 и 0 равна единице, вероятность класса 0 равна \(P(y = 0 \mid x; w, b) = 1 - P(y = 1 \mid x; w,b)\). Таким образом, пример классифицируется как положительный (y = 1), если \(\sigma (w^Tx + b) > 0.5\), или что эквивалентно , если оценка \(w^Tx +b > 0\). Затем функция потерь максимизирует эту вероятность. Вы можете убедиться, что это сводится к минимизации отрицательного логарифма правдоподобия:
$$ L_i = -\sum_j y_{ij} \log(\sigma(f_j)) + (1 - y_{ij}) \log(1 - \sigma(f_j)) $$
где этикетки \(y_{ij}\) считаются равными либо 1 (положительному), либо 0 (отрицательному), и \(\sigma(\cdot)\). Это сигмоидальная функция. Приведённое выше выражение может показаться пугающим, но градиент на f на самом деле он чрезвычайно прост и интуитивно понятен: \(\partial{L_i} / \partial{f_j} = \sigma(f_j) - y_{ij}\) (поскольку вы можете перепроверить себя, взяв производные). -
Регрессия — это задача прогнозирования величин с действительными значениями, таких как цена дома или длина чего-либо на изображении. Для решения этой задачи обычно вычисляют потери между прогнозируемой величиной и истинным ответом, а затем измеряют норму \(L_2\) в квадрате или норму \(L_1\) разности. Норма \(L_2\) в квадрате вычисляет потери для одного примера в виде:
$$ L_i = \Vert f - y_i \Vert_2^2 $$
Причина, по которой норма \(L_2\) возводится в квадрат в целевой функции, заключается в том, что градиент становится намного проще, не меняя оптимальные параметры, поскольку возведение в квадрат — это монотонная операция. Норма \(L_1\) вычисляется путём суммирования абсолютных значений по каждому измерению:
$$ L_i = \Vert f - y_i \Vert_1 = \sum_j \mid f_j - (y_i)j \mid $$
_где сумма__ \(\sum_j\) это сумма по всем параметрам желаемого прогноза, если прогнозируется более одной величины. Рассмотрим только j-й параметр i-го примера и обозначим разницу между истинным и прогнозируемым значением как \(\delta_{ij}\), градиент для этого измерения (т.е. \(\partial{L_i} / \partial{f_j}\))) легко выводится как либо \(\delta_{ij}\) с нормой \(L_2\), или \(sign(\delta_{ij})\).То есть градиент оценки будет либо прямо пропорционален разнице в ошибках, либо будет фиксированным и унаследует только знак разницы.
_Предупреждение: важно отметить, что функцию потерь \(L_2\) гораздо сложнее оптимизировать, чем более стабильную функцию потерь, такую как Softmax.
Интуитивно понятно, что для этого требуется очень хрупкое и специфическое свойство сети, чтобы она выдавала ровно одно правильное значение для каждого входного сигнала (и его расширений). Обратите внимание, что это не относится к Softmax, где точное значение каждого балла менее важно: важно только, чтобы их величины были соответствующими. Кроме того, функция потерь \(L_2\) менее устойчива, поскольку выбросы могут приводить к огромным градиентам. Столкнувшись с проблемой регрессии, сначала подумайте, абсолютно ли недостаточно квантовать выходные данные по ячейкам. Например, если вы прогнозируете звездный рейтинг продукта, возможно, гораздо лучше использовать 5 независимых классификаторов для оценок в 1-5 звезд вместо потери регрессии. Классификация имеет дополнительное преимущество в том, что она может дать вам распределение по результатам регрессии, а не только по одному результату без указания его достоверности. Если вы уверены, что классификация не подходит, используйте \(L_2\), но будьте осторожны: например, \(L_2\) более нестабилен, и применять отсев в сети (особенно на слое непосредственно перед потерей \(L_2\)) — не лучшая идея.
Сталкиваясь с задачей регрессии, в первую очередь подумайте, действительно ли она необходима. Вместо этого по возможности дискретизируйте выходные данные и выполняйте классификацию по ним.
- Структурированное прогнозирование. Структурированные потери относятся к случаю, когда метками могут быть произвольные структуры, такие как графы, деревья или другие сложные объекты. Обычно также предполагается, что пространство структур очень велико и его нелегко перебрать. Основная идея структурированных потерь SVM заключается в том, чтобы требовать запас между правильной структурой и \(y_i\) и набравшая наибольшее количество баллов неправильная структура. Эту проблему не принято решать как простую задачу неограниченной оптимизации с градиентным спуском. Вместо этого обычно разрабатываются специальные решатели, позволяющие воспользоваться конкретными упрощающими допущениями структурного пространства. Мы кратко упоминаем проблему, но считаем, что специфика выходит за рамки данного класса.
Краткая сводка
Подводя итог:
- Рекомендуется предварительно обработать данные, чтобы их среднее значение было равно нулю, и нормализовать их масштаб до [-1, 1] по каждому признаку
- Инициализируйте веса, извлекая их из гауссова распределения со стандартным отклонением \(\sqrt{2/n}\), where \(n\), где n - это количество входов в нейрон. Например, в NumPy: w = np.random.randn(n) * sqrt(2.0/n).
- Используйте регуляризацию \(L_2\) и отсев (перевернутая версия)
- Используйте пакетную нормализацию
- Мы обсудили различные задачи, которые вы можете выполнять на практике, и наиболее распространённые функции потерь для каждой задачи
Теперь мы предварительно обработали данные, настроили и инициализировали модель. В следующем разделе мы рассмотрим процесс обучения и его динамику.