Обучение нейронных сетей

Обучение нейронных сетей

Содержание: - Проверка градиента - Проверки здравомыслия - Присмотр за процессом обучения - Функция потерь - Точность поезда/вала - Соотношение весов:обновлений - Распределение активации/градиента на слой - Визуализация - Обновление параметров - Первый порядок (SGD), импульс, импульс Нестерова - Отжиг темпов обучения - Методы второго порядка - Дополнительные материалы - Методы адаптивной скорости обучения для каждого параметра (Adagrad, RMSProp) - Оптимизация гиперпараметров - Оценка - Модельные ансамбли - Краткая сводка - Дополнительные материалы

Обучение

В предыдущих разделах мы рассмотрели статические части нейронных сетей: как мы можем настроить сетевую связность, данные и функцию потерь. Этот раздел посвящен динамике, или другими словами, процессу изучения параметров и нахождения хороших гиперпараметров.

Проверка градиента

Теоретически выполнить проверку градиента так же просто, как сравнить аналитический градиент с числовым градиентом. На практике этот процесс гораздо более сложный и подвержен ошибкам. Вот несколько советов, рекомендаций и проблем, на которые следует обратить внимание:

Используйте формулу по центру. Формула, которую вы, возможно, видели для приближения конечных разностей при вычислении численного градиента, выглядит следующим образом:

$$ \frac{df(x)}{dx} = \frac{f(x + h) - f(x)}{h} \hspace{0.1in} \text{(bad, do not use)} $$

где h это очень небольшое число, на практике примерно 1e-5 или около того. На практике оказывается, что гораздо лучше использовать формулу центрированной разности вида:

$$ \frac{df(x)}{dx} = \frac{f(x + h) - f(x - h)}{2h} \hspace{0.1in} \text{(use instead)} $$

Для этого вам придется дважды оценить функцию потерь, чтобы проверить каждое измерение градиента (так что это примерно в 2 раза дороже), но аппроксимация градиента оказывается гораздо более точной. Чтобы убедиться в этом, можно использовать разложение Тейлора \(f(x+h)\) и \(f(x-h)\) и убедитесь, что первая формула содержит ошибку порядка O(h), в то время как вторая формула содержит только члены ошибки порядка \(O(h^2)\) (т.е. это приближение второго порядка).

Используйте относительную погрешность для сравнения. В чем особенности сравнения численного градиента \(f'_n\) и аналитический градиент \(f'_a\)? То есть, как мы узнаем, что они несовместимы? У вас может возникнуть соблазн отслеживать разницу \(\mid f'_a - f'_n \mid \) или его квадрат и определите проверку градиента как неудачную, если эта разница превышает пороговое значение. Однако это проблематично. Для примера рассмотрим случай, когда их разница равна 1e-4. Это кажется очень подходящей разницей, если два градиента близки к 1.0, поэтому мы считаем, что два градиента совпадают. Но если бы оба градиента были порядка 1e-5 или ниже, то мы бы считали 1e-4 огромной разницей и, скорее всего, неудачей. Следовательно, всегда более уместно учитывать относительную ошибку:

$$ \frac{\mid f'_a - f'_n \mid}{\max(\mid f'_a \mid, \mid f'_n \mid)} $$

которая рассматривает отношение их разностей к отношению абсолютных значений обоих градиентов. Обратите внимание, что обычно формула относительной ошибки включает только один из двух членов (любой из них), но я предпочитаю увеличивать (или добавлять) оба, чтобы сделать его симметричным и предотвратить деление на ноль в случае, когда одно из двух равно нулю (что часто случается, особенно с ReLU). Тем не менее, необходимо явно отслеживать случай, когда оба равны нулю, и пройти проверку градиента в этом крайнем случае. На практике:
- Относительная погрешность > 1e-2 обычно означает, что градиент, вероятно, неправильный - 1e-2 > относительная погрешность > 1e-4 должна заставить вас чувствовать себя некомфортно - 1e-4 > относительная погрешность обычно приемлема для целей с изломами. Но если нет перегибов (например, использование нелинейностей tanh и softmax), то 1e-4 слишком велико. - 1e-7 и меньше вы должны быть счастливы.

Также имейте в виду, что чем глубже сеть, тем выше будут относительные ошибки. Таким образом, если вы проверяете входные данные для 10-слойной сети, относительная ошибка 1e-2 может быть нормальной, потому что ошибки накапливаются по мере прохождения. И наоборот, ошибка 1e-2 для одной дифференцируемой функции, скорее всего, указывает на неправильный градиент.

Используйте двойную точность. Распространенной ошибкой является использование плавающей точки одинарной точности для вычисления проверки градиента. Часто бывает так, что вы можете получить высокие относительные ошибки (до 1e-2) даже при правильной реализации градиента. По моему опыту, я иногда видел, как мои относительные ошибки резко уменьшались с 1e-2 до 1e-8 при переходе на двойную точность.

Оставайтесь в активном диапазоне плавающей запятой. Хорошей идеей будет прочитать статью «Что каждый специалист по информатике должен знать об арифметике с плавающей запятой», так как это может развеять мифы об ошибках и позволить вам писать более тщательный код. Например, в нейронных сетях может быть распространена нормализация функции потерь по пакету.

Однако, если градиенты для каждой точки данных очень малы, то дополнительное деление их на количество точек данных начинает давать очень маленькие числа, что, в свою очередь, приведет к большему количеству числовых проблем. Вот почему я предпочитаю всегда печатать исходный числовой/аналитический градиент и следить за тем, чтобы числа, которые вы сравниваете, не были слишком маленькими (например, примерно 1e-10 и меньше по абсолютному значению вызывает беспокойство). Если это так, вы можете временно масштабировать функцию потерь на константу, чтобы привести их к "более хорошему" диапазону, где числа с плавающей запятой более плотные - в идеале порядка 1,0, где экспонента с плавающей запятой равна 0.

Изгибы в достижении цели. Одним из источников неточностей, о которых следует знать при проверке градиента, является проблема изгибов. Изгибы относятся к недифференцируемым частям целевой функции, вводимым такими функциями, как ReLU (\(max(0,x)\)) ) или потеря SVM, нейроны Maxout и т.д. Рассмотрим градиентную проверку функции ReLU по адресу \(x = -1e6\). С \(x < 0\), аналитический градиент в этой точке равен нулю. Однако числовой градиент внезапно вычислит ненулевой градиент, потому что \(f(x+h)\) может пересечь излом (например, если \(h > 1e-6\) ) и ввести ненулевой взнос. Вы можете подумать, что это патологический случай, но на самом деле этот случай может быть очень распространенным. Например, СВМ для CIFAR-10 содержит до 450 000 (\(max(0,x)\)) термины, потому что существует 50 000 примеров, и каждый пример дает 9 терминов для цели. Более того, нейронная сеть с классификатором SVM будет содержать гораздо больше изломов из-за ReLU.

Обратите внимание, что можно узнать, был ли пересечен излом при оценке убытка. Это можно сделать, отслеживая личности всех «победителей» в функции формы (\(max(0,x)\)); То есть был x или y выше во время паса вперед. Если при оценке изменилась личность хотя бы одного победителя \(f(x+h)\), а в последствии \(f(x-h)\), то был пересечен излом и числовой градиент не будет точным.

Используйте только несколько точек данных. Одним из решений вышеупомянутой проблемы перегибов является использование меньшего количества точек данных, поскольку функции потерь, которые содержат перегибы (например, из-за использования ReLU или маржинальных потерь и т. д.), будут иметь меньше перегибов с меньшим количеством точек данных, поэтому вероятность того, что вы пересечете одну из них, при выполнении конечного другого приближения, снижается. Более того, если ваш gradcheck всего на ~2 или 3 точки данных, то вы почти наверняка проверите весь пакет. Использование очень небольшого количества точек данных также делает проверку градиента быстрее и эффективнее.

Будьте осторожны с размером шага h. Не обязательно минимальный размер h- это хорошо, так как в таком случае есть шанс напороться на проблему численной точности. Иногда, при проверке корректности градиента h, возможно, что значение 1е-4 и 1е-6 будет изменяться от абсолютно неверному при увеличении этого показателя. Эта статья в Википедии содержит диаграмму, которая отображает значение h по оси x и числовую ошибку градиента по оси y.

Градусная проверка во время «характерного» режима работы. Важно понимать, что проверка градиента выполняется в определенной (и обычно случайной), единственной точке в пространстве параметров. Даже если проверка градиента на этом этапе выполнена успешно, не сразу можно быть уверенным в том, что градиент правильно реализован глобально. Кроме того, случайная инициализация может быть не самой «характерной» точкой в пространстве параметров и фактически может привести к патологическим ситуациям, когда градиент кажется правильно реализованным, но на самом деле это не так. Например, SVM с очень малой инициализацией веса присвоит почти ровно нулевые оценки всем точкам данных, а градиенты будут демонстрировать определенную закономерность во всех точках данных. Неправильная реализация градиента все равно может привести к появлению этого шаблона и не привести к более характерному режиму работы, в котором одни баллы больше других. Поэтому, чтобы быть в безопасности, лучше всего использовать короткое время прогорания, в течение которого сеть может обучиться и выполнить градиентную проверку после того, как потери начнут снижаться. Опасность его выполнения на первой итерации заключается в том, что это может привести к патологическим пограничным случаям и замаскировать неправильную реализацию градиента.

Не позволяйте регуляризации перегружать данные. Часто бывает так, что функция потерь является суммой потерь данных и потерь от регуляризации (например, штраф \(L_2\) за веса). Одна из опасностей, о которой следует знать, заключается в том, что потеря регуляризации может превзойти потерю данных, и в этом случае градиенты будут в основном исходить от члена регуляризации (который обычно имеет гораздо более простое выражение градиента). Это может замаскировать неправильную реализацию градиента потери данных. Поэтому рекомендуется отключить регуляризацию и проверять сначала только потерю данных, а затем второй и независимый термин регуляризации. Одним из способов выполнения последнего является взлом кода, чтобы устранить вклад потери данных. Другой способ состоит в том, чтобы увеличить силу регуляризации, чтобы гарантировать, что ее эффектом не будет пренебрежение при проверке градиента, и что будет замечена неправильная реализация.

Не забудьте отключить выпадение/аугментации. Выполняя градиентную проверку, не забывайте отключать любые недетерминированные эффекты в сети, такие как выпадение, случайные аугментации данных и т. д. В противном случае это может привести к огромным ошибкам при оценке численного градиента. Недостатком отключения этих эффектов является то, что вы не будете проверять их градиент (например, может случиться так, что выпадение не будет правильно распространено). Следовательно, лучшим решением может быть принудительное использование определенного случайного начального значения перед оценкой обоих \(f(x+h)\) и \(f(x-h)\), а также при оценке аналитического градиента.

Проверьте только несколько размеров. На практике градиенты могут иметь размеры в миллион параметров. В этих случаях целесообразно проверить только некоторые размеры градиента и предположить, что другие являются правильными. Будьте внимательны: Один из вопросов, с которым следует быть осторожным, заключается в том, чтобы убедиться, что градиент проверяет несколько размеров для каждого отдельного параметра. В некоторых приложениях люди объединяют параметры в один большой вектор параметров для удобства. В этих случаях, например, смещения могут занимать лишь небольшое количество параметров из всего вектора, поэтому важно не выбирать случайным образом, а учитывать это и проверять, что все параметры получают правильные градиенты.

Перед изучением: советы и рекомендации по проверке здравомыслия

Вот несколько проверок здравого смысла, которые вы могли бы провести, прежде чем погрузиться в дорогостоящую оптимизацию: - Ищите правильный проигрыш при случайном исполнении. Убедитесь, что вы получаете ожидаемые потери при инициализации с небольшими параметрами. Лучше всего сначала проверить только потерю данных (поэтому установите интенсивность регуляризации равной нулю). Например, для CIFAR-10 с классификатором Softmax мы ожидаем, что начальный убыток составит 2,302, потому что мы ожидаем диффузную вероятность 0,1 для каждого класса (поскольку классов 10), а Softmax убыток — это отрицательная логарифмическая вероятность правильного класса, таким образом: -ln(0,1) = 2,302. Для The Weston Watkins SVM мы ожидаем, что все желаемые маржи будут нарушены (поскольку все баллы примерно равны нулю), и, следовательно, ожидаем потери 9 (поскольку маржа равна 1 для каждого неправильного класса). Если вы не видите этих потерь, возможно, возникла проблема с инициализацией.

• В качестве второй проверки здравомыслия, увеличение силы регуляризации должно привести к увеличению потерь
• Переобучение крошечного подмножества данных. И последнее, и самое важное, прежде чем обучаться на полном наборе данных, попытайтесь обучиться на крошечной части (например, на 20 примерах) ваших данных и убедитесь, что вы можете достичь нулевой стоимости. Для этого эксперимента также лучше всего установить регуляризацию равной нулю, иначе это может помешать получению нулевой стоимости. Если вы не пройдете эту проверку на здравомыслие с небольшим набором данных, не стоит переходить к полному набору данных. Обратите внимание, что может случиться так, что вы можете переобучать очень маленький набор данных, но все равно иметь неправильную реализацию. Например, если признаки точек данных являются случайными из-за какой-либо ошибки, то можно перенаучить небольшой обучающий набор, но вы никогда не заметите обобщения при свертывании всего набора данных.

Присмотр за процессом обучения

Существует множество полезных величин, которые вы должны отслеживать во время обучения нейронной сети. Эти графики являются окном в процесс обучения и должны использоваться для получения интуиции о различных настройках гиперпараметров и о том, как их следует изменить для более эффективного обучения.

Ось x приведенных ниже графиков всегда указывается в единицах эпох, которые измеряют, сколько раз каждый пример был замечен во время обучения в ожидании (например, одна эпоха означает, что каждый пример был просмотрен один раз). Предпочтительнее отслеживать эпохи, а не итерации, так как количество итераций зависит от произвольной настройки размера пакета.

Функция потерь

Первая величина, которую полезно отслеживать во время тренировки, — это потери, так как они оцениваются по отдельным партиям во время паса вперед. Ниже приведена мультяшная диаграмма, показывающая потери с течением времени, и особенно то, что форма может рассказать вам о скорости обучения:

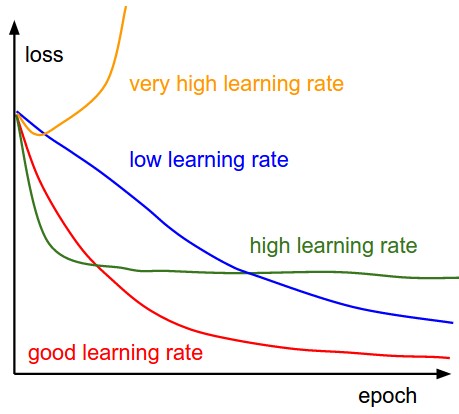
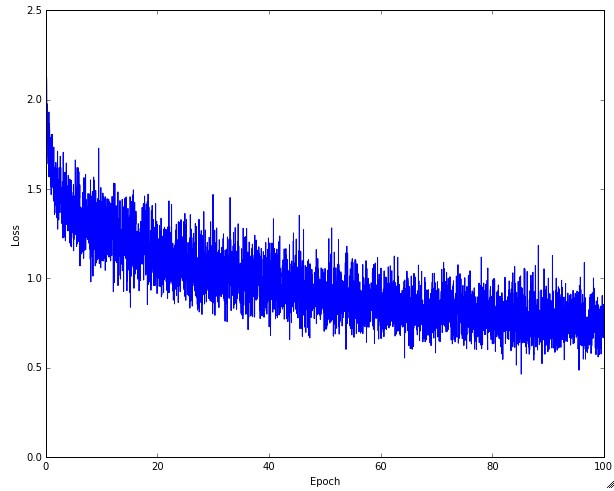
Сверху: Мультфильм, изображающий эффекты различных скоростей обучения. При низких темпах обучения улучшения будут линейными. С высокими темпами обучения они начнут выглядеть более экспоненциально. Более высокие темпы обучения будут уменьшать потери быстрее, но они застревают на худших значениях потерь (зеленая линия). Это связано с тем, что в оптимизации слишком много «энергии», а параметры хаотично колеблются, не в силах занять хорошее место в ландшафте оптимизации. Снизу: Пример типичной функции потерь во времени при обучении небольшой сети на наборе данных CIFAR-10. Эта функция потерь выглядит разумной (она может указывать на слишком маленькую скорость обучения, основанную на скорости распада, но трудно сказать), а также указывает на то, что размер партии может быть слишком низким (поскольку стоимость слишком зашумлена).

Величина «покачивания» в потерях связана с размером партии. Когда размер партии равен 1, покачивание будет относительно большим. Если размер пакета равен полному набору данных, покачивание будет минимальным, так как каждое обновление градиента должно монотонно улучшать функцию потерь (если только скорость обучения не установлена слишком высокой).

Некоторые пользователи предпочитают строить графики своих функций потерь в области журнала. Поскольку прогресс в обучении обычно принимает экспоненциальную форму, график выглядит как чуть более интерпретируемая прямая линия, а не как хоккейная клюшка. Кроме того, если на одном и том же графике потерь построить несколько моделей с перекрестной проверкой, различия между ними становятся более очевидными.

Иногда функции проигрыша могут выглядеть забавно lossfunctions.tumblr.com.

Точность поезда/вала

Вторая важная величина, которую необходимо отслеживать при обучении классификатора, — это точность валидации/обучения. Этот график может дать вам ценную информацию о количестве переобучения в вашей модели:

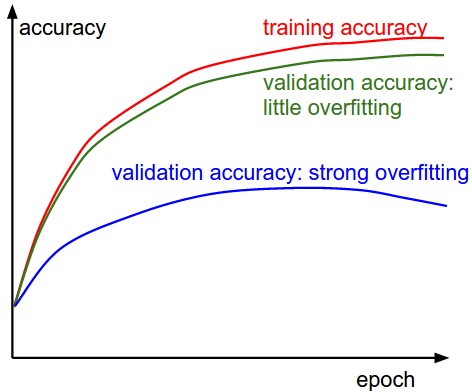
Разрыв между точностью обучения и валидации указывает на степень переобучения. Два возможных случая показаны на схеме слева. Синяя кривая ошибок валидации показывает очень низкую точность валидации по сравнению с точностью обучения, что указывает на сильное переобучение (обратите внимание, что точность валидации может даже начать снижаться после какого-то момента). Когда вы видите это на практике, вы, вероятно, захотите увеличить регуляризацию (сильнее штраф в весе \(L_2\), больше отсева и т.д.) или собрать больше данных. Другой возможный случай — когда точность валидации достаточно хорошо отслеживает точность обучения. Этот случай указывает на то, что емкость вашей модели недостаточно высока: увеличьте модель, увеличив количество параметров.

Соотношение весов:обновления

Последняя величина, которую вы, возможно, захотите отслеживать, — это отношение величин обновления к величине значений. Примечание: обновления, а не исходные градиенты (например, в ванильном sgd это будет градиент, умноженный на скорость обучения). Возможно, вы захотите оценить и отследить это соотношение для каждого набора параметров независимо. Грубая эвристика заключается в том, что это соотношение должно быть где-то в районе 1e-3. Если он ниже, то скорость обучения может быть слишком низкой. Если он выше, то, скорее всего, уровень обучения слишком высок. Вот конкретный пример:

# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3

Вместо того, чтобы отслеживать минимальное или максимальное значение, некоторые люди предпочитают вычислять и отслеживать норму градиентов и их обновлений. Эти метрики обычно коррелируют и часто дают примерно одинаковые результаты.

Распределение активации/градиента на слой

Неправильная инициализация может замедлить или даже полностью затормозить процесс обучения. К счастью, эту проблему можно диагностировать относительно легко. Одним из способов сделать это является построение гистограмм активации/градиента для всех слоев сети. Интуитивно понятно, что не очень хорошо видеть какие-либо странные распределения - например, с нейронами tanh мы хотели бы видеть распределение активаций нейронов между полным диапазоном [-1,1], вместо того, чтобы видеть, как все нейроны выдают ноль, или все нейроны полностью насыщаются либо при -1, либо при 1.

Визуализации первого уровня

Наконец, при работе с пикселями изображения может быть полезно и приятно визуально отобразить объекты первого слоя:

Примеры визуализированных весов для первого слоя нейронной сети. Сверху: Зашумленные функции указывают на то, что симптомом может быть неконвергентная сеть, неправильно установленная скорость обучения, очень низкий вес штрафа за регуляризацию. Снизу: Красивые, гладкие, чистые и разнообразные черты лица являются хорошим признаком того, что тренировка идет хорошо.

Обновление параметров

После вычисления аналитического градиента с помощью обратного распространения градиенты используются для обновления параметров. Существует несколько подходов к выполнению обновления, о которых мы поговорим далее.

Отметим, что оптимизация для глубоких сетей в настоящее время является очень активным направлением исследований. В этом разделе мы выделим некоторые устоявшиеся и распространенные техники, которые вы можете увидеть на практике, кратко опишем их интуицию, но оставим подробный разбор за рамками занятия. Мы даем несколько дополнительных указаний для заинтересованного читателя.

Первый порядок (SGD), импульс, импульс Нестерова

Ванильное обновление. Простейшей формой обновления является изменение параметров в направлении отрицательного градиента (поскольку градиент указывает направление увеличения, но обычно мы хотим минимизировать функцию потерь). Предполагая вектор параметров и градиент, простейшее обновление имеет вид:x dx

# Vanilla update
x += - learning_rate * dx

где гиперпараметр - фиксированная константа. При оценке на полном наборе данных и при достаточно низкой скорости обучения это гарантированно приведет к неотрицательному прогрессу в функции потерь.learning_rate

Обновление импульса (Momentum update) — еще один подход, который почти всегда имеет более высокую скорость сходимости в глубоких сетях. Это обновление может быть мотивировано с физической точки зрения задачи оптимизации. В частности, потери можно интерпретировать как высоту холмистой местности (и, следовательно, также как потенциальную энергию, так как U=mgh. И поэтому \( U \propto h \) ). Инициализация параметров случайными числами эквивалентна установке частицы с нулевой начальной скоростью в каком-либо месте. В этом случае процесс оптимизации можно рассматривать как эквивалент процесса моделирования вектора параметров (т.е. частицы) как движущейся по ландшафту.

Поскольку сила, действующая на частицу, связана с градиентом потенциальной энергии (т.е. F=−∇U ), сила, ощущаемая частицей, в точности является (отрицательным) градиентом функции потерь. Сверх того F=ma. Таким образом, (отрицательный) градиент с этой точки зрения пропорционален ускорению частицы. Обратите внимание, что это отличается от показанного выше обновления SGD, где градиент напрямую интегрирует положение. Вместо этого физический взгляд предлагает обновление, в котором градиент только напрямую влияет на скорость, что, в свою очередь, влияет на положение:

```

Momentum update

v = mu * v - learning_rate * dx # integrate velocity x += v # integrate position

Здесь мы видим введение переменной `v`, которая инициализируется нулем, и дополнительный гиперпараметр (`mu`). К сожалению, эта переменная в оптимизации называется _импульсом_ (ее типичное значение составляет около **0,9**), но ее физическое значение больше соответствует коэффициенту трения. По сути, эта переменная гасит скорость и снижает кинетическую энергию системы, иначе частица никогда бы не остановилась у подножия холма. При перекрестной проверке этому параметру обычно присваиваются такие значения, как **[0.5, 0.9, 0.95, 0.99]**. Подобно графикам отжига для темпов обучения (*обсуждается ниже*), оптимизация иногда может немного выиграть от графиков импульса, где импульс увеличивается на более поздних этапах обучения. Типичная настройка заключается в том, чтобы начать с импульса около **0,5** и отжечь его до **0,99** или около того в течение нескольких эпох.`v` `mu`  

>При обновлении Momentum вектор параметра будет наращивать скорость в любом направлении, которое имеет постоянный градиент.  

__Импульс Нестерова__ (*Nesterov Momentum*) – это немного другая версия обновления *Momentum*, которое в последнее время набирает популярность. Он обладает более сильными теоретическими гарантиями сходимости для выпуклых функций и на практике также стабильно работает немного лучше стандартного импульса.  

Основная идея метода Нестерова заключается в том, что когда текущий вектор параметров находится в некотором положении `x`, то, глядя на приведённое выше обновление импульса, мы знаем, что только импульс (то есть без учёта второго слагаемого с градиентом) должен сдвинуть вектор параметров на `mu * v`. Поэтому, если мы собираемся вычислить градиент, мы можем рассматривать будущее приблизительное положение `x + mu * v` как «забежание вперёд» — это точка в окрестности того места, где мы вскоре окажемся. Следовательно, имеет смысл вычислять градиент в `x + mu * v` вместо «старой/устаревшей» позиции `x`.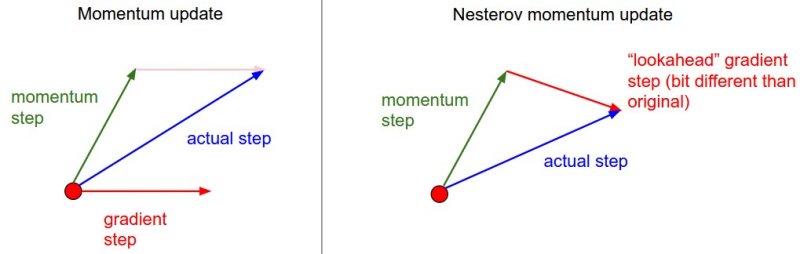  
___  

  ![](https://cs231n.github.io/assets/nn3/nesterov.jpeg)  

Нестеровский импульс. Вместо того, чтобы оценивать градиент в текущем положении (красный круг), мы знаем, что наш импульс вот-вот приведет нас к кончику зеленой стрелки. Таким образом, с помощью импульса Нестерова мы оцениваем градиент в этой «просматриваемой» позиции.  
  ___  

То есть, в немного неудобной нотации, мы хотели бы сделать следующее:  

  ```
  x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

Однако на практике люди предпочитают выражать обновление так, чтобы оно было максимально похоже на ванильный SGD или на предыдущее импульсное обновление. Этого можно достичь, манипулируя приведенным выше обновлением с помощью переменной transform , а затем выражая обновление в терминах вместо . То есть, вектор параметров, который мы на самом деле сохраняем, всегда является опережающей версией. Уравнения в терминах (но переименовывая его обратно в ) становятся такими:x_ahead = x + mu * v x_ahead x x_ahead x

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

Мы рекомендуем эту дополнительную литературу, чтобы понять источник этих уравнений и математическую формулировку ускоренного импульса Нестерова (NAG):

Отжиг темпов обучения

При обучении глубоких сетей обычно полезно отжигать скорость обучения с течением времени. Хорошая интуиция заключается в том, что при высокой скорости обучения система содержит слишком много кинетической энергии, и вектор параметров хаотично скачет, не имея возможности оседать в более глубоких, но более узких частях функции потерь. Понять, когда нужно снижать скорость обучения, может быть непросто: снижайте ее медленно, и вы будете тратить впустую вычисления, хаотично прыгая с небольшим улучшением в течение длительного времени. Но если загнить слишком агрессивно, система охладится слишком быстро, не сумев достичь наилучшего положения. Существует три распространенных типа реализации снижения скорости обучения:

• Шаг затухания: Уменьшайте скорость обучения в несколько раз каждые несколько эпох. Типичными значениями могут быть снижение скорости обучения вдвое каждые 5 эпох или на 0,1 каждые 20 эпох. Эти цифры в значительной степени зависят от типа задачи и модели. Одна из эвристик, которую вы можете увидеть на практике, заключается в том, чтобы наблюдать за ошибкой валидации во время обучения с фиксированной скоростью обучения и уменьшать скорость обучения на константу (например, 0,5) всякий раз, когда ошибка валидации перестает улучшаться.

• Экспоненциальный затухание. имеет математическую форму \(\alpha = \alpha_0 e^{-k t}\), где \(\alpha_0, k\) являются гиперпараметрами и t — номер итерации (но можно использовать и единицы измерения эпох).

• Распад на 1/т имеет математический вид \(\alpha = \alpha_0 / (1 + k t )\), где \(a_0, k\) являются гиперпараметрами и t — номер итерации.

На практике мы обнаруживаем, что шаг затухания немного предпочтительнее, потому что связанные с ним гиперпараметры (доля затухания и время шага в единицах эпох) более интерпретируемы, чем гиперпараметр k. Наконец, если вы можете позволить себе вычислительный бюджет, ошибитесь в сторону более медленного распада и тренируйтесь в течение более длительного времени.

Методы второго порядка

Вторая, популярная группа методов оптимизации в контексте глубокого обучения основана на методе Ньютона, который повторяет следующее обновление:

$$ x \leftarrow x - [H f(x)]^{-1} \nabla f(x) $$

Здесь Hf(x) — матрица Гессена, представляющая собой квадратную матрицу частных производных функции второго порядка. Термин ∇f(x)— вектор градиента, как показано в Gradient Descent. Интуитивно гессенский метод описывает локальную кривизну функции потерь, что позволяет нам выполнить более эффективное обновление. В частности, умножение на обратное гессенское значение приводит к тому, что оптимизация делает более агрессивные шаги в направлениях малой кривизны и более короткие шаги в направлениях крутой кривизны. Обратите внимание, что особенно важно, на отсутствие каких-либо гиперпараметров скорости обучения в формуле обновления, что сторонники этих методов называют большим преимуществом по сравнению с методами первого порядка.

Тем не менее, приведенное выше обновление непрактично для большинства приложений глубокого обучения, потому что вычисление (и инвертирование) гессена в его явной форме является очень дорогостоящим процессом как в пространстве, так и во времени. Например, нейронная сеть с одним миллионом параметров будет иметь гессенову матрицу размером [1 000 000 x 1 000 000], занимающую примерно 3725 гигабайт оперативной памяти. Следовательно, было разработано большое разнообразие квазиньютоновских методов, которые стремятся аппроксимировать обратный гессенский метод. Среди них наиболее популярным является L-BFGS, который использует информацию в градиентах с течением времени для неявного формирования аппроксимации (т.е. полная матрица никогда не вычисляется).

Тем не менее, даже после того, как мы устраним проблемы с памятью, большим недостатком наивного применения L-BFGS является то, что его приходится вычислять по всему обучающему набору, который может содержать миллионы примеров. В отличие от мини-партий SGD, заставить L-BFGS работать с мини-партиями сложнее и является активной областью исследований.

На практике в настоящее время не часто можно увидеть, чтобы L-BFGS или аналогичные методы второго порядка применялись к крупномасштабному глубокому обучению и сверточным нейронным сетям. Вместо этого варианты SGD, основанные на импульсе (Нестерова), более стандартны, потому что они проще и легче масштабируются.

Дополнительные материалы:

• Large Scale Distributed Deep Networks — это статья от команды Google Brain, в которой сравниваются варианты L-BFGS и SGD в крупномасштабной распределенной оптимизации.
• Алгоритм SFO стремится объединить преимущества SGD с преимуществами L-BFGS.

Методы адаптивной скорости обучения для каждого параметра

Все предыдущие подходы, которые мы обсуждали до сих пор, манипулировали скоростью обучения глобально и одинаково по всем параметрам. Настройка скорости обучения — дорогостоящий процесс, поэтому много работы было потрачено на разработку методов, которые могут адаптивно настраивать скорость обучения и даже делать это для каждого параметра. Многие из этих методов могут по-прежнему требовать других настроек гиперпараметров, но аргумент заключается в том, что они хорошо работают для более широкого диапазона значений гиперпараметров, чем скорость необработанного обучения. В этом разделе мы выделим некоторые распространенные адаптивные методы, с которыми вы можете столкнуться на практике:

Adagrad — это метод адаптивной скорости обучения, первоначально предложенный Дучи и др.

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

Обратите внимание, что переменная имеет размер, равный размеру градиента, и отслеживает сумму квадратов градиентов по каждому параметру. Затем это используется для нормализации шага обновления параметров по элементам. Обратите внимание, что для весов, получающих высокие градиенты, эффективная скорость обучения будет снижена, в то время как для весов, получающих небольшие или нечастые обновления, эффективная скорость обучения будет увеличена. Забавно, но операция извлечения квадратного корня оказывается очень важной, и без нее алгоритм работает гораздо хуже. Сглаживание (обычно задается в диапазоне от 1e-4 до 1e-8) позволяет избежать деления на ноль. Недостатком Adagrad является то, что в случае глубокого обучения монотонный темп обучения обычно оказывается слишком агрессивным и прекращает обучение слишком рано.cache eps

RMSprop — это очень эффективный, но в настоящее время неопубликованный метод адаптивной скорости обучения. Забавно, что все, кто использует этот метод в своей работе, в настоящее время цитируют слайд 29 лекции 6 курса Джеффа Хинтона на Coursera. Обновление RMSProp очень просто корректирует метод Adagrad в попытке снизить его агрессивную, монотонно снижающуюся скорость обучения. В частности, вместо этого он использует скользящее среднее квадратов градиентов, дающее:

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

Здесь находится гиперпараметр decay_rate, типичные значения которого равны [0.9, 0.99, 0.999]. Обратите внимание, что обновление x+= идентично Adagrad, но переменнаяcache "учетка". Следовательно, RMSProp по-прежнему модулирует скорость обучения каждого веса на основе величин его градиентов, что имеет положительный уравнительный эффект, но в отличие от Adagrad обновления не становятся монотонно меньше.

Адам. Adam — это недавно предложенное обновление, которое немного похоже на RMSProp с импульсом. (Упрощённое) обновление выглядит следующим образом:

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

Обратите внимание, что обновление выглядит точно так же, как обновление RMSProp, за исключением того, что вместо необработанного (и, возможно, зашумленного) вектора градиента dx используется “сглаженная” версия градиента m. Рекомендуемые значения в документе - eps = 1e-8, beta1 = 0,9, beta2 = 0,999. На практике Adam в настоящее время рекомендуется использовать в качестве алгоритма по умолчанию и часто работает немного лучше, чем RMSProp. Однако часто также стоит попробовать SGD+Nesterov Momentum в качестве альтернативы. Полное обновление Adam также включает механизм коррекции смещения, который компенсирует тот факт, что на первых нескольких временных шагах векторы m,v инициализируются и, следовательно, смещаются на ноль, прежде чем они полностью “разогреются”. С механизмом коррекции смещения обновление выглядит следующим образом:

# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt / (np.sqrt(vt) + eps)

Обратите внимание, что обновление теперь является функцией итерации, а также других параметров. Мы отсылаем читателя к статье для получения подробной информации или к слайдам курса, где это подробно рассматривается.

Дополнительные ссылки:

• Модульные тесты для стохастической оптимизации предлагают серию тестов в качестве стандартизированного эталона для стохастической оптимизации.

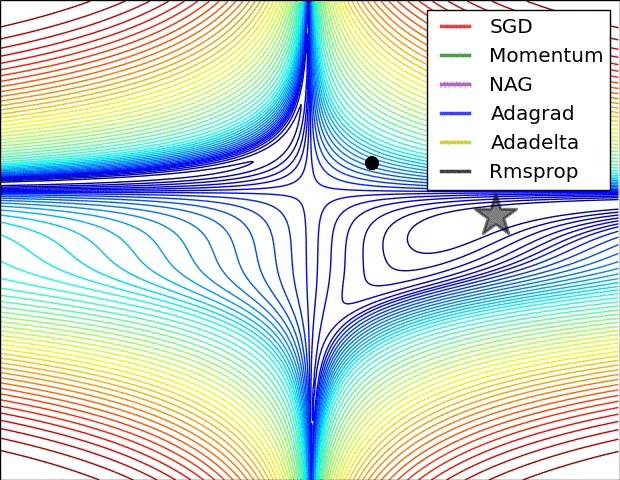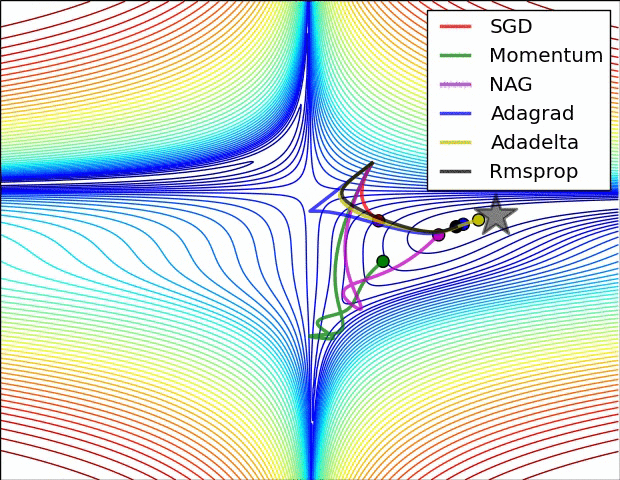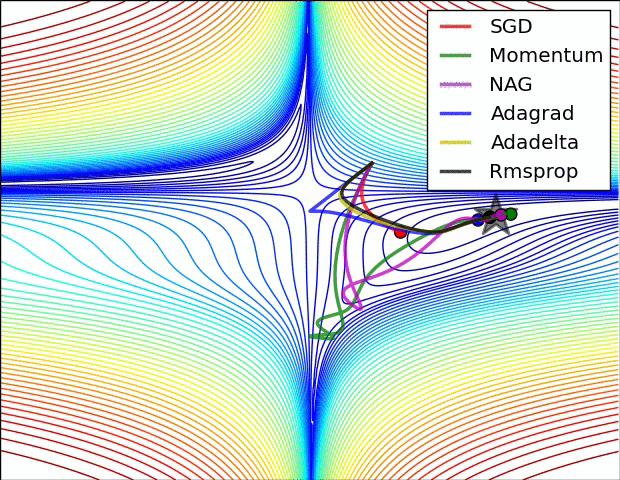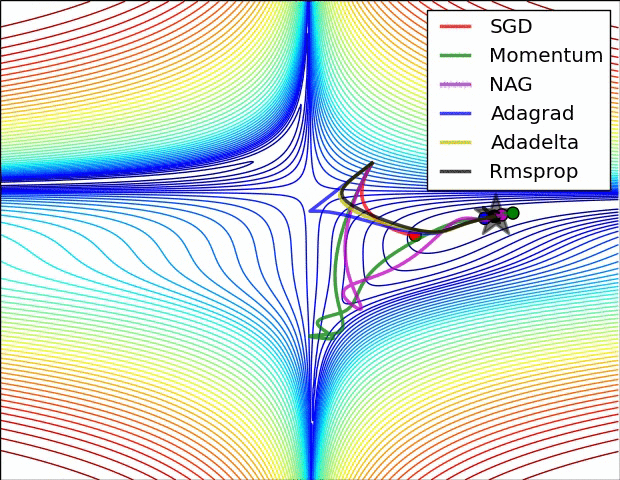
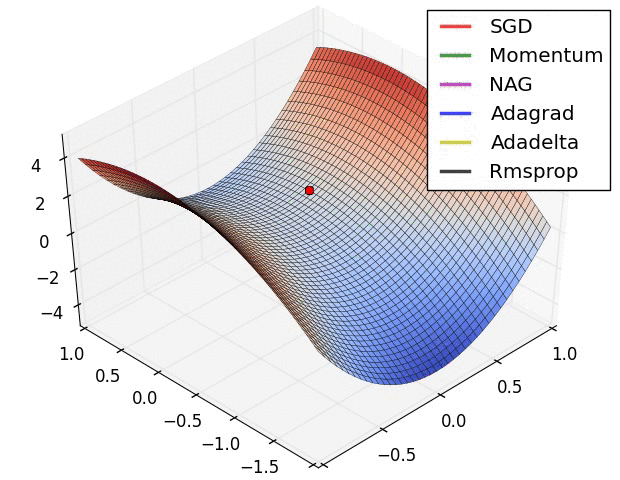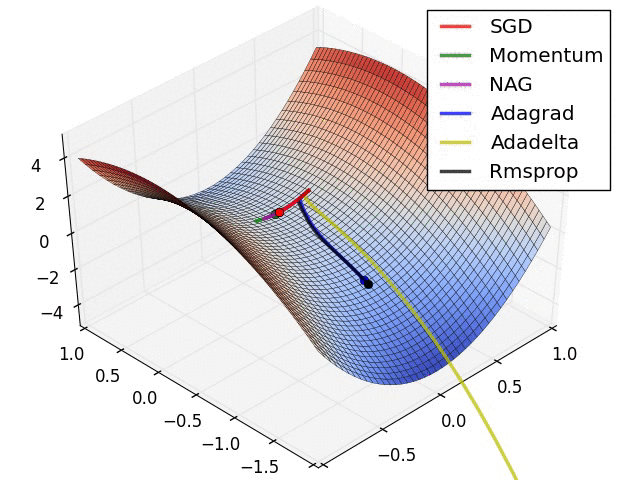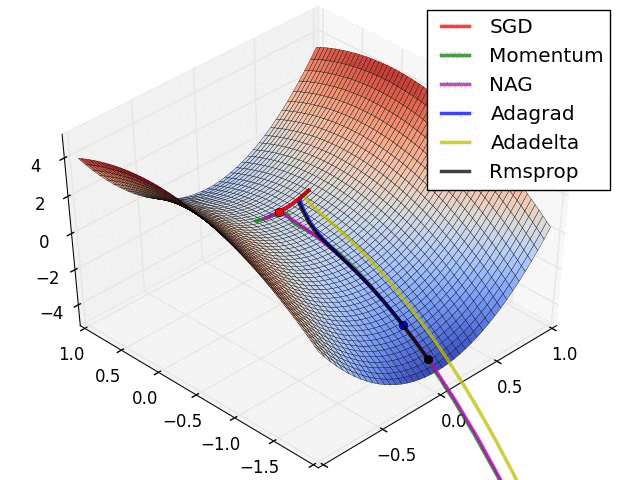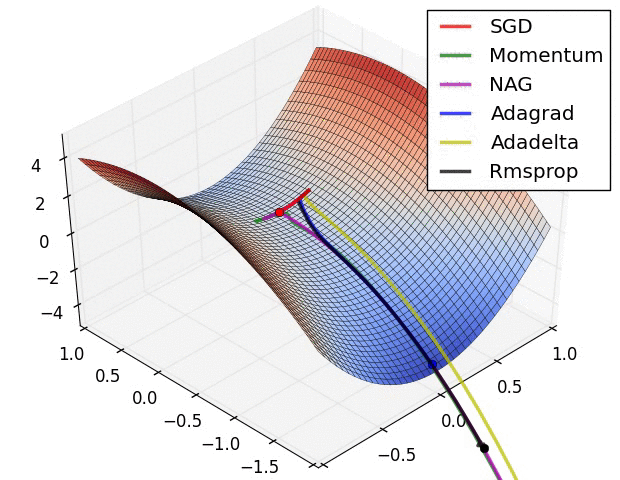
Анимация, которая может помочь вашей интуиции о динамике процесса обучения. Сверху: Контуры поверхности потерь и временная эволюция различных алгоритмов оптимизации. Обратите внимание на «чрезмерное» поведение методов, основанных на импульсе, из-за чего оптимизация выглядит как мяч, катящийся с горки.
Снизу: Визуализация седловой точки в ландшафте оптимизации, где кривизна по разным размерностям имеет разные знаки (одно измерение искривляется вверх, а другое вниз). Обратите внимание, что SGD с трудом нарушает симметрию и застревает на вершине. И наоборот, такие алгоритмы, как RMSprop, будут видеть очень низкие градиенты в направлении седла. Из-за знаменателя в обновлении RMSprop это увеличит эффективную скорость обучения в этом направлении, что поможет RMSProp двигаться дальше. Изображения предоставлены: Алек Рэдфорд.

Оптимизация гиперпараметров

Как мы уже видели, обучение нейронных сетей может включать в себя множество настроек гиперпараметров. К наиболее распространенным гиперпараметрам в контексте нейронных сетей относятся:

• начальная скорость обучения
• График снижения скорости обучения (например, постоянная затухания)
• регуляризация силы (штраф \(L_2\), сила отсева)

Но, как мы видели, относительно менее чувствительных гиперпараметров гораздо больше, например, в попараметрических адаптивных методах обучения, настройке импульса и его расписания и т.д. В этом разделе мы опишем некоторые дополнительные советы и рекомендации по выполнению поиска гиперпараметров:

Реализация. Более крупные нейронные сети обычно требуют много времени для обучения, поэтому выполнение поиска гиперпараметров может занять много дней/недель. Важно помнить об этом, так как это влияет на дизайн вашей кодовой базы. Одна из особенностей проекта заключается в том, чтобы иметь воркер/работника, который постоянно отбирает случайные гиперпараметры и выполняет оптимизацию. Во время обучения сотрудник будет отслеживать производительность проверки после каждой эпохи и записывать контрольную точку модели (вместе с различной статистикой обучения, такой как потери с течением времени) в файл, предпочтительно в общей файловой системе. Полезно указывать производительность проверки непосредственно в имени файла, чтобы было легко проверить и отсортировать ход выполнения. Затем есть вторая программа, которую мы будем называть мастером, которая запускает или убивает рабочих по всему вычислительному кластеру, а также может дополнительно проверять контрольные точки, написанные рабочими, и строить статистику их обучения и т. д.

Отдайте предпочтение одной свертке проверки перекрестной проверке. В большинстве случаев один валидационный набор приличного размера существенно упрощает кодовую базу без необходимости перекрестной валидации с несколькими свертками. Вы можете услышать, как люди говорят, что они «перекрестно проверили» параметр, но часто предполагается, что они все еще использовали только один набор проверки.

Диапазоны гиперпараметров. Поиск гиперпараметров в логарифмической шкале. Например, типичная выборка коэффициента обучения будет выглядеть следующим образом: learning_rate = 10 ** uniform(-6, 1). То есть мы генерируем случайное число из равномерного распределения, но затем возводим его в степень 10. Та же стратегия должна быть использована и для силы регуляризации. Интуитивно это объясняется тем, что скорость обучения и сила регуляризации оказывают мультипликативное влияние на динамику тренировки. Например, фиксированное изменение при добавлении 0,01 к коэффициенту обучения оказывает огромное влияние на динамику, если коэффициент обучения равен 0,001, но почти не оказывает никакого влияния, если коэффициент обучения равен 10. Это связано с тем, что скорость обучения умножает вычисленный градиент в обновлении. Следовательно, гораздо естественнее рассматривать диапазон скорости обучения, умноженный или деленный на некоторую величину, чем диапазон скорости обучения, прибавленный или вычтенный на некоторую величину. Некоторые параметры (например, отсеивание) обычно ищутся в исходной шкале (например, dropout = uniform(0,1)).

Отдайте предпочтение случайному поиску, а не поиску по сетке. Как утверждают Бергстра и Бенджио в книге «Случайный поиск для оптимизации гиперпараметров», «случайно выбранные испытания более эффективны для оптимизации гиперпараметров, чем испытания на сетке» . Как оказалось, это тоже обычно проще реализовать.

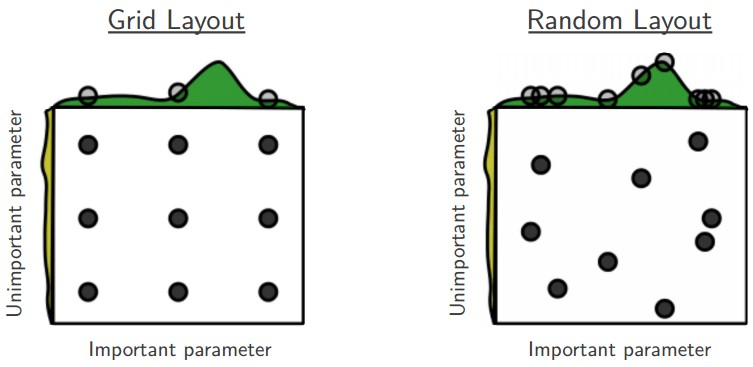
Основная иллюстрация из книги «Случайный поиск для оптимизации гиперпараметров» Бергстры и Бенджио. Очень часто бывает так, что некоторые гиперпараметры имеют гораздо большее значение, чем другие (например, верхний гиперпараметр против левого на этом рисунке). Выполнение случайного поиска, а не поиска по сетке, позволяет гораздо точнее находить хорошие значения для важных.

Осторожнее с лучшими значениями на границе. Иногда может случиться так, что вы ищете гиперпараметр (например, скорость обучения) в плохом диапазоне. Например, предположим, что мы используем learning_rate = 10 ** uniform(-6, 1) . Как только мы получим результаты, важно еще раз проверить, что итоговая скорость обучения не находится на краю этого интервала, иначе вы можете пропустить более оптимальную настройку гиперпараметров за пределами интервала.

Этапируйте свой поиск от грубого к хорошему. На практике может быть полезно сначала искать в грубых диапазонах (например, 10 ** [-6, 1]), а затем, в зависимости от того, где появляются наилучшие результаты, сужать диапазон. Кроме того, может быть полезно выполнить первоначальный грубый поиск во время обучения только за 1 эпоху или даже меньше, потому что многие настройки гиперпараметров могут привести к тому, что модель вообще не будет обучаться или сразу же взорвется с бесконечными затратами. Второй этап может выполнять более узкий поиск с 5 эпохами, а последний этап может выполнять детальный поиск в конечном диапазоне для гораздо большего количества эпох (например).

Байесовская оптимизация гиперпараметров — это целая область исследований, посвященная созданию алгоритмов, которые пытаются более эффективно ориентироваться в пространстве гиперпараметров. Основная идея заключается в том, чтобы правильно сбалансировать компромисс между исследованием и эксплуатацией при запросе производительности при различных гиперпараметрах. На основе этих моделей также было разработано несколько библиотек, среди наиболее известных — Spearmint, SMAC и Hyperopt. Тем не менее, в практических условиях с ConvNet все еще относительно сложно превзойти случайный поиск в тщательно выбранных интервалах. Смотрите дополнительную дискуссию из окопов здесь.

Оценка

Модельные ансамбли

На практике одним из надежных подходов к повышению производительности нейронных сетей на несколько процентов является обучение нескольких независимых моделей и усреднение их прогнозов во время тестирования. По мере увеличения числа моделей в ансамбле производительность обычно монотонно улучшается (хотя и с уменьшением отдачи). Более того, улучшения более значительны с большим разнообразием моделей в ансамбле. Существует несколько подходов к формированию ансамбля:

• Одна и та же модель, разные инициализации. Используйте перекрестную проверку для определения наилучших гиперпараметров, а затем обучите несколько моделей с лучшим набором гиперпараметров, но с разной случайной инициализацией. Опасность при таком подходе заключается в том, что сорт получается только за счет инициализации.
• Лучшие модели, обнаруженные во время перекрестной проверки. Используйте перекрестную проверку для определения наилучших гиперпараметров, а затем выберите несколько лучших (например, 10) моделей для формирования ансамбля. Это повышает разнообразие ансамбля, но чревато опасностью включения неоптимальных моделей. На практике это может быть проще выполнить, так как не требует дополнительного переобучения моделей после перекрестной проверки
• Разные контрольные точки одной модели. Если обучение стоит очень дорого, то некоторые люди имеют ограниченный успех в прохождении различных контрольных точек одной сети с течением времени (например, после каждой эпохи) и использовании их для формирования ансамбля. Очевидно, что это страдает от некоторого недостатка разнообразия, но все же может работать достаточно хорошо на практике. Преимущество такого подхода в том, что он очень дешевый.
• Бегущее среднее по параметрам во время тренировки. Что касается последнего пункта, то дешевый способ почти всегда получить дополнительный процент или два производительности — это хранить в памяти вторую копию весовых коэффициентов сети, которая поддерживает экспоненциально уменьшающуюся сумму предыдущих весов во время обучения. Таким образом, вы усредняете состояние сети за последние несколько итераций. Вы обнаружите, что эта «сглаженная» версия весов за последние несколько шагов почти всегда приводит к лучшей ошибке проверки. Грубая интуиция, которую следует иметь в виду, заключается в том, что цель имеет форму чаши, и ваша сеть прыгает вокруг режима, поэтому среднее значение имеет больше шансов оказаться где-то ближе к режиму.

Одним из недостатков ансамблей моделей является то, что их оценка на тестовом примере занимает больше времени. Заинтересованного читателя может вдохновить недавняя работа Джеффа Хинтона «Темное знание», в которой идея состоит в том, чтобы «дистиллировать» хороший ансамбль обратно к одной модели, включив логарифмические правдоподобия ансамбля в модифицированную цель.

Краткая сводка

Чтобы обучить нейронную сеть:

• Градиент: проверьте свою реализацию с помощью небольшого пакета данных и помните о подводных камнях.
• В качестве проверки здравого смысла убедитесь, что ваши первоначальные потери разумны, и что вы можете достичь 100% точности обучения на очень небольшой части данных
• Во время обучения отслеживайте потери, точность обучения/проверки, а если вы чувствуете себя более склонным, величину обновлений по отношению к значениям параметров (она должна быть ~1e-3), а при работе с ConvNet — веса первого слоя.
• Рекомендуется использовать два обновления: SGD+Nesterov Momentum или Adam.
• Снижайте скорость обучения в течение периода обучения. Например, уменьшите вдвое скорость обучения после фиксированного количества эпох или всякий раз, когда точность проверки достигает максимума.
• Поиск хороших гиперпараметров с помощью случайного поиска (не поиска по сетке). Дифференцируйте поиск от грубого (широкие диапазоны гиперпараметров, обучение только для 1-5 эпох) до тонкого (более узкие рейнджеры, обучение для гораздо большего количества эпох)
• Формируйте модельные ансамбли для дополнительной производительности

Дополнительные материалы

• SGD советы и рекомендации от Леона Ботту
• Efficient BackProp (pdf) от Яна Лекуна
• Практические рекомендации по градиентному обучению глубокого Архитектура от Йошуа Бенджио