Обучение нейронных сетей 2

Обучение нейронных сетей

Содержание: - Генерация некоторых данных - Обучение линейного классификатора Softmax - Инициализируйте параметры - Подсчитайте баллы за класс - Вычислите потери - Вычисление аналитического градиента с обратным распространением - Выполнение обновления параметров - Сведение всего этого воедино: обучение классификатора Softmax - Обучение нейронной сети - Краткая сводка - Дополнительные материалы

В этом разделе мы рассмотрим полную реализацию игрушечной нейронной сети в двух измерениях. Сначала мы реализуем простой линейный классификатор, а затем расширим код до двухслойной нейронной сети. Как мы увидим, это расширение на удивление простое, и требуется внести совсем немного изменений.

Генерация некоторых данных

Давайте создадим набор данных для классификации, который нелегко разделить на линейные классы. Наш любимый пример — набор данных «спираль», который можно создать следующим образом:

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()

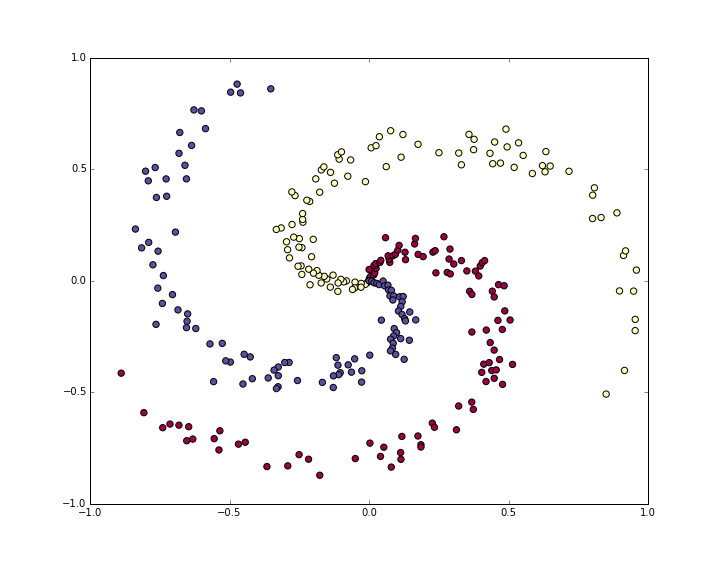
Данные игрушечной спирали состоят из трёх классов (синий, красный, жёлтый), которые нельзя разделить линейно.

Обычно мы хотим предварительно обработать набор данных, чтобы среднее значение каждого признака было равно нулю, а стандартное отклонение — единице, но в данном случае признаки уже находятся в диапазоне от -1 до 1, поэтому мы пропускаем этот шаг.

Обучение линейного классификатора Softmax

Инициализируйте параметры

Давайте сначала обучим классификатор Softmax на этом наборе данных для классификации. Как мы видели в предыдущих разделах, классификатор Softmax имеет линейную функцию оценки и использует функцию потерь кросс-энтропии. Параметры линейного классификатора состоят из весовой матрицы W и вектора смещения b для каждого класса. Давайте сначала инициализируем эти параметры случайными числами:

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

Напомним, что D = 2 — это размерность, а K = 3 — количество классов.

Подсчитайте баллы за класс

Поскольку это линейный классификатор, мы можем очень просто вычислить оценки для всех классов параллельно с помощью одного умножения матриц:

# compute class scores for a linear classifier
scores = np.dot(X, W) + b

В этом примере у нас есть 300 двумерных точек, поэтому после этого умножения массив scores будет иметь размер [300 x 3], где каждая строка содержит баллы за классы, соответствующие трём классам (синий, красный, жёлтый).

Вычислите потери

Второй ключевой компонент, который нам нужен, — это функция потерь, представляющая собой дифференцируемую целевую функцию, которая количественно оценивает наше недовольство вычисленными оценками классов. Интуитивно понятно, что мы хотим, чтобы правильный класс имел более высокую оценку, чем другие классы. В этом случае потери должны быть низкими, а в противном случае — высокими. Существует множество способов количественно оценить эту интуитивную догадку, но в этом примере мы будем использовать потери перекрёстной энтропии, которые связаны с классификатором Softmax. Напомним, что если f — это массив оценок классов для одного примера (например, массив из трёх чисел), тогда классификатор Softmax вычисляет потерю для этого примера следующим образом:

$$ L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) $$

Мы можем видеть, что классификатор Softmax интерпретирует каждый элемент f. В качестве входных данных используются (ненормализованные) логарифмические вероятности трёх классов. Мы возводим их в степень, чтобы получить (ненормализованные) вероятности, а затем нормализуем их, чтобы получить вероятности. Таким образом, выражение внутри логарифма — это нормализованная вероятность правильного класса. Обратите внимание на то, как работает это выражение: эта величина всегда находится в диапазоне от 0 до 1. Когда вероятность правильного класса очень мала (близка к 0), потери будут стремиться к (положительной) бесконечности. И наоборот, когда вероятность правильного класса приближается к 1, потери приближаются к нулю, потому что log(1)=0. Следовательно, выражение для \(L_i\). Вероятность правильного класса низкая, когда она высока, и очень высокая, когда она низка.

Напомним также, что полная потеря классификатора Softmax определяется как средняя потеря кросс-энтропии по обучающим примерам и регуляризация:

$$ L = \underbrace{ \frac{1}{N} \sum_i L_i }\text{потеря данных} + \underbrace{ \frac{1}{2} \lambda \sum_k\sum_l W \\ $$ }^2 }_\text{потеря регуляризации

Учитывая массив scores значений, которые мы вычислили выше, мы можем вычислить потери. Во-первых, способ получения вероятностей прост:

num_examples = X.shape[0]
# get unnormalized probabilities
exp_scores = np.exp(scores)
# normalize them for each example
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

Теперь у нас есть массив probs размером [300 x 3], где каждая строка содержит вероятности классов. В частности, поскольку мы их нормализовали, сумма значений в каждой строке равна единице. Теперь мы можем запросить логарифмические вероятности, присвоенные правильным классам в каждом примере:

orrect_logprobs = -np.log(probs[range(num_examples),y])

Массив correct_logprobs — это одномерный массив, содержащий только вероятности, присвоенные правильным классам для каждого примера. Полная потеря — это среднее значение этих логарифмических вероятностей и потери от регуляризации:

# compute the loss: average cross-entropy loss and regularization
data_loss = np.sum(correct_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss

В этом коде сила регуляризации λ хранится внутри reg. Коэффициент удобства 0.5 умножения регуляризации станет ясен через секунду. Оценка этого вначале (со случайными параметрами) может дать нам loss = 1.1, что и есть -np.log(1.0/3), поскольку при небольших начальных случайных весах все вероятности, присвоенные всем классам, составляют около одной трети. Теперь мы хотим сделать потери как можно более низкими, используя loss = 0 в качестве абсолютной нижней границы. Но чем меньше потери, тем выше вероятности, присвоенные правильным классам для всех примеров.

Вычисление аналитического градиента с обратным распространением

У нас есть способ оценки потерь, и теперь нам нужно их минимизировать. Мы сделаем это с помощью градиентного спуска. То есть мы начнём со случайных параметров (как показано выше) и вычислим градиент функции потерь по отношению к параметрам, чтобы знать, как изменить параметры для уменьшения потерь. Давайте введём промежуточную переменную p, который представляет собой вектор (нормализованных) вероятностей. Потери для одного примера составляют:

$$ p_k = \frac{e^{f_k}}{ \sum_j e^{f_j} } \hspace{1in} L_i =-\log\left(p_{y_i}\right) $$

Теперь мы хотим понять, как вычисляются баллы внутри f следует изменить, чтобы уменьшить потери \(L_i\), что этот пример соответствует общей цели. Другими словами, мы хотим вычислить градиент \( \partial L_i / \partial f_k \). Потеря __\(L_i\)__вычисляется из p, что , в свою очередь , зависит от f. Читателю будет интересно использовать правило дифференцирования сложной функции для вычисления градиента, но в итоге всё оказывается очень простым и понятным, после того как многое сокращается:

$$ \frac{\partial L_i }{ \partial f_k } = p_k - \mathbb{1}(y_i = k) $$

Обратите внимание, насколько элегантно и просто выглядит это выражение. Предположим, что вычисленные нами вероятности были p = [0.2, 0.3, 0.5] и что правильным классом был средний (с вероятностью 0,3). Согласно этому выводу, градиент оценок будет равен df = [0.2, -0.7, 0.5]. Вспомнив, что означает интерпретация градиента, мы видим, что этот результат вполне интуитивен: увеличение первого или последнего элемента вектора оценок f (оценок неверных классов) приводит к увеличению потерь (из-за положительных значений +0,2 и +0,5) — а увеличение потерь плохо, как и ожидалось. Однако увеличение оценки правильного класса отрицательно влияет на потери. Градиент -0,7 говорит нам о том, что увеличение оценки правильного класса приведёт к уменьшению потерь \(L_i\), что имеет смысл.

Всё это сводится к следующему коду. Напомним, что probs хранит вероятности всех классов (в виде строк) для каждого примера. Чтобы получить градиент оценок, который мы называем dscores, мы поступаем следующим образом:

dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

Наконец, у нас есть scores = np.dot(X, W) + b и, вооружившись градиентом scores (хранящимся в dscores), мы можем выполнить обратное распространение ошибки в W и b:

dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient

Здесь мы видим, что мы выполнили обратное преобразование с помощью операции умножения матриц, а также добавили вклад от регуляризации. Обратите внимание, что градиент регуляризации имеет очень простую форму reg*W, поскольку мы использовали константу 0.5 для вклада в потери (т. е. \(\frac{d}{dw} ( \frac{1}{2} \lambda w^2) = \lambda w\) ). Это распространенный удобный прием, который упрощает выражение градиента.

Выполнение обновления параметров

Теперь, когда мы вычислили градиент, мы знаем, как каждый параметр влияет на функцию потерь. Теперь мы обновим параметры в направлении отрицательного градиента, чтобы уменьшить потери:

# perform a parameter update
W += -step_size * dW
b += -step_size * db

Сведение всего этого воедино: обучение классификатора Softmax

Если собрать всё это воедино, получится полный код для обучения классификатора Softmax с помощью градиентного спуска:

#Train a Linear Classifier

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(200):

  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b

  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]

  # compute the loss: average cross-entropy loss and regularization
  correct_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(correct_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print "iteration %d: loss %f" % (i, loss)

  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples

  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)

  dW += reg*W # regularization gradient

  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db
  ```


 При выполнении этой операции выводятся выходные данные:  

 ```
 iteration 0: loss 1.096956
iteration 10: loss 0.917265
iteration 20: loss 0.851503
iteration 30: loss 0.822336
iteration 40: loss 0.807586
iteration 50: loss 0.799448
iteration 60: loss 0.794681
iteration 70: loss 0.791764
iteration 80: loss 0.789920
iteration 90: loss 0.788726
iteration 100: loss 0.787938
iteration 110: loss 0.787409
iteration 120: loss 0.787049
iteration 130: loss 0.786803
iteration 140: loss 0.786633
iteration 150: loss 0.786514
iteration 160: loss 0.786431
iteration 170: loss 0.786373
iteration 180: loss 0.786331
iteration 190: loss 0.786302

Мы видим, что после примерно 190 итераций мы приблизились к чему-то. Мы можем оценить точность обучающего набора данных:

# evaluate training set accuracy
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

Это выводит 49%. Не очень хорошо, но и неудивительно, учитывая, что набор данных составлен таким образом, что он не является линейно разделимым. Мы также можем построить границы принятых решений:

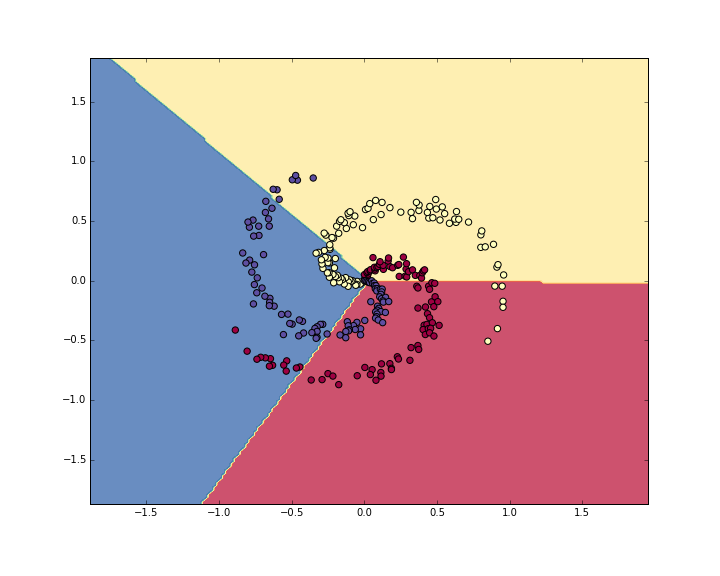
Линейный классификатор не может изучить набор данных toy spiral.

Обучение нейронной сети

Очевидно, что линейный классификатор не подходит для этого набора данных, и мы хотели бы использовать нейронную сеть. Для этих игрушечных данных будет достаточно одного дополнительного скрытого слоя. Теперь нам понадобятся два набора весовых коэффициентов и смещений (для первого и второго слоев):

# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))

Прямой проход для подсчета очков теперь меняет форму:

# evaluate class scores with a 2-layer Neural Network
hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation
scores = np.dot(hidden_layer, W2) + b2

Обратите внимание, что единственное отличие от предыдущего варианта — это одна дополнительная строка кода, в которой мы сначала вычисляем представление скрытого слоя, а затем баллы на основе этого скрытого слоя. Важно отметить, что мы также добавили нелинейность, которая в данном случае представляет собой простую функцию ReLU, устанавливающую пороговое значение активации скрытого слоя на нуле.

Всё остальное остаётся прежним. Мы вычисляем потери на основе оценок точно так же, как и раньше, и получаем градиент для оценок dscores точно так же, как и раньше. Однако способ обратного распространения этого градиента на параметры модели, конечно, меняется. Сначала давайте выполним обратное распространение для второго слоя нейронной сети. Это выглядит так же, как и код для классификатора Softmax, за исключением того, что мы заменяем X (исходные данные) на переменную hidden_layer):

```# backpropate the gradient to the parameters

first backprop into parameters W2 and b2

dW2 = np.dot(hidden_layer.T, dscores) db2 = np.sum(dscores, axis=0, keepdims=True)

Однако, в отличие от предыдущего случая, мы ещё не закончили, потому что `hidden_layer` сама является функцией других параметров и данных! Нам нужно продолжить обратное распространение ошибки через эту переменную. Её градиент можно вычислить следующим образом:  

dhidden = np.dot(dscores, W2.T)

Теперь у нас есть градиент на выходе скрытого слоя. Далее нам нужно выполнить обратное распространение ошибки для нелинейности **ReLU**. Это оказывается простым, потому что **ReLU** при обратном распространении ошибки фактически является переключателем. Поскольку **r=max(0,x)**, у нас есть это **dr/dx=1(x>0)**. В сочетании с правилом дифференцирования по частям мы видим, что блок **ReLU** пропускает градиент без изменений, если его входные данные больше 0, но _отменяет_ его, если входные данные меньше нуля во время прямого прохода. Следовательно, мы можем выполнить обратное распространение ошибки для **ReLU** следующим образом:  

backprop the ReLU non-linearity

dhidden[hidden_layer <= 0] = 0

И теперь мы, наконец, переходим к первому слою весов и смещений:  

finally into W,b

dW = np.dot(X.T, dhidden) db = np.sum(dhidden, axis=0, keepdims=True)

**Готово!** У нас есть градиенты `dW,db,dW2,db2` и мы можем выполнить обновление параметров. Всё остальное остаётся без изменений. Полный код выглядит очень похоже:  

initialize parameters randomly

h = 100 # size of hidden layer W = 0.01 * np.random.randn(D,h) b = np.zeros((1,h)) W2 = 0.01 * np.random.randn(h,K) b2 = np.zeros((1,K))

some hyperparameters

step_size = 1e-0 reg = 1e-3 # regularization strength

gradient descent loop

num_examples = X.shape[0] for i in range(10000):

# evaluate class scores, [N x K] hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation scores = np.dot(hidden_layer, W2) + b2

# compute the class probabilities exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]

# compute the loss: average cross-entropy loss and regularization correct_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(correct_logprobs)/num_examples reg_loss = 0.5regnp.sum(WW) + 0.5regnp.sum(W2W2) loss = data_loss + reg_loss if i % 1000 == 0: print "iteration %d: loss %f" % (i, loss)

# compute the gradient on scores dscores = probs dscores[range(num_examples),y] -= 1 dscores /= num_examples

# backpropate the gradient to the parameters # first backprop into parameters W2 and b2 dW2 = np.dot(hidden_layer.T, dscores) db2 = np.sum(dscores, axis=0, keepdims=True) # next backprop into hidden layer dhidden = np.dot(dscores, W2.T) # backprop the ReLU non-linearity dhidden[hidden_layer <= 0] = 0 # finally into W,b dW = np.dot(X.T, dhidden) db = np.sum(dhidden, axis=0, keepdims=True)

# add regularization gradient contribution dW2 += reg * W2 dW += reg * W

# perform a parameter update W += -step_size * dW b += -step_size * db W2 += -step_size * dW2 b2 += -step_size * db2 ```

Это печатает:

iteration 0: loss 1.098744
iteration 1000: loss 0.294946
iteration 2000: loss 0.259301
iteration 3000: loss 0.248310
iteration 4000: loss 0.246170
iteration 5000: loss 0.245649
iteration 6000: loss 0.245491
iteration 7000: loss 0.245400
iteration 8000: loss 0.245335
iteration 9000: loss 0.245292

Точность обучения теперь равна:

# evaluate training set accuracy
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

Что выводит 98%!. Мы также можем визуализировать границы решений:

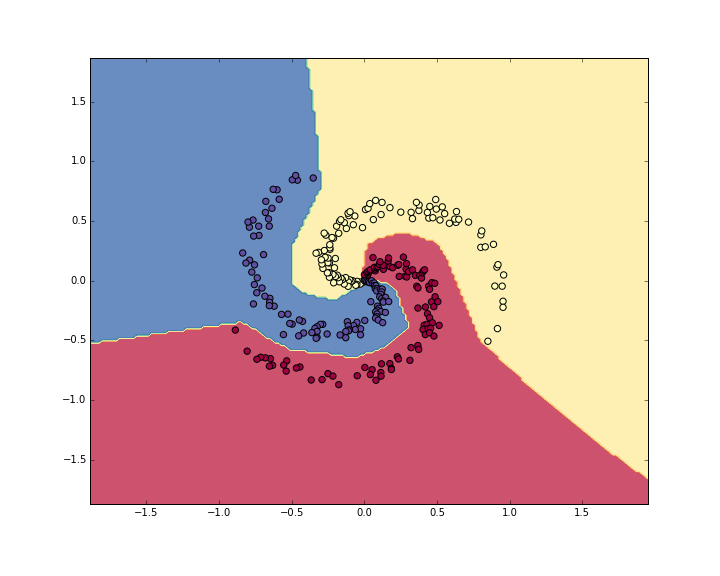
Классификатор нейронной сети сжимает набор данных spiral.

Краткие сведения

Мы работали с игрушечным 2D-набором данных и обучали как линейную сеть, так и двухслойную нейронную сеть. Мы увидели, что переход от линейного классификатора к нейронной сети требует очень мало изменений в коде. Функция оценки меняет свою форму (разница в 1 строке кода), а обратное распространение ошибки меняет свою форму (нам нужно выполнить ещё один цикл обратного распространения ошибки через скрытый слой к первому слою сети).

Дополнительные материалы

• Возможно, вам захочется взглянуть на этот код IPython Notebook отображаемый в формате HTML.
• Или загрузите файл ipynb