Эпиполярная геометрия

Введение

В предыдущих разделах мы изучали методы расчёта внутренних и внешних параметров камеры. Это можно сделать с помощью стандартной процедуры калибровки камеры или используя знания о перпендикулярных плоскостях по одному изображению. В результате этих вычислений мы смогли получить определённые характеристики трёхмерного пространства.

Однако в общем случае невозможно восстановить полную структуру трёхмерного мира, опираясь только на одно изображение. Причина этого кроется во внутренней неоднозначности процесса отображения трёхмерного пространства на двумерную плоскость — часть информации неизбежно теряется при таком преобразовании.

Рисунок 1: Проблема неоднозначности

Рассмотрим характерный пример, показанный на рисунке 1. На первый взгляд может показаться, что человек действительно удерживает Пизанскую башню. Только при внимательном изучении изображения становится понятно, что это всего лишь оптическая иллюзия, возникшая из-за проецирования объектов с разной глубиной на плоскость изображения.

Если же рассмотреть эту сцену с совершенно другой точки зрения, иллюзия исчезает, и мы можем определить правильное расположение объектов в пространстве. Именно поэтому использование нескольких точек обзора является ключевым для точного понимания структуры сцены.

1. Эпиполярная геометрия

Эпиполярная геометрия представляет собой раздел компьютерной геометрии, который изучает взаимосвязь между точками на разных изображениях, ограничения на их расположение при проецировании и геометрические соотношения между камерами.

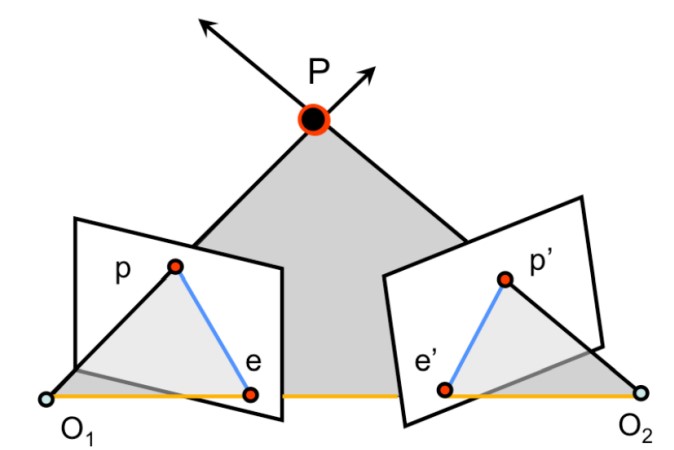
Рисунок 2: Основные элементы эпиполярной геометрии

Рассмотрим основные элементы эпиполярной геометрии, изображённые на рисунке 2:

• Две камеры наблюдают одну и ту же трёхмерную точку $P$
• Проекции точки $P$ на плоскости изображений находятся в точках $p$ и $p'$
• Центры камер расположены в точках $O_1$ и $O_2$
• Линия, соединяющая центры камер, называется базисом (оранжевая линия)
• Плоскость, образованная двумя центрами камер и точкой $P$, называется эпиполярной плоскостью (изображена серым цветом)
• Эпиполы — точки пересечения базиса с плоскостями изображений ($e$ и $e'$)
• Эпиполярные линии — прямые, образованные пересечением эпиполярной плоскости с плоскостями изображений (голубые отрезки)

Рисунок 3: Пример расположения эпиполярных линий и ключевых точек

На рисунке 3 показан пример эпиполярных линий и соответствующих ключевых точек, нанесённых на пару изображений. Эта визуализация демонстрирует, как эпиполярная геометрия помогает установить связь между точками на разных снимках.

Таким образом, эпиполярная геометрия помогает установить связи между изображениями одной и той же сцены, снятыми с разных точек зрения, и восстанавливать трёхмерную структуру.

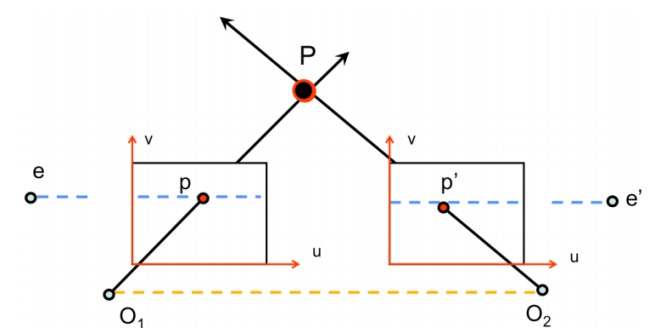
Рисунок 4: Частный случай эпиполярной геометрии

Рассмотрим интересную ситуацию, когда плоскости изображений расположены параллельны друг другу (см. рисунок 4). В этом случае эпиполы $e$ и $e'$ располагаются в бесконечности. Это происходит потому, что базис, соединяющий центры камер $O_1$ и $O_2$, параллелен плоскостям изображений. Эпиполярные линии становятся параллельными оси $u$ на плоскости изображения.

Этот частный случай имеет важное практическое значение, особенно при работе с выравниванием изображений, о чём будет подробно рассказано в следующем разделе.

В практических ситуациях точное расположение трёхмерной точки $P$ неизвестно. Но мы можем определить её проекции $p, p'$ на плоскости изображений, местоположение, ориентацию и внутренние параметры камер.

Кроме того, зная положения камер $O_1$, $O_2$ и положение проекции точки $p$ на одном изображении, можно определить эпиполярную плоскость и найти эпиполярные линии на основе этой плоскости. Это существенно упрощает поиск соответствующей ключевой точки на других изображениях. Это свойство делает эпиполярную геометрию мощным инструментом в задачах компьютерного зрения и трёхмерной реконструкции сцены.

2. Эссенциальная матрица

Для создания эффективного способа отображения точек и эпиполярных линий между разными видами сцены мы используем базовую структуру эпиполярной геометрии. В этой системе матрицы проекции $M$ и $M'$ отвечают за преобразование трёхмерных точек в двумерные координаты на плоскостях изображений. Мировая система координат связывается с первой камерой, при этом вторая камера смещается относительно первой через последовательное применение поворота $R$ и переноса $T$.

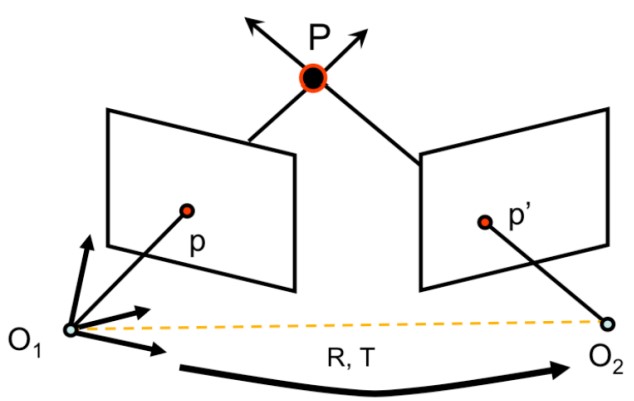
Рисунок 5: Расположение второй камеры относительно первой

В результате того, что за точку отсчета мировых координат мы принимаем центр камеры $O_1$, матрицы проекции принимают следующий вид:

$M = K \begin{bmatrix} I & 0 \end{bmatrix}$ (2)

$M' = K' \begin{bmatrix} R & -RT \end{bmatrix}$

где $K$ и $K'$ представляют внутренние параметры камер, $I$ — единичная матрица, $R$ отвечает за поворот, а $T$ — за перенос (вектор $O_1 O_2$).

Рассмотрим частный случай с каноническими камерами:

$K = K' = I$

$p'$ - это координаты проекции точки в системе координат второй камеры. Координаты точки $p'$ в системе координат первой камеры определяются как $Rp' + T$.

Поскольку векторы $Rp' + T$ и $T$ лежат в эпиполярной плоскости, их векторное произведение даёт вектор, перпендикулярный этой плоскости.
Благодаря свойствам дистрибутивности векторного произведения получаем результат:

$T \times (Rp' + T) = T \times (Rp')$

Точка $p$, лежащая в эпиполярной плоскости, ортогональна вектору $T \times (Rp')$, что даёт ограничение:

$p^T \cdot [T \times (Rp')] = 0$ (3)

Напомним, векторное произведение — это операция над двумя векторами в трёхмерном пространстве, результатом которой является новый вектор. Результат — вектор, перпендикулярный обоим исходным векторам, его длина равна площади параллелограмма, построенного на исходных векторах, а направление определяется правилом правой руки

Пусть даны два вектора:

$\vec{a} = (a_1, a_2, a_3)$

$\vec{b} = (b_1, b_2, b_3)$

Их векторное произведение:

$\vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$

где $\vec{i}, \vec{j}, \vec{k}$ — единичные векторы по осям координат.

Формула для вычисления имеет вид:

$\vec{a} \times \vec{b} = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1)$

Вернемся к эпиполярной геометрии.

Используя аппарат линейной алгебры, векторное произведение можно представить в виде матрично-векторного умножения:

$a \times b = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = [a\times]b$ (4)

Преобразуя выражение с учётом этого представления, получаем:

$p^T[T\times]Rp' = 0$ (5)

Матрица $E = [T\times]R$ называется эссенциальной матрицей и даёт компактную форму эпиполярного ограничения:

$p^TEp' = 0$ (6)

Эссенциальная матрица — это матрица размером $3 \times 3$, содержащая 5 степеней свободы. Она имеет ранг 2 и является сингулярной.

Эта матрица полезна для вычисления эпиполярных линий. Например, $l' = E^Tp$ даёт эпиполярную линию в плоскости изображения второй камеры, а $l = Ep'$ — в плоскости первой камеры.

Важные свойства эссенциальной матрицы: * Её скалярное произведение с эпиполями равно нулю: $E^Te = Ee' = 0$ * Для любой точки $x$ (кроме $e$) в изображении первой камеры соответствующая эпиполярная линия во второй камере содержит эпиполь $e'$

Таким образом, эссенциальная матрица является фундаментальным инструментом для работы с эпиполярной геометрией и установления связей между точками на разных изображениях.

3. Фундаментальная матрица

Фундаментальная матрица — это важный инструмент в эпиполярной геометрии, который обобщает концепцию эссенциальной матрицы на случай камер с нетривиальными внутренними параметрами.

Рассмотрим матрицы проекции для двух камер:

$M = K \begin{bmatrix} I & 0 \end{bmatrix}$

$M' = K' \begin{bmatrix} R & -RT \end{bmatrix}$ (7)

Для работы с неканоническими камерами введём обозначения: * $p_c = K^{-1}p$ — проекция точки $p$ для канонической камеры * $p'_c = K'^{-1}p'$ — проекция точки $p'$ для канонической камеры

В каноническом случае (единичная матрица $K$) выполняется соотношение:

$p_c^T [T \times] R p'_c = 0$ (8)

Однако, с учетом преобразований внутренних параметров камеры, получаем:

$p^T K^{-T} [T \times] R K'^{-1} p' = 0$ (9)

Матрица $F = K'^{-T} [T \times] R K^{-1}$ называется фундаментальной матрицей.
Она обобщает свойства эссенциальной матрицы, учитывает параметры камер $K$ и $K'$ и содержит информацию о взаимном положении камер. (вращение $R$ и перенос $T$). очками на разных изображениях Фундаментальная матрица имеет 7 степеней свободы (против 5 у эссенциальной матрицы), позволяет находить эпиполярные линии без знания 3D-координат точек и работает даже при неизвестных параметрах камер.

Таким образом, фундаментальная матрица даёт мощный инструмент для установления связей между точками на разных изображениях, не требуя полной информации о параметрах камер или трёхмерных координатах точек.

4. Алгоритм восьми точек для вычисления фундаментальной матрицы

Алгоритм восьми точек — это метод оценки фундаментальной матрицы по двум изображениям сцены без знания параметров камер. Метод был предложен Лонге-Хиггинсом в 1981 году и расширен Хартли в 1995 году.

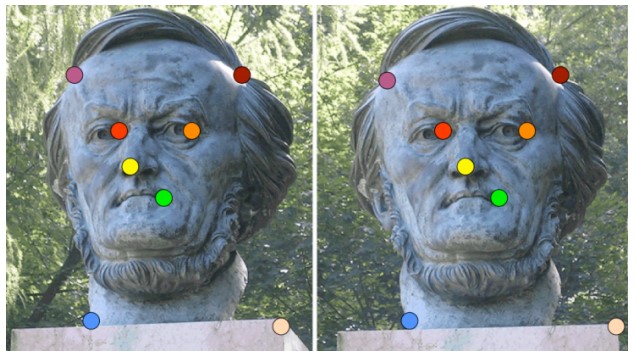
Рисунок 6: Ключевые точки и их соответствие на двух изображениях

Для работы алгоритма требуется минимум 8 пар соответствующих точек между двумя изображениями. Каждая пара точек $p_i = (u_i, v_i, 1)$ и $p'_i = (u'_i, v'_i, 1)$ даёт ограничение $p_i^TFp'_i = 0$.

Математически ограничение можно представить в виде:

$\begin{bmatrix} u_iu'i & v'_iu_i & u_iu'_i & v_iu'_i & v_iv'_i & v_iu'_i & v'_i & 1 \end{bmatrix} \begin{bmatrix} F \end{bmatrix} = 0$} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33

Практическая реализация для $N ≥ 8$ соответствий формируется система уравнений:

$Wf = 0$,

где: * $W$ — матрица размером $N × 9$ * $f$ — вектор элементов фундаментальной матрицы

На практике эффективнее использовать больше восьми соответствий и создавать более крупную матрицу W, поскольку это снижает влияние зашумлённых измерений.

Решение этой системы однородных уравнений можно найти методом наименьших квадратов с помощью сингулярного разложения (SVD), так как матрица W является дефектной по рангу.

SVD даёт оценку фундаментальной матрицы $\hat{F}$, которая может иметь полный ранг. Однако истинная фундаментальная матрица имеет ранг 2, поэтому нужно искать решение, которое является наилучшим приближением ранга 2 для $\hat{F}$.

Математически это формулируется как задача оптимизации:

$\min_F ||F - \hat{F}||_F$ при условии $\det(F) = 0$

где: * $||\cdot||_F$ — норма Фробениуса * $\det(F) = 0$ — условие, обеспечивающее ранг матрицы равный 2

Напомним, сингулярное разложение (SVD) для приблизительной оценки матрицы имеет вид:

$\hat{F} = U\Sigma V^T$

Искомая матрица $F$ будет иметь наилучшее приближение 2 ранга:

$F = U \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & 0 \end{bmatrix} V^T$

где $\sigma_1$ и $\sigma_2$ — первые два сингулярных числа матрицы $\hat{F}$.

Такой подход гарантирует схранение геометрических свойств фундаментальной матрицы, минимизацию отклонения от исходной оценки и сохранение ранга 2.

Таким образом, алгоритм позволяет оценить фундаментальную матрицу без знания параметров камер и является основой для многих задач стереовидения и трёхмерной реконструкции.

5. Нормализованный алгоритм восьми точек

Стандартная реализация алгоритма восьми точек часто даёт неточные результаты. Обычное расстояние между точкой $p_i$ и соответствующей эпиполярной линией $l_i = Fp'_i$ может достигать 10 и более пикселей.

Основная проблема заключается в том, что матрица $W$ плохо обусловлена, это создает проблемы для алгоритма SVD. Основная причина - большие абсолютные значения координат точек (например, $p_i = (1832, 1023, 1)$) Проблема усугубляется, если точки $p_i$ и $p'_i$ находятся в небольшой области изображения, при наличии одного большого сингулярного значения при малых остальных.

Для решения этой проблемы и улучшения точности используется нормализация координат. 1. Сдвиг координат так, чтобы начало новой системы находилось в центре масс точек 2. Масштабирование координат так, чтобы среднеквадратичное расстояние от начала координат равнялось 2 пикселям

Для реализации используются матрицы преобразования $T$ и $T'$, которые выполняют сдвиг на центроид и применяют масштабирующий коэффициент $\left(\frac{2N}{\sum_{i=1}^N||x_i - \bar{x}||^2}\right)^{1/2}$

Нормализованные координаты вычисляются как:
$q_i = Tp_i$
$q'_i = T'p'_i$

Далее, используя нормализованные координаты, вычисляется матрица $F_q$ стандартным методом и производится денормализация:

$F = T'^TF_qT$

Нормализованный алгоритм обеспечивает:
- Более точные результаты в реальных приложениях
- Улучшенную обусловленность матрицы $W$
- Снижение влияния больших значений координат
- Повышение точности оценки фундаментальной матрицы

Такой подход значительно улучшает качество оценки фундаментальной матрицы и является предпочтительным методом для практического применения.

6. Выравнивание изображений (Image Rectification)

Особое свойство эпиполярной геометрии проявляется, когда два изображения параллельны друг другу. Рассмотрим частный случай параллельных плоскостей изображений.

Камеры имеют одинаковую матрицу $K$, отсутствует относительное вращение ($R = I$) и есть только перенос вдоль оси $x$ ($T = (T_x, 0, 0)$)

В этом случае эссенциальная матрица принимает вид:

$E = [T×]R = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \end{bmatrix}$ (17)

Направление эпиполярной линии для точки $p' = (u', v', 1)$ вычисляется как:

$l = Ep' = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \end{bmatrix} \begin{bmatrix} u' \\ v' \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ -T_x \\ T_xv' \end{bmatrix}$ (18)

В этом случае направление эпиполярной линии $l$ горизонтально. Аналогично, направление $l'$ также горизонтально, а все эпиполярные линии параллельны друг другу.
Такое выравнивание изображений позволяет значительно упростить поиск соответствий между точками и упрощает стереообработку и трёхмерную реконструкцию сцены.

Рисунок 7: Ректификация (выравнивание) изображений

Если мы используем эпиполярное ограничение $p^T E p' = 0$, то приходим к тому, что $v = v'$. Это показывает, что точки $p$ и $p'$ имеют одинаковую координату $v$.

Следовательно, между соответствующими точками существует очень простая взаимосвязь. Поэтому выравнивание (процесс приведения любых двух заданных изображений к параллельному виду) становится полезным при определении взаимосвязей между соответствующими точками на изображениях.

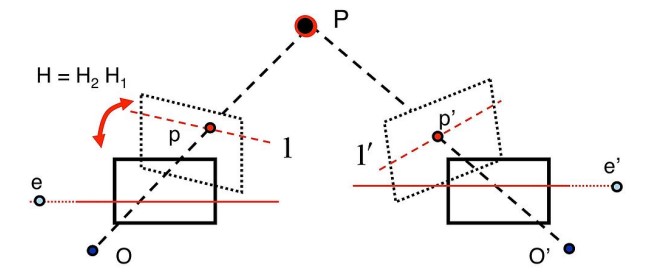
Рисунок 8: Вычисление гомографий ректификации

Выравнивание пары изображений не требует знания матриц камер $K$ и $K'$ или относительного преобразования $R$, $T$ между ними. Вместо этого можно использовать фундаментальную матрицу, оценённую с помощью нормализованного алгоритма восьми точек.

После получения фундаментальной матрицы можно вычислить эпиполярные линии $l_i$ и $l'_i$ для каждой пары соответствующих точек $p_i$ и $p'_i$.

На основе набора эпиполярных линий можно оценить эпиполи $e$ и $e'$ для каждого изображения. Это возможно потому, что эпиполь лежит в точке пересечения всех эпиполярных линий.

В реальных условиях из-за зашумлённых измерений все эпиполярные линии не пересекаются в одной точке. Поэтому вычисление эпиполя можно найти путём минимизации среднеквадратичной ошибки подгонки точки ко всем эпиполярным линиям.

Каждая эпиполярная линия может быть представлена в виде вектора $l$ так, что все точки на линии (в однородных координатах) принадлежат множеству ${x | l^T x = 0}$. Если определить каждую эпиполярную линию как $l_i = [l_{i,1}, l_{i,2}, l_{i,3}]^T$, то можно сформулировать линейную систему уравнений и решить её с помощью сингулярного разложения (SVD) для нахождения эпиполя $e$.

$\begin{bmatrix} l^T_1 \\ \vdots \\ l^T_n \end{bmatrix} e = 0$

После нахождения эпиполей $e$ и $e'$, мы, скорее всего, обнаружим, что они не являются точками на бесконечности вдоль горизонтальной оси. Если бы это было так, то изображения уже были бы параллельными по определению.

Это наводит на мысль: можно ли найти гомографию, которая отобразит эпиполь $e$ в бесконечность вдоль горизонтальной оси?

Все что нам нужно - это найти пару гомографий $H_1$ и $H_2$, применить их к изображениям и отобразить эпиполи в бесконечность.

Начнём с поиска гомографии $H_2$, которая отображает второй эпиполь $e'$ в точку на горизонтальной оси в бесконечности $(f, 0, 0)$.

Хотя существует множество вариантов такой гомографии, на практике хорошо работает условие, при котором гомография действует как преобразование и применяет перенос и поворот к точкам около центра изображения.

Первый шаг — сдвиг второго изображения так, чтобы его центр оказался в точке $(0, 0, 1)$ в однородных координатах. Это достигается применением матрицы переноса.

$T = \begin{bmatrix} 1 & 0 & -\frac{width}{2} \\ 0 & 1 & -\frac{height}{2} \\ 0 & 0 & 1 \end{bmatrix}$ (20)

После применения переноса мы выполняем поворот, чтобы разместить эпиполь на горизонтальной оси в некоторой точке $(f, 0, 1)$.

Если перенесённый эпиполь $T e'$ находится в однородных координатах $(e'_1, e'_2, 1)$, то применяемый поворот определяется следующим образом:

$R = \begin{bmatrix} \alpha\frac{e'_1}{\sqrt{e'^2_1 + e'^2_2}} & \alpha\frac{e'_2}{\sqrt{e'^2_1 + e'^2_2}} & 0 \\ -\alpha\frac{e'_2}{\sqrt{e'^2_1 + e'^2_2}} & \alpha\frac{e'_1}{\sqrt{e'^2_1 + e'^2_2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}$ (21)

где параметр $\alpha$ определяется следующим образом:
$\alpha = 1$, если $e'_1 \geq 0$
$\alpha = -1$ в противном случае.

После применения этого поворота заметим, что для любой точки $(f, 0, 1)$ перевод её в точку на бесконечности по горизонтальной оси $(f, 0, 0)$ требует применения преобразования:

$G = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -\frac{1}{f} & 0 & 1 \end{bmatrix}$

После применения этого преобразования мы наконец получаем эпиполь в бесконечности, поэтому можем вернуться к обычному пространству изображения.

Таким образом, гомография $H_2$, которую мы применяем ко второму изображению для его выравнивания, имеет вид:

$H_2 = T^{-1}GRT$ (23)

Теперь, когда мы нашли допустимую $H_2$, нам нужно найти подходящую гомографию $H_1$ для первого изображения. Мы делаем это путём поиска такого преобразования $H_1$, которое минимизирует сумму квадратов расстояний между соответствующими точками изображений:

$\arg\min_{H_1} \sum_{i} ||H_1p_i - H_2p'_i||^2$

В результате мы получаем пару гомографий ($H_1$, $H_2$), которые позволяют выровнять изображения, сделать эпиполярные линии горизонтальными и упростить поиск соответствий между точками.

Можно доказать, что подходящая гомография $H_1$ имеет следующий вид:

$H_1 = H_A H_2 M$ (25)

где: * $F = [e]\times M$ * $H_A$ — специальная матрица вида:

$H_A = \begin{bmatrix} a_1 & a_2 & a_3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ (26)

Здесь $(a_1, a_2, a_3)$ — компоненты определённого вектора $a$, который будет вычислен позже.

Разберём структуру этого выражения:

Матрица $H_A$ представляет собой линейное преобразование вдоль оси $x$, координаты $y$ и $z$ остаются неизменными. $H_2$ — уже известная гомография для второго изображения
$M$ — вспомогательная матрица, связанная с фундаментальной матрицей $F$
$[e]\times$ — кососимметричная матрица, построенная на векторе $e$

Кососимметричная матрица обладает свойством $A = A^3$ с точностью до масштаба.

Поскольку: * Матрица векторного произведения $[e]\times$ — кососимметричная * Фундаментальная матрица $F$ известна только с точностью до масштаба

Получаем:

$F = [e]\times M = [e]\times[e]\times[e]\times M = [e]\times[e]\times F$ (27)

Отсюда следует:

$M = [e]\times F$ (28)

Важно заметить: если к столбцам $M$ добавить любое скалярное кратное вектора $e$, равенство $F = [e]\times M$ сохраняется.

Поэтому более общий вид $M$:

$M = [e]\times F + ev^T$ (29)

На практике хорошо работает выбор $v^T = [1, 1, 1]$.

Для нахождения $H_1$ нужно вычислить значения вектора $a$ в матрице $H_A$.

Задача сводится к минимизации:

$\arg\min_{H_A} \sum_{i} ||H_A\hat{p}_i - \hat{p}'_i||^2$ (30)

где: * $\hat{p}_i = H_2Mp_i$ * $\hat{p}'_i = H_2p'_i$

При этом $H_2$ и $M$ уже известны.