Линейный классификатор

Андрей Лабинцев

2025-03-05 19:42

Линейный классификатор

Содержание: - Линейная классификация - Параметризованное сопоставление изображений с оценками меток - Интерпретация линейного классификатора - Функция потерь - Потеря машины мультиклассового опорного вектора - Практические соображения - Классификатор Softmax - SVM против Softmax - Интерактивная веб-демонстрация - Краткая сводка - Дополнительные материалы

Линейная классификация

В предыдущем разделе мы рассмотрели задачу классификации изображений, которая заключается в присвоении изображению одного из фиксированного набора категорий. Кроме того, мы описали классификатор k-ближайших соседей (kNN), который присваивает изображениям метки, сравнивая их с (помеченными) изображениями из обучающей выборки. Как мы увидели, у kNN есть ряд недостатков: - Классификатор должен запоминать все обучающие данные и сохранять их для последующего сравнения с тестовыми данными. Это неэффективно с точки зрения использования памяти, поскольку размер наборов данных может легко достигать гигабайтов. - Классификация тестового изображения обходится дорого, поскольку требует сравнения со всеми обучающими изображениями.

Обзор. Теперь мы собираемся разработать более эффективный подход к классификации изображений, который в конечном итоге естественным образом распространится на нейронные сети и свёрточные нейронные сети. Этот подход будет состоять из двух основных компонентов: функции оценки, которая преобразует исходные данные в оценки классов, и функции потерь, которая количественно оценивает соответствие между прогнозируемыми оценками и истинными метками. Затем мы сформулируем это, как задачу оптимизации, в которой мы минимизируем функцию потерь по отношению к параметрам функции оценки.

Параметризованное сопоставление изображений с оценками меток

Первым компонентом этого подхода является определение функции оценки, которая сопоставляет значения пикселей изображения со значениями уверенности для каждого класса. Мы рассмотрим этот подход на конкретном примере. Как и прежде, предположим, что у нас есть набор обучающих изображений $x_i \ in R^D $ каждый из которых связан с меткой $ y_i $. Здесь $i=1 ... N $ и $y_i \in { 1 ... K } $.

То есть у нас есть N примеров (каждый из которых имеет размерность D) и K различных категорий. Например, в CIFAR-10 у нас есть обучающий набор из N = 50 000 изображений, каждое из которых имеет D = 32 x 32 x 3 = 3072 пикселя, и K = 10, так как существует 10 различных классов (собака, кошка, автомобиль и т. д.). Теперь мы определим функцию оценки $f: R^D \mapsto R^K$, которое сопоставляет пиксели необработанного изображения с оценками класса.

Линейный классификатор. В этом модуле мы начнём с, пожалуй, самой простой из возможных функций — линейного отображения:

$$ f(x_i, W, b) = W x_i + b $$

В приведенном выше уравнении мы предполагаем, что изображение $x_i$ все его пиксели сглаживаются до одного вектора-столбца размером [D x 1] . Матрица W (размером [K x D]) и вектор b (размером [K x 1]) являются параметрами функции. В CIFAR-10 $x_i$ содержит все пиксели в i-м изображении, объединённые в один столбец [3072 x 1], W имеет размер [10 x 3072], а b имеет размер [10 x 1], то есть в функцию поступает 3072 числа (исходные значения пикселей), а выходит 10 чисел (оценки классов). Параметры в W часто называют весами, а b называют вектором смещения, потому что он влияет на выходные оценки, но не взаимодействует с фактическими данными $x_i$. Однако вы часто будете слышать, как люди используют термины веса и параметры как взаимозаменяемые. Есть несколько вещей, на которые следует обратить внимание: - Во-первых, обратите внимание, что умножение одной матрицы $W x_1$. Фактически выполняется параллельная оценка 10 отдельных классификаторов (по одному для каждого класса), где каждый классификатор представляет собой строку W. - Обратите также внимание, что мы думаем о входных данных $ (x_i, y_i) $ Мы считаем, что они заданы и неизменны, но мы можем управлять параметрами W, b. Наша цель — настроить их таким образом, чтобы вычисленные оценки соответствовали истинным меткам во всём обучающем наборе данных. Мы подробно рассмотрим, как это сделать, но интуитивно понятно, что мы хотим, чтобы оценка правильного класса была выше, чем оценка неправильных классов. - Преимущество этого подхода заключается в том, что обучающие данные используются для определения параметров W, b, но после завершения обучения мы можем отбросить весь обучающий набор данных и оставить только полученные параметры. Это связано с тем, что новое тестовое изображение можно просто передать в функцию и классифицировать на основе вычисленных показателей. - Наконец, обратите внимание, что классификация тестового изображения включает в себя одно матричное умножение и сложение, что значительно быстрее, чем сравнение тестового изображения со всеми обучающими изображениями.

Предвосхищая вопрос: свёрточные нейронные сети будут сопоставлять пиксели изображения со значениями точно так же, как показано выше, но сопоставление ( f ) будет более сложным и будет содержать больше параметров.

Интерпретация линейного классификатора

Обратите внимание, что линейный классификатор вычисляет оценку класса как взвешенную сумму всех значений пикселей по всем трём цветовым каналам. В зависимости от того, какие именно значения мы задаём для этих весов, функция может любить или не любить (в зависимости от знака каждого веса) определённые цвета в определённых местах изображения. Например, можно представить, что класс «корабль» может быть более вероятным, если по краям изображения много синего (что, скорее всего, соответствует воде). Можно было бы ожидать, что классификатор «корабль» будет иметь множество положительных весовых коэффициентов для синего канала (присутствие синего повышает оценку корабля) и отрицательные весовые коэффициенты для красного/зелёного каналов (присутствие красного/зелёного понижает оценку корабля).

Пример сопоставления изображения с баллами по классам. Для наглядности предположим, что изображение состоит всего из 4 пикселей (4 монохромных пикселя, в этом примере мы не рассматриваем цветовые каналы для краткости) и что у нас есть 3 класса (красный (кошка), зелёный (собака), синий (корабль)). (Уточнение: в частности, цвета здесь просто обозначают 3 класса и не связаны с каналами RGB.) Мы растягиваем пиксели изображения в столбец и выполняем умножение матриц, чтобы получить баллы по каждому классу. Обратите внимание, что этот конкретный набор весовых коэффициентов W совсем не хорош: весовые коэффициенты присваивают нашему изображению кошки очень низкий балл. В частности, этот набор весовых коэффициентов, похоже, убеждён, что видит собаку.

Аналогия изображений с многомерными точками. Поскольку изображения растягиваются в многомерные векторы-столбцы, мы можем интерпретировать каждое изображение как отдельную точку в этом пространстве (например, каждое изображение в CIFAR-10 — это точка в 3072-мерном пространстве размером 32x32x3 пикселя). Аналогично, весь набор данных — это (помеченный) набор точек.

Поскольку мы определили оценку каждого класса как взвешенную сумму всех пикселей изображения, оценка каждого класса является линейной функцией в этом пространстве. Мы не можем визуализировать 3072-мерное пространство, но если мы представим, что все эти измерения сведены к двум, то сможем попытаться визуализировать, что может делать классификатор:

Мультяшное представление пространства изображений, где каждое изображение представляет собой одну точку, а три классификатора визуализированы. На примере классификатора автомобилей (красным цветом) красная линия показывает все точки в пространстве, которые получают нулевой балл за класс автомобилей. Красная стрелка показывает направление увеличения, поэтому все точки справа от красной линии имеют положительные (и линейно возрастающие) баллы, а все точки слева — отрицательные (и линейно убывающие) баллы.

Как мы видели выше, каждый ряд W является классификатором для одного из классов. Геометрическая интерпретация этих чисел заключается в том, что при изменении одного из столбцов W соответствующая линия в пиксельном пространстве будет поворачиваться в разных направлениях. Смещение b. С другой стороны, наши классификаторы позволяют переводить строки. В частности, обратите внимание, что без коэффициентов смещения подстановка $ x_i = 0 $ всегда будет давать нулевой результат независимо от весов, поэтому все линии будут вынуждены пересекать начало координат.

Интерпретация линейных классификаторов как сопоставление шаблонов. Другая интерпретация весовых коэффициентов W заключается в том, что каждая строка W соответствует шаблону (или, как его иногда называют, прототипу) для одного из классов. Оценка каждого класса для изображения затем получается путём сравнения каждого шаблона с изображением с помощью скалярного произведения (или точечного произведения) по очереди, чтобы найти наиболее подходящий. В этой терминологии линейный классификатор выполняет сопоставление шаблонов, которые он изучает. Другой способ взглянуть на это — представить, что мы по-прежнему используем метод ближайшего соседа, но вместо тысяч обучающих изображений мы используем только одно изображение для каждого класса (хотя мы его изучим, и оно не обязательно должно быть одним из изображений в обучающем наборе), и в качестве расстояния мы используем (отрицательное) скалярное произведение вместо расстояния L1 или L2.

Немного забегая вперёд: пример изученных весовых коэффициентов в конце обучения для CIFAR-10. Обратите внимание, что, например, шаблон корабля содержит много синих пикселей, как и ожидалось. Таким образом, этот шаблон будет давать высокий балл при сопоставлении с изображениями кораблей в океане с помощью скалярного произведения.

Кроме того, обратите внимание, что шаблон лошади, по-видимому, содержит двухголовую лошадь, что связано с тем, что в наборе данных есть лошади, смотрящие как влево, так и вправо. Линейный классификатор объединяет эти два вида лошадей в данных в один шаблон. Аналогичным образом, классификатор автомобилей, по-видимому, объединил несколько видов в один шаблон, который должен распознавать автомобили со всех сторон и всех цветов. В частности, этот шаблон оказался красным, что указывает на то, что в наборе данных CIFAR-10 больше красных автомобилей, чем автомобилей любого другого цвета. Линейный классификатор слишком слаб, чтобы правильно распознавать автомобили разных цветов, но, как мы увидим позже, нейронные сети позволят нам выполнить эту задачу. Забегая немного вперёд, скажу, что нейронная сеть сможет создавать промежуточные нейроны в своих скрытых слоях, которые смогут распознавать определённые типы автомобилей (например, зелёный автомобиль, поворачивающий налево, синий автомобиль, поворачивающий вперёд, и т. д.), а нейроны на следующем слое смогут объединять их в более точную оценку автомобиля с помощью взвешенной суммы отдельных детекторов автомобилей.

Уловка с предвзятостью. Прежде чем двигаться дальше, мы хотим упомянуть распространённую упрощающую уловку для представления двух параметров W,b как один. Напомним, что мы определили функцию оценки как:

$$ f(x_i, W, b) = W x_i + b $$

По мере изучения материала становится немного сложнее отслеживать два набора параметров (смещения b и веса W) по отдельности. Часто используемый приём заключается в объединении двух наборов параметров в одну матрицу, которая содержит их оба, путём расширения вектора $ x_i $ с одним дополнительным измерением, которое всегда сохраняет константу 1 - измерение смещения по умолчанию. С дополнительным измерением новая функция оценки упростится до простого умножения матриц: $$ f(x_i, W) = W x_i $$ С нашим примером CIFAR-10, $ x_i $ теперь [3073 x 1] вместо [3072 x 1] — (с дополнительным измерением, содержащим константу 1), и W теперь имеет значение [10 x 3073] вместо [10 x 3072]. Дополнительный столбец, который W теперь соответствует смещению b. Иллюстрация могла бы помочь прояснить ситуацию:

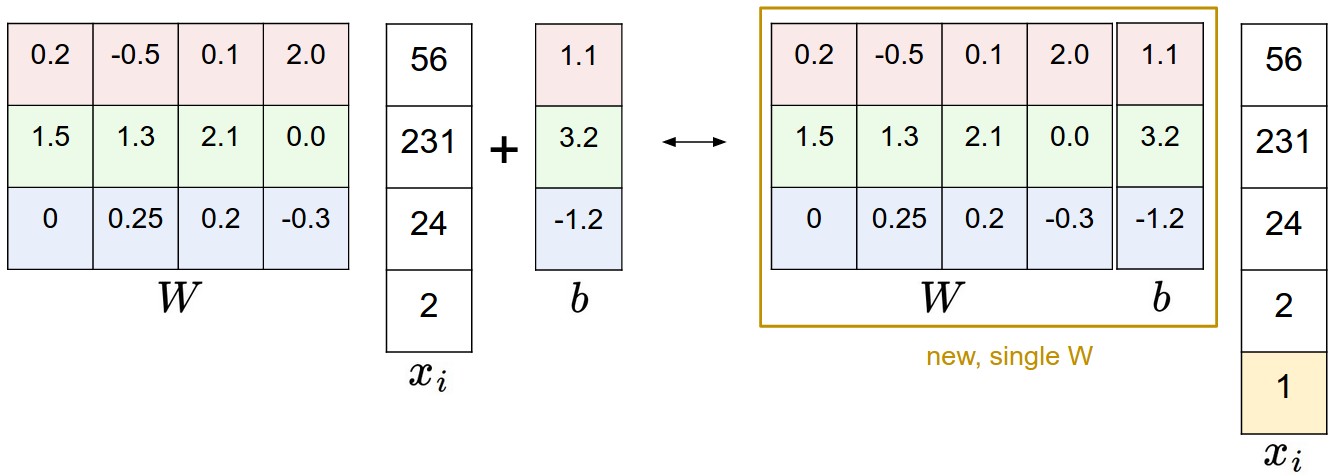
Иллюстрация трюка с предвзятостью. Выполнение матричного умножения с последующим добавлением вектора смещения (слева) эквивалентно добавлению размера смещения с константой 1 ко всем входным векторам и расширению весовой матрицы на 1 столбец - столбец смещения (справа). Таким образом, если мы предварительно обработаем наши данные, добавив единицы ко всем векторам, нам нужно будет выучить только одну матрицу весов вместо двух матриц, которые содержат веса и отклонения.

Предварительная обработка данных изображения. В качестве примечания: в приведённых выше примерах мы использовали необработанные значения пикселей (которые находятся в диапазоне [0…255]). В машинном обучении очень распространена практика нормализации входных признаков (в случае изображений каждый пиксель считается признаком). В частности, важно центрировать данные, вычитая среднее значение из каждого признака. В случае с изображениями это соответствует вычислению среднего значения изображения по обучающим изображениям и вычитанию его из каждого изображения, чтобы получить изображения, в которых пиксели находятся в диапазоне примерно от [-127 до 127]. Далее обычно выполняется предварительная обработка, при которой каждый входной признак масштабируется так, чтобы его значения находились в диапазоне от [-1 до 1]. Из них, пожалуй, более важным является центрирование относительно нуля, но нам придётся подождать с его обоснованием, пока мы не поймём динамику градиентного спуска.

Функция потерь

В предыдущем разделе мы определили функцию преобразования значений пикселей в оценки классов, которая параметризуется набором весовых коэффициентов W. Более того, мы увидели, что у нас нет контроля над данными $(x_i, y_i)$ (это фиксировано и задано), но мы можем управлять этими весами и хотим установить их так, чтобы прогнозируемые оценки классов соответствовали исходным меткам в обучающих данных. Например, если вернуться к примеру с изображением кошки и её оценками для классов «кошка», «собака» и «корабль», то мы увидим, что конкретный набор весов в этом примере был не очень хорошим: мы ввели пиксели, изображающие кошку, но оценка кошки получилась очень низкой (-96,8) по сравнению с другими классами (оценка собаки 437,9, а оценка корабля 61,95). Мы будем измерять степень нашего недовольства такими результатами, как этот, с помощью функции потерь (иногда также называемой функцией затрат или целевой функцией). Интуитивно понятно, что потери будут высокими, если мы плохо справляемся с классификацией обучающих данных, и низкими, если мы хорошо справляемся.

Потеря машины мультиклассового опорного вектора

Существует несколько способов определения параметров функции потерь. В качестве первого примера мы рассмотрим часто используемую функцию потерь, называемую многоклассовой функцией потерь машины опорных векторов (SVM). Функция потерь SVM настроена таким образом, что SVM «хочет», чтобы правильный класс для каждого изображения имел оценку выше, чем у неправильных классов, на некоторую фиксированную величину Δ. Обратите внимание, что иногда полезно очеловечить функции потерь, как мы сделали выше: SVM «хочет» определённого результата в том смысле, что этот результат приведёт к меньшим потерям (что хорошо).

Теперь давайте уточним. Напомним, что для i-го примера нам даны пиксели изображения $ x_i $ и этикетка $ y_i $ которая определяет индекс правильного класса. Функция оценки принимает пиксели и вычисляет вектор $ f(x_i, W) $ оценок за класс, которые мы будем сокращать до s (сокращение от «баллы»). Например, балл за j-й класс — это j-й элемент: $ s_j = f(x_i, W)_j $. Потери многоклассового SVM для i-го примера формализуются следующим образом:

$$ L_i = Σ_{j\neq y_i} max(0, s_j - s_{y_i} + \Delta) $$

Пример. Давайте разберём это на примере, чтобы понять, как это работает. Предположим, что у нас есть три класса, которые получают оценки s=[13,−7,11], и что первый класс является истинным классом (т.е. $ y_i = 0 $ ). Также предположим, что Δ (гиперпараметр, о котором мы вскоре поговорим подробнее) равен 10. Приведенное выше выражение суммирует все неправильные классы ($ j \neq y_i $), таким образом, мы получаем два термина:

$$ L_i = max(0, -7 - 13 + 10) + \max(0, 11 - 13 + 10) $$

Вы видите, что первый член даёт ноль, так как [-7 - 13 + 10] даёт отрицательное число, которое затем округляется до ннля с помощью max(0,−) функция. Мы получаем нулевые потери для этой пары, потому что оценка правильного класса (13) была больше, чем оценка неправильного класса (-7), как минимум на 10. На самом деле разница составляла 20, что намного больше 10, но SVM интересует только то, что разница составляет не менее 10; любая дополнительная разница, превышающая 10, ограничивается нулём с помощью операции max. Второй член вычисляет [11 - 13 + 10], что даёт 8. То есть, даже если правильный класс имел более высокий балл, чем неправильный (13 > 11), он не был выше желаемого значения в 10 баллов. Разница составила всего 2, поэтому проигрыш равен 8 (т. Е. Насколько выше должна быть разница, чтобы соответствовать марже). Таким образом, функция SVM loss запрашивает оценку правильного класса $ y_i = 0 $ быть больше, чем неправильные оценки класса, по крайней мере, на Δ (дельта). Если это не так, мы понесём убытки.

Обратите внимание, что в этом конкретном модуле мы работаем с линейными функциями оценки ( $ f(x_i; W) = W x_i $ ), поэтому мы также можем переписать функцию потерь в этой эквивалентной форме:

$$ L_i = Σ_{j\neq y_i} max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta) $$

где $ w_j$ является j-й строкой W преобразован в столбец. Однако это не обязательно будет так, если мы начнём рассматривать более сложные формы функции оценки f.

Последний термин, который мы упомянем, прежде чем закончить этот раздел, — это нулевой порог max(0,−). Эта функция часто называется потерей от перегиба. Иногда можно услышать, что вместо этого люди используют SVM с квадратичной потерей от перегиба (или L2-SVM), которая имеет вид $max(0,−) ^ 2$ это сильнее6 сказывается на нарушении границ (квадратично, а не линейно). Неквадратичная версия является более стандартной, но в некоторых наборах данных квадратичная функция потерь может работать лучше. Это можно определить во время перекрестной проверки.

Функция потерь количественно определяет наше недовольство прогнозами на обучающем наборе

Многоклассовая машина опорных векторов «хочет», чтобы оценка правильного класса была выше, чем у всех остальных классов, как минимум на величину дельты. Если оценка какого-либо класса находится в красной области (или выше), то будет накоплен убыток. В противном случае убыток будет равен нулю. Наша цель — найти веса, которые одновременно удовлетворят этому ограничению для всех примеров в обучающих данных и обеспечат минимально возможный общий убыток.

Регуляризация. Есть одна ошибка с функцией потерь, которую мы представили выше. Предположим, что у нас есть набор данных и набор параметров W, которые правильно классифицируют каждый пример (т.е. все оценки таковы, что все поля соблюдены, и $L_i = 0)\ для всех i). Проблема в том, что этот набор W не обязательно уникален: может быть много похожих W, которые правильно классифицируют примеры. Один из простых способов увидеть это заключается в том, что если некоторые параметры W правильно классифицируют все примеры (так что потери равны нулю для каждого примера), то любое кратное этим параметрам λW, где λ>1 также даст нулевой убыток, потому что это преобразование равномерно растягивает все величины счета и, следовательно, их абсолютные разности. Например, если разница в оценках между правильным классом и ближайшим неправильным классом равна 15, то умножение всех элементов W на 2 даст новую разницу 30.

Другими словами, мы хотим закодировать некоторое предпочтение для определенного набора весов W по сравнению с другими, чтобы устранить эту двусмысленность. Мы можем сделать это, расширив функцию потерь штрафом за регуляризацию R(W). Наиболее распространенным штрафом за регуляризацию является квадрат нормы L2, который препятствует использованию больших весов с помощью квадратичного штрафа по всем параметрам:

$$ R(W) = \sum_k\sum_l W_{k,l}^2 $$

В приведенном выше выражении мы суммируем все возведенные в квадрат элементы W Обратите внимание, что функция регуляризации не зависит от данных, она зависит только от весовых коэффициентов. Включение штрафа за регуляризацию завершает формирование полной функции потерь многоклассовой машины опорных векторов, которая состоит из двух компонентов: потерь данных (которые представляют собой средние потери $Li$ по всем примерам) и потери от регуляризации. То есть полная потеря многоклассового SVM становится:

$$ L = \underbrace{ \frac{1}{N} \sum_i L_i }\text{потеря данных} + \underbrace{ \lambda R(W) }\text{потеря регуляризации} \\ $$

Или расширить это в его полной форме:

$$ L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)j - f(x_i; W)^2 $$ } + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l

Где N— это количество обучающих примеров. Как видите, мы добавляем штраф за регуляризацию к функции потерь, взвешенной с помощью гиперпараметра λ. Не существует простого способа задать этот гиперпараметр, и обычно он определяется методом перекрёстной проверки.

Помимо мотивации, которую мы привели выше, существует множество желательных свойств, связанных с включением штрафа за регуляризацию, к которым мы вернёмся в следующих разделах. Например, оказывается, что включение штрафа L2 приводит к привлекательному свойству максимального запаса прочности в SVM (если вам интересно, см. CS229 для получения полной информации).

Наиболее привлекательным свойством является то, что штрафные санкции за большие веса, как правило, улучшают обобщение, поскольку это означает, что ни один входной параметр сам по себе не может оказывать очень сильное влияние на оценки. Например, предположим, что у нас есть некоторый входной вектор $x=[1,1,1,1] )) и два весовых вектора__$w1=[1,0,0,0] $, $w2=[0,25,0,25,0,25,0,25] $__. Затем $w_1^Tx = w_2^Tx = 1$. Таким образом, оба вектора весов приводят к одному и тому же скалярному произведению, но штраф L2 $w_1$ равно 1.0, в то время как штраф L2 равен $w_2$ составляет всего 0,5. Следовательно, согласно штрафу L2, вектор весов $w_2$ это предпочтительнее, так как достигается меньшая потеря при регуляризации. Интуитивно понятно, что это происходит потому, что веса в $w_2$ являются более компактными и менее размытыми. Поскольку штраф L2 предпочитает более компактные и менее размытые векторы весов, итоговому классификатору рекомендуется учитывать все входные параметры в небольших количествах, а не несколько входных параметров в очень больших количествах. Как мы увидим далее в этом курсе, этот эффект может улучшить обобщающую способность классификаторов на тестовых изображениях и привести к меньшему переобучению.

Обратите внимание, что смещения не оказывают такого же эффекта, поскольку, в отличие от весовых коэффициентов, они не контролируют силу влияния входного параметра. Поэтому обычно нормализуют только весовые коэффициенты W но не из - за предубеждений b. Однако на практике это часто оказывается несущественным. Наконец, обратите внимание, что из-за штрафа за регуляризацию мы никогда не сможем добиться потери точности, равной 0,0, во всех примерах, потому что это возможно только в патологических условиях W=0.

Код. Вот функция потерь (без регуляризации), реализованная на Python как в не векторизованной, так и в полувекторной форме:

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in range(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment
  ```

Из этого раздела можно сделать вывод, что функция потерь SVM использует особый подход к измерению того, насколько прогнозы на основе обучающих данных соответствуют истинным значениям. Кроме того, делать хорошие прогнозы на основе обучающего набора данных равносильно минимизации функции потерь.  

>Теперь нам нужно придумать способ найти веса, которые минимизируют потери.  

## Практические соображения  

__Устанавливаем дельту__. Обратите внимание, что мы затронули гиперпараметр __Δ__ и его настройка. Какое значение следует установить и нужно ли проводить перекрестную проверку? Оказывается, этот гиперпараметр можно смело устанавливать на __Δ=1.0_ во всех случаях. Гиперпараметры __Δ__ и __λ__: кажется, что это два разных гиперпараметра, но на самом деле они оба управляют одним и тем же компромиссом: компромиссом между потерей данных и потерей от регуляризации в целевой функции. Ключ к пониманию этого заключается в том, что величина весовых коэффициентов __W__ оказывает непосредственное влияние на баллы (и, следовательно, на их разницу): по мере уменьшения всех значений внутри __W__ разница в баллах будет уменьшаться, а по мере увеличения весов разница в баллах будет увеличиваться. Таким образом, точное значение разницы между баллами (например, __Δ=1__ , или __Δ=100__) в некотором смысле бессмысленно, потому что веса могут произвольно уменьшать или увеличивать разницу. Следовательно, единственный реальный компромисс заключается в том, насколько сильно мы позволяем весам увеличиваться (с помощью силы регуляризации __λ__).  

__Связь с бинарной машиной опорных векторов__. Возможно, вы пришли на этот курс, уже имея опыт работы с бинарными машинами опорных векторов, где потери для i-го примера можно записать как:  

$$
L_i = C \max(0, 1 - y_i w^Tx_i) + R(W)
$$  

где __C__ является гиперпараметром, и $y_i \in \\{ -1,1 \\} $. Вы можете убедиться, что представленная в этом разделе формулировка содержит бинарный SVM в качестве частного случая, когда есть только два класса. То есть, если бы у нас было только два класса, то потери сводились бы к бинарному SVM, показанному выше. Кроме того, __C__ в этой формулировке и __λ__ в нашей формулировке контролируется один и тот же компромисс и они связаны через взаимное отношение $C \propto \frac{1}{\lambda}$.  

__Примечание: оптимизация в прямой форме__. Если вы пришли на этот курс, уже имея представление о SVM, то, возможно, слышали о ядрах, двойственных задачах, алгоритме SMO и т. д. В этом курсе (как и в случае с нейронными сетями в целом) мы всегда будем работать с задачами оптимизации в их прямой форме без ограничений. Многие из этих задач технически не являются дифференцируемыми (например, функция max(x,y) не является дифференцируемой, потому что имеет излом при x=y), но на практике это не является проблемой, и обычно используется субградиент.  

Примечание: другие многоклассовые формулировки SVM. Стоит отметить, что многоклассовая формулировка SVM, представленная в этом разделе, является одним из немногих способов формулировки SVM для нескольких классов. Другой часто используемой формой является SVM _«один против всех»_ (OVA), которая обучает независимый бинарный SVM для каждого класса по сравнению со всеми остальными классами. С ней связана, но реже встречается на практике стратегия _«все против всех»_ (AVA). Наша формулировка основана на версии [Weston and Watkins 1999](https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es1999-461.pdf) (pdf), которая является более мощной версией, чем OVA (в том смысле, что вы можете создавать многоклассовые наборы данных, в которых эта версия может обеспечить нулевую потерю данных, а OVA — нет. Если интересно, подробности можно найти в статье). Последняя формулировка, которую вы можете увидеть, — это _структурированный_ SVM, который максимизирует разницу между оценкой правильного класса и оценкой наиболее близкого к нему неправильного класса. Понимание различий между этими формулировками выходит за рамки данного курса. Версия, представленная в этих заметках, безопасна для использования на практике, но, возможно, самая простая стратегия OVA тоже будет работать (как утверждают Рикин и др. в 2004 году в [«В защиту классификации «один против всех»](http://www.jmlr.org/papers/volume5/rifkin04a/rifkin04a.pdf) (pdf)).  

## Классификатор Softmax  

Оказывается, что SVM — один из двух наиболее распространённых классификаторов. Другой популярный вариант — __классификатор Softmax__, у которого другая функция потерь. Если вы раньше слышали о классификаторе бинарной логистической регрессии, то классификатор Softmax — это его обобщение для нескольких классов. В отличие от SVM, который обрабатывает выходные данные $f(x_i,W)$. В качестве (некалиброванных и, возможно, трудно интерпретируемых) оценок для каждого класса классификатор Softmax даёт чуть более понятный результат (нормализованные вероятности классов), а также имеет вероятностную интерпретацию, которую мы вскоре опишем. В классификаторе Softmax функция, отображающая $f(x_i; W) =  W x_i$ остаётся неизменным, но теперь мы интерпретируем эти оценки как ненормированные логарифмические вероятности для каждого класса и заменяем  _потерю от перегиба_ __потерю от перекрёстной энтропии__, которая имеет вид:  

$$
L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}
$$  

где мы используем обозначение __$f_j$__ для обозначения j-го элемента вектора оценок класса __f__. Как и прежде, полная потеря набора данных является средним значением __$L_i$__
 по всем обучающим примерам вместе с термином регуляризации __$R(W)$__. Функция __$f_j(z) = \frac{e^{z_j}}{\sum_k e^{z_k}} $__ называется __функцией softmax__: она принимает вектор произвольных числовых значений  (в $z$) и преобразует его в вектор значений от нуля до единицы, сумма которых равна единице. Полная функция потерь перекрёстной энтропии, включающая функцию softmax, может показаться пугающей, если вы видите её впервые, но её относительно легко объяснить.  

 __С точки зрения теории информации__. _Перекрёстная энтропия_ между «истинным» распределением p
 и предполагаемое распределение __q__ определяется как:  

$$
H(p,q) = - \sum_x p(x) \log q(x)
$$  

Таким образом, классификатор Softmax минимизирует перекрестную энтропию между оцененными вероятностями классов ( $q = e^{f_{y_i}}  / \sum_j e^{f_j} $ как показано выше) и _«истинное»_ распределение, которое в этой интерпретации представляет собой распределение, при котором вся масса вероятностей приходится на правильный класс 
то есть $p = [0, \ldots 1, \ldots, 0]\\ содержит единственную единицу в __$y_i$__-й позиции.). Более того, поскольку кросс-энтропию можно записать в терминах энтропии, а дивергенцию Кульбака-Лейблера - как $H(p,q) = H(p) + D_{KL}(p\|\|q)$, и энтропия дельта - функции __p__ равно нулю, что также эквивалентно минимизации расхождения Кульбака — Лейблера между двумя распределениями (мера расстояния). Другими словами, цель кросс-энтропии _заключается в том_, чтобы прогнозируемое распределение было сосредоточено на правильном ответе.  

__Вероятностная интерпретация__. Глядя на выражение, мы видим, что:  

$$
P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }
$$

может быть интерпретирована как (нормализованная) вероятность, присвоенная правильной метке __$y_i$__ учитывая изображение __$x_i$__ и параметризуется с помощью __W__.Чтобы понять это, вспомните, что классификатор Softmax интерпретирует оценки в выходном векторе __f__, как ненормированные логарифмические вероятности. Возведение этих величин в степень даёт (ненормированные) вероятности, а деление выполняет нормализацию, чтобы сумма вероятностей равнялась единице. Таким образом, в вероятностной интерпретации мы минимизируем отрицательную логарифмическую вероятность правильного класса, что можно интерпретировать как выполнение __оценки максимального правдоподобия__ (MLE). Преимущество такого подхода в том, что теперь мы можем интерпретировать и член регуляризации __R(W)__ в полной функции потерь, исходящей из гауссовского априора по весовой матрице __W__, где вместо MLE мы выполняем оценку _максимального апостериорного значения_ (MAP). Мы приводим эти интерпретации, чтобы помочь вам разобраться, но подробное описание этого вывода выходит за рамки данного курса.  

__Практические вопросы: числовая стабильность__. Когда вы пишете код для вычисления функции Softmax на практике, промежуточные значения$e^{f_{y_i}}$ и $\sum_j e^{f_j}$ может быть очень большим из-за экспоненциальных функций. Деление больших чисел может быть неустойчивым с точки зрения вычислений, поэтому важно использовать приём нормализации. Обратите внимание, что если мы умножим числитель и знаменатель дроби на константу __C__ и подставим его в сумму, получим следующее (математически эквивалентное) выражение:  

$$
\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}
= \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}}
= \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}}
$$  

Мы вольны выбирать стоимость __C__. Это не повлияет ни на один из результатов, но мы можем использовать это значение для повышения численной стабильности вычислений. Обычно выбирают __C__ заключается в том, чтобы установить __$\log C = -\max_j f_j $__. Это просто указывает на то, что мы должны сместить значения внутри вектора __f__ так что наибольшее значение равно нулю. В коде:  


```py
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup

# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer

Возможно, сбивающие с толку соглашения об именовании. Чтобы быть точным, в классификаторе SVM используется потеря шарнира, или также иногда называемая потерей максимальной маржи. Классификатор Softmax использует кросс-энтропийные потери. Классификатор Softmax получил свое название от функции softmax, которая используется для преобразования необработанных оценок класса в нормализованные положительные значения, которые в сумме равны единице, чтобы можно было применить потери от перекрестной энтропии. В частности, обратите внимание, что технически не имеет смысла говорить о «потере при softmax», поскольку softmax — это просто функция сжатия, но это относительно часто используемое сокращение.

SVM против Softmax

Изображение может помочь прояснить разницу между классификаторами Softmax и SVM:

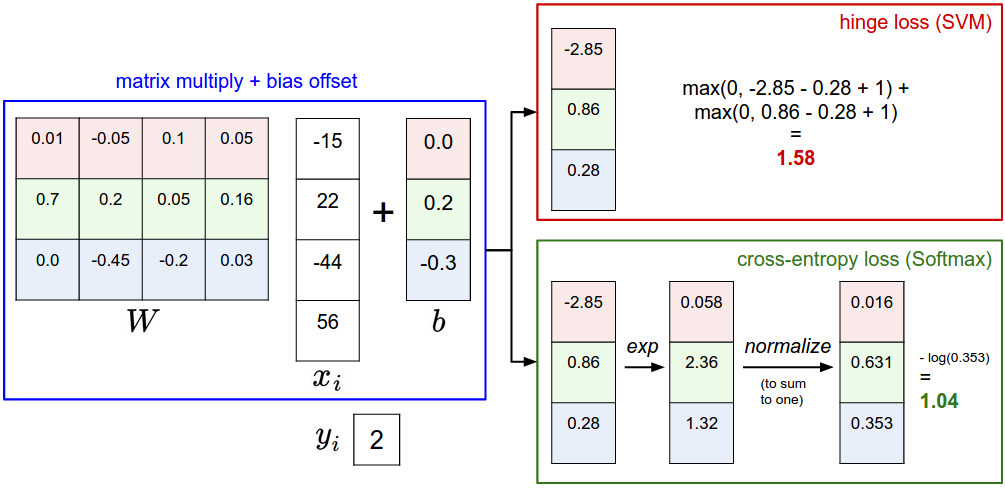
Пример разницы между классификаторами SVM и Softmax для одной точки данных. В обоих случаях мы вычисляем один и тот же вектор оценок f (например, путём умножения матриц в этом разделе). Разница заключается в интерпретации оценок в f: SVM интерпретирует их как оценки классов, и его функция потерь поощряет правильный класс (класс 2, выделен синим цветом) к получению более высокой оценки, чем у других классов. Вместо этого классификатор Softmax интерпретирует баллы как (ненормализованные) логарифмические вероятности для каждого класса, а затем стремится к тому, чтобы (нормализованная) логарифмическая вероятность правильного класса была высокой (эквивалентно, чтобы её отрицательная величина была низкой). Окончательное значение потерь для этого примера составляет 1,58 для SVM и 1,04 (обратите внимание, что это 1,04 с использованием натурального логарифма, а не логарифма по основанию 2 или 10) для классификатора Softmax, но обратите внимание, что эти числа несопоставимы. Они имеют смысл только в сравнении с потерями, рассчитанными для того же классификатора и с теми же данными.

Классификатор Softmax предоставляет «вероятности» для каждого класса. В отличие от SVM, который вычисляет некалиброванные и трудно интерпретируемые оценки для всех классов, классификатор Softmax позволяет вычислять «вероятности» для всех меток. Например, для изображения классификатор SVM может выдать оценки [12,5, 0,6, -23,0] для классов «кошка», «собака» и «корабль». Вместо этого классификатор softmax может вычислить вероятности трёх меток как [0,9, 0,09, 0,01], что позволяет интерпретировать его уверенность в каждом классе. Однако мы взяли слово «вероятности» в кавычки, потому что то, насколько выраженными или размытыми будут эти вероятности, напрямую зависит от силы регуляризации λ, которые вы вводите в систему в качестве входных данных. Например, предположим, что ненормированные логарифмические вероятности для трёх классов равны [1, -2, 0]. Тогда функция softmax вычислит:

$$ [1, -2, 0] \rightarrow [e^1, e^{-2}, e^0] = [2.71, 0.14, 1] \rightarrow [0.7, 0.04, 0.26] $$

Где шаги, предпринятые для возведения в степень и нормализации, суммируются до единицы. Теперь, если сила регуляризации λ был выше, вес W будет больше штрафоваться, и это приведёт к уменьшению весов. Например, предположим, что веса стали в два раза меньше ([0,5, -1, 0]). Теперь softmax будет вычислять:

$$ [0.5, -1, 0] \rightarrow [e^{0.5}, e^{-1}, e^0] = [1.65, 0.37, 1] \rightarrow [0.55, 0.12, 0.33] $$

где вероятности теперь более размыты. Более того, в пределе, когда веса стремятся к малым значениям из-за очень сильной регуляризации __λ__Выходные вероятности были бы почти равномерными. Следовательно, вероятности, вычисляемые классификатором Softmax, лучше рассматривать как степени уверенности, где, как и в случае с SVM, порядок значений интерпретируется, но абсолютные значения (или их разница) технически не интерпретируются.

На практике SVM и Softmax обычно сопоставимы по эффективности. Разница в производительности между SVM и Softmax обычно очень мала, и разные люди по-разному оценивают, какой классификатор работает лучше. По сравнению с классификатором Softmax, SVM является более локальной целью, что можно рассматривать как недостаток или преимущество. Рассмотрим пример, в котором достигаются баллы [10, -2, 3] и где первый класс является правильным. SVM (например, с желаемым запасом прочности Δ=1) увидит, что правильный класс уже имеет оценку выше, чем разница между классами, и вычислит нулевую потерю. SVM не обращает внимания на детали отдельных оценок: если бы они были [10, -100, -100] или [10, 9, 9], SVM было бы всё равно, так как разница в 1 соблюдена и, следовательно, потеря равна нулю. Однако эти сценарии не эквивалентны классификатору Softmax, который привёл бы к гораздо более высоким потерям для оценок [10, 9, 9], чем для [10, -100, -100]. Другими словами, классификатор Softmax никогда не будет полностью удовлетворён полученными оценками: правильный класс всегда может иметь более высокую вероятность, а неправильные классы — более низкую, и потери всегда будут уменьшаться. Однако SVM доволен, если соблюдены границы, и не контролирует точные оценки за пределами этого ограничения. Это можно интуитивно воспринимать как особенность: например, классификатор автомобилей, который, скорее всего, тратит большую часть своих «усилий» на решение сложной задачи по отделению автомобилей от грузовиков, не должен подвергаться влиянию примеров с лягушками, которым он уже присваивает очень низкие баллы и которые, скорее всего, группируются в совершенно другой части облака данных.

Интерактивная веб-демонстрация

Мы написали интерактивную веб-демонстрацию, чтобы помочь вашей интуиции в работе с линейными классификаторами. Демонстрация визуализирует функции потерь, обсуждаемые в этом разделе, с использованием игрушечной трехмерной классификации на 2D-данных. Демонстрационная версия также немного забегает вперед и выполняет оптимизацию, которую мы подробно обсудим в следующем разделе.

Краткая сводка

Подводя итог: - Мы определили функцию оценки от пикселей изображения к оценкам классов (в этом разделе — линейную функцию, которая зависит от весовых коэффициентов W и смещений b). - В отличие от классификатора kNN, преимущество этого параметрического подхода заключается в том, что после определения параметров мы можем отказаться от обучающих данных. Кроме того, прогнозирование для нового тестового изображения выполняется быстро, поскольку требует лишь одного умножения матрицы на W, а не исчерпывающего сравнения с каждым отдельным обучающим примером. - Мы ввели уловку со смещением, которая позволяет нам сложить вектор смещения в весовую матрицу для удобства, чтобы отслеживать только одну матрицу параметров. - Мы определили функцию потерь (мы ввели две часто используемые функции потерь для линейных классификаторов: SVM и Softmax), которая измеряет, насколько заданный набор параметров соответствует истинным меткам в обучающем наборе данных. Мы также увидели, что функция потерь определена таким образом, что хорошие прогнозы на обучающих данных эквивалентны небольшим потерям.

Теперь мы увидели один из способов взять набор изображений и сопоставить каждое из них с баллами классов на основе набора параметров, а также увидели два примера функций потерь, которые можно использовать для оценки качества прогнозов. Но как эффективно определить параметры, которые дают наилучшие (наименьшие) потери? Этот процесс называется оптимизацией, и ему посвящён следующий раздел.

Дополнительные материалы

Эти показания являются необязательными и содержат указания, представляющие интерес: - «Глубокое обучение с использованием линейных машин опорных векторов» от Чарли Танга, 2013 г., представляет некоторые результаты, согласно которым L2SVM превосходит Softmax.