Оптимизация
Оптимизация
Содержание: - Введение - Визуализация функции потерь - Оптимизация - Стратегия #1: Случайный поиск - Стратегия #2: Случайный локальный поиск - Стратегия #3: Следование градиенту - Вычисление градиента - Численно с конечными разностями - Аналитически с помощью исчисления - Градиентный спуск - Краткая сводка
Введение #
В предыдущем разделе мы представили два ключевых компонента в контексте задачи классификации изображений:
- (Параметризованная) функция оценки, сопоставляющая пиксели необработанного изображения с оценками класса (например, линейная функция)
- Функция потерь, которая измеряет качество определенного набора параметров на основе того, насколько хорошо индуцированные оценки согласуются с метками основной истины в обучающих данных. Мы увидели, что существует множество способов и версий этого (например, Softmax/SVM).
В частности, вспомним, что линейная функция имела вид ( f(x_i, W) = W x_i \ и разработанная нами SVM была сформулирована следующим образом:
$$ L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)j - f(x_i; W) + 1) \right] + \alpha R(W) $$
Мы увидели, что настройка параметров \(W\), которые выдавали прогнозы для примера \(x_i\). В соответствии с их основными истинными метками \(y_i\) также будет иметь очень низкий убыток L. Теперь мы представим третий и последний ключевой компонент: оптимизацию. Оптимизация — это процесс нахождения набора параметров (W), которые минимизируют функцию потерь.
Предчувствие: Как только мы поймем, как эти три основных компонента взаимодействуют, мы вернемся к первому компоненту (параметризованному отображению функций) и расширим его до функций, гораздо более сложных, чем линейное отображение: сначала целые нейронные сети, а затем сверточные нейронные сети. Функции потерь и процесс оптимизации останутся относительно неизменными.
Визуализация функции потерь #
Функции потерь, которые мы рассмотрим в этом классе, обычно определяются в очень больших пространствах (например, в CIFAR-10 матрица весов линейного классификатора имеет размер [10 x 3073] для всего 30 730 параметров), что затрудняет их визуализацию. Тем не менее, мы все еще можем получить некоторые интуитивные представления об единице, разрезая пространство высокой размерности вдоль лучей (1 измерение) или вдоль плоскостей (2 измерения). Например, мы можем сгенерировать случайную матрицу весов \(W\), (которая соответствует одной точке в пространстве), затем маршировать по лучу и записывать значение функции потерь по пути. То есть мы можем сгенерировать случайное направление \(W\) и рассчитать потери в этом направлении, оценив \( L(W + a W_1 + b W_2) \) для различных значений \(a\). В результате этого процесса создается простой график со значением \(a\) в качестве оси (X) и значение функции потерь по оси \(Y\). Мы также можем провести ту же процедуру с двумя измерениями, оценив потери \( L(W + a W_1 + b W_2) \) по мере того, как меняются значения \(a, b\). На графике \(a, b\) могут соответствовать осям x и y, а значение функции потерь может быть отображено цветом:
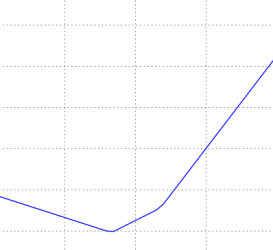
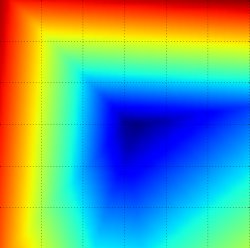
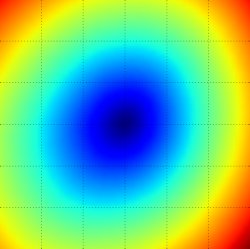
Ландшафт функций потерь для многоклассовой SVM (без регуляризации) для одного единственного примера (сверху, посередине) и для сотни примеров (снизу) в CIFAR-10. Сверху: одномерные потери при изменении только a. Посередине, снизу: двумерный срез потерь, синий = низкие потери, красный = высокие потери. Обратите внимание на кусочно-линейную структуру функции потерь. Потери для нескольких примеров сочетаются со средними, поэтому форма чаши снизу является средним значением многих кусочно-линейных чаш (например, та, что посередине).
Мы можем объяснить кусочно-линейную структуру функции потерь, изучив математические расчеты. В качестве единственного примера мы имеем:
$$ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + 1) \right] $$
Из уравнения ясно, что потеря данных для каждого примера равна сумме (нулевой порог из-за \(\max(0,-)\ функции) линейных функций \(W\). Более того, каждый ряд \(W\) (т.е. \(w_j\)) иногда имеет перед собой положительный знак (когда он соответствует неправильному классу для примера), а иногда отрицательный знак (когда он соответствует правильному классу для этого примера). Чтобы сделать это более явным, рассмотрим простой набор данных, содержащий три одномерные точки и три класса. Полная потеря SVM (без регуляризации) становится следующей:
$$ \begin{align} L_0 = & \max(0, w_1^Tx_0 - w_0^Tx_0 + 1) + \max(0, w_2^Tx_0 - w_0^Tx_0 + 1) \\ L_1 = & \max(0, w_0^Tx_1 - w_1^Tx_1 + 1) + \max(0, w_2^Tx_1 - w_1^Tx_1 + 1) \\ L_2 = & \max(0, w_0^Tx_2 - w_2^Tx_2 + 1) + \max(0, w_1^Tx_2 - w_2^Tx_2 + 1) \\ L = & (L_0 + L_1 + L_2)/3 \end{align} $$
Поскольку эти примеры являются одномерными, данные \(x_i\) и веса \(w_j\) - это цифры. Глядя, например, на \(w_0\), некоторые из приведенных выше членов являются линейными функциями \(w_0\). И каждая из них зажата в точке ноль. Мы можем визуализировать это следующим образом:
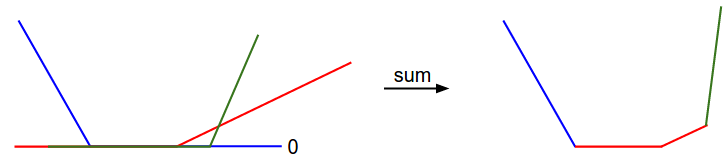
1-мерная иллюстрация потери данных:
Ось x - это один груз
ось y — потери.
В качестве отступления, вы, возможно, догадались по ее чашеобразному виду, что функция стоимости SVM является примером выпуклой функции. Существует большое количество литературы, посвященной эффективной минимизации этих типов функций, и вы также можете пройти курс Стэнфорда по этой теме (выпуклая оптимизация). Как только мы расширим наши функции оценки f для нейронных сетей наши целевые функции станут невыпуклыми, и на приведенных выше визуализациях будут отображаться не чаши, а сложные, ухабистые местности.
Недифференцируемые функции потерь. В качестве технического примечания вы также можете видеть, что изломы в функции потерь (из-за максимальной операции) технически делают функцию потерь недифференцируемой, потому что при этих изломах градиент не определен. Тем не менее, субградиент все еще существует и обычно используется вместо него. В этом классе термины «субградиент» и «градиент» будут использоваться как взаимозаменяемые.
# Оптимизация
Повторимся, что функция потерь позволяет нам количественно оценить качество любого конкретного набора весов W. Цель оптимизации — найти W, которое минимизирует функцию потерь. Теперь мы будем мотивировать и постепенно развивать подход к оптимизации функции потерь. Для тех из вас, кто приходит на этот курс с предыдущим опытом, этот раздел может показаться странным, поскольку рабочий пример, который мы будем использовать (потери SVM), является выпуклой задачей, но имейте в виду, что наша цель состоит в том, чтобы в конечном итоге оптимизировать нейронные сети там, где мы не можем легко использовать ни один из инструментов, разработанных в литературе по выпуклой оптимизации.
Стратегия #1: Первая очень плохая идея: Случайный поиск
Просто проверить, насколько хорош определенный набор параметров W,что очень просто, первая (очень плохая) идея, которая может прийти в голову, — это просто попробовать множество различных случайных весов и отслеживать, что работает лучше всего. Эта процедура может выглядеть следующим образом:
# assume X_train is the data where each column is an example (e.g. 3073 x 50,000) # assume Y_train are the labels (e.g. 1D array of 50,000) # assume the function L evaluates the loss function bestloss = float("inf") # Python assigns the highest possible float value for num in range(1000): W = np.random.randn(10, 3073) * 0.0001 # generate random parameters loss = L(X_train, Y_train, W) # get the loss over the entire training set if loss < bestloss: # keep track of the best solution bestloss = loss bestW = W print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss) # prints: # in attempt 0 the loss was 9.401632, best 9.401632 # in attempt 1 the loss was 8.959668, best 8.959668 # in attempt 2 the loss was 9.044034, best 8.959668 # in attempt 3 the loss was 9.278948, best 8.959668 # in attempt 4 the loss was 8.857370, best 8.857370 # in attempt 5 the loss was 8.943151, best 8.857370 # in attempt 6 the loss was 8.605604, best 8.605604 # ... (trunctated: continues for 1000 lines)
В приведенном выше коде мы видим, что мы опробовали несколько случайных векторов весов W, и некоторые из них работают лучше других. Мы можем взять лучшие веса W, найденные этим поиском, и опробовать их на тестовом наборе:
# Assume X_test is [3073 x 10000], Y_test [10000 x 1] scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples # find the index with max score in each column (the predicted class) Yte_predict = np.argmax(scores, axis = 0) # and calculate accuracy (fraction of predictions that are correct) np.mean(Yte_predict == Yte) # returns 0.1555
При наилучшем W это дает точность около 15,5%. Учитывая, что угадывание классов полностью случайным образом дает только 10%, это не очень плохой результат для такого примитивного решения на основе случайного поиска!
Основная идея: итеративное уточнение. Конечно, оказывается, что мы можем добиться гораздо большего. Основная идея заключается в том, что поиск наилучшего набора весов W является очень сложной или даже невозможной задачей (особенно когда W содержит веса для целых сложных нейронных сетей), но задача уточнения конкретного набора весов W для немного лучшего уровня значительно менее сложна. Другими словами, наш подход будет заключаться в том, чтобы начать со случайной W, а затем итеративно уточнять ее, делая ее немного лучше с каждым разом.
Наша стратегия будет заключаться в том, чтобы начать со случайных весовых коэффициентов и итеративно уточнять их с течением времени, чтобы получить меньшие потери.
Аналогия с туристом с завязанными глазами. Одна из аналогий, которую вы можете найти полезной в будущем - представить, что Вы идете по холмистой местности с повязкой на глазах и пытаетесь добраться до самой низины. В примере с CIFAR-10 холмы имеют размерность 30 730, так как размеры W равны 10 x 3073. В каждой точке холма мы достигаем определенной потери (высоты над уровнем моря).
Стратегия №2: Случайный локальный поиск
Первая стратегия, которая приходит на ум, — это попытаться вытянуть одну ногу в случайном направлении, а затем сделать шаг, только если он ведёт вниз по склону. Конкретно мы начнём со случайного W, генерирующего случайные возмущения δW к нему, и если потеря у возмущенного __W+δW__меньше, мы выполним обновление. Код для этой процедуры выглядит следующим образом:
W = np.random.randn(10, 3073) * 0.001 # generate random starting W bestloss = float("inf") for i in range(1000): step_size = 0.0001 Wtry = W + np.random.randn(10, 3073) * step_size loss = L(Xtr_cols, Ytr, Wtry) if loss < bestloss: W = Wtry bestloss = loss print 'iter %d loss is %f' % (i, bestloss)
При использовании того же количества оценок функции потерь, что и раньше (1000), этот подход обеспечивает точность классификации тестового набора 21,4%. Это лучше, но всё равно неэффективно и требует больших вычислительных мощностей.
Стратегия №3: Следование градиенту
В предыдущем разделе мы пытались найти направление в пространстве весов, которое улучшило бы наш вектор весов (и снизило бы потери). Оказывается, нет необходимости случайным образом искать хорошее направление: мы можем вычислить лучшее направление, в котором нам следует изменить наш вектор весов, чтобы оно гарантированно было направлением наискорейшего спуска (по крайней мере, в пределе, когда размер шага стремится к нулю). Это направление будет связано с градиентом функции потерь. В нашей аналогии с походом этот подход примерно соответствует тому, чтобы почувствовать наклон холма под ногами и идти в направлении, которое кажется наиболее крутым.
В одномерных функциях наклон — это мгновенная скорость изменения функции в любой интересующей вас точке. Градиент — это обобщение наклона для функций, которые принимают не одно число, а вектор чисел. Кроме того, градиент — это просто вектор наклонов (более известных как производные) для каждого измерения во входном пространстве. Математическое выражение для производной одномерной функции по входным данным выглядит так:
$$ \frac{df(x)}{dx} = \lim_{h\ \to 0} \frac{f(x + h) - f(x)}{h} $$
Когда интересующие нас функции принимают вектор чисел вместо одного числа, мы называем производные частными производными, а градиент — это просто вектор частных производных по каждому измерению.
Вычисление градиента
Существует два способа вычисления градиента: медленный, приблизительный, но простой (численный градиент) и быстрый, точный, но более подверженный ошибкам способ, требующий математических вычислений (аналитический градиент). Сейчас мы рассмотрим оба способа.
Вычисление градиента численно с конечными разностями
Приведённая выше формула позволяет вычислить градиент численно. Вот универсальная функция, которая принимает градиент f и вектор x для вычисления функции и возвращает градиент f в точке x:
def eval_numerical_gradient(f, x): """ a naive implementation of numerical gradient of f at x - f should be a function that takes a single argument - x is the point (numpy array) to evaluate the gradient at """ fx = f(x) # evaluate function value at original point grad = np.zeros(x.shape) h = 0.00001 # iterate over all indexes in x it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) while not it.finished: # evaluate function at x+h ix = it.multi_index old_value = x[ix] x[ix] = old_value + h # increment by h fxh = f(x) # evalute f(x + h) x[ix] = old_value # restore to previous value (very important!) # compute the partial derivative grad[ix] = (fxh - fx) / h # the slope it.iternext() # step to next dimension return grad
В соответствии с формулой градиента, которую мы привели выше, приведённый код перебирает все параметры один за другим, вносит небольшое изменение h в этом параметре и вычисляет частную производную функции потерь по этому параметру, определяя, насколько изменилась функция. Переменная grad в итоге содержит полный градиент.
Практические соображения. Обратите внимание, что в математической формулировке градиент определяется в пределе, когда h стремится к нулю, но на практике часто достаточно использовать очень маленькое значение (например, 1e-5, как показано в примере). В идеале нужно использовать наименьший размер шага, который не приводит к численным проблемам. Кроме того, на практике часто лучше вычислять численный градиент с помощью формулы центрированной разности: [f(x+h)−f(x−h)]/2h. Смотрите wiki для получения подробной информации.
Мы можем использовать приведённую выше функцию для вычисления градиента в любой точке и для любой функции. Давайте вычислим градиент функции потерь CIFAR-10 в некоторой случайной точке в пространстве весов:
# to use the generic code above we want a function that takes a single argument # (the weights in our case) so we close over X_train and Y_train def CIFAR10_loss_fun(W): return L(X_train, Y_train, W) W = np.random.rand(10, 3073) * 0.001 # random weight vector df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradient
Градиент показывает наклон функции потерь по каждому измерению, и мы можем использовать его для обновления:
loss_original = CIFAR10_loss_fun(W) # the original loss print 'original loss: %f' % (loss_original, ) # lets see the effect of multiple step sizes for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]: step_size = 10 ** step_size_log W_new = W - step_size * df # new position in the weight space loss_new = CIFAR10_loss_fun(W_new) print 'for step size %f new loss: %f' % (step_size, loss_new) # prints: # original loss: 2.200718 # for step size 1.000000e-10 new loss: 2.200652 # for step size 1.000000e-09 new loss: 2.200057 # for step size 1.000000e-08 new loss: 2.194116 # for step size 1.000000e-07 new loss: 2.135493 # for step size 1.000000e-06 new loss: 1.647802 # for step size 1.000000e-05 new loss: 2.844355 # for step size 1.000000e-04 new loss: 25.558142 # for step size 1.000000e-03 new loss: 254.086573 # for step size 1.000000e-02 new loss: 2539.370888 # for step size 1.000000e-01 new loss: 25392.214036
Обновление в направлении отрицательного градиента. В приведенном выше коде обратите внимание, что для вычисления W_new мы выполняем обновление в направлении отрицательного градиента df, поскольку хотим, чтобы наша функция потерь уменьшалась, а не увеличивалась.
Влияние размера шага. Градиент показывает нам направление, в котором функция возрастает наиболее быстро, но не говорит нам, насколько далеко в этом направлении мы должны продвинуться. Как мы увидим далее в курсе, выбор размера шага (также называемого скоростью обучения) станет одним из самых важных (и самых сложных) параметров при обучении нейронной сети. В нашей аналогии со спуском с холма вслепую мы чувствуем, что склон под нашими ногами наклонён в каком-то направлении, но длина шага, который мы должны сделать, неизвестна. Если мы будем осторожно переставлять ноги, то сможем рассчитывать на последовательный, но очень медленный прогресс (это соответствует небольшому размеру шага). И наоборот, мы можем сделать большой уверенный шаг, чтобы спуститься быстрее, но это может не окупиться. Как вы можете видеть в примере кода выше, в какой-то момент более длинный шаг приведёт к большим потерям, так как мы «перешагнём».
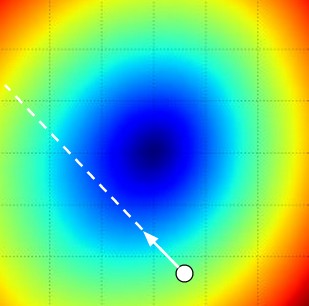
Визуализация влияния размера шага. Мы начинаем с какой-то конкретной точки W и вычисляем градиент (или, скорее, его отрицательную величину — белую стрелку), который указывает направление наиболее резкого снижения функции потерь. Маленькие шаги, скорее всего, приведут к стабильному, но медленному прогрессу. Большие шаги могут привести к более быстрому прогрессу, но они более рискованны. Обратите внимание, что в конечном итоге при большом размере шага мы совершим ошибку и увеличим потери. Размер шага (или, как мы позже назовём его, скорость обучения) станет одним из важнейших гиперпараметров, которые нам придётся тщательно настраивать.
Проблема эффективности. Возможно, вы заметили, что вычисление численного градиента имеет сложность, линейную по отношению к количеству параметров. В нашем примере у нас было 30 730 параметров, и поэтому для вычисления градиента и обновления только одного параметра нам пришлось выполнить 30 731 вычисление функции потерь. Эта проблема усугубляется тем, что современные нейронные сети могут легко содержать десятки миллионов параметров. Очевидно, что эта стратегия не масштабируется, и нам нужно что-то получше.
Вычисление градиента аналитически с помощью математического анализа
Численный градиент очень просто вычислить с помощью конечно-разностного приближения, но его недостатком является то, что он является приблизительным (поскольку нам нужно выбрать небольшое значение h, в то время как истинный градиент определяется как предел, когда h стремится к нулю), а также то, что его вычисление требует больших вычислительных мощностей. Второй способ вычисления градиента — аналитический, с использованием математического анализа, который позволяет вывести прямую формулу для градиента (без приближений), которая также очень быстро вычисляется. Однако, в отличие от численного градиента, его реализация может быть более подвержена ошибкам, поэтому на практике очень часто вычисляют аналитический градиент и сравнивают его с численным градиентом, чтобы проверить правильность реализации. Это называется проверкой градиента.
Давайте рассмотрим пример функции потерь SVM для одной точки данных:
$$ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + \Delta) \right] $$
Мы можем дифференцировать функцию по весовым коэффициентам. Например, взяв градиент по \(w_{y_i}\) мы получаем:
$$ \nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i $$
где \(\mathbb{1}\)- это индикаторная функция, которая принимает значение 1, если условие внутри истинно, и 0 в противном случае. Хотя это выражение может показаться пугающим, когда вы записываете его, при реализации в коде вы просто подсчитываете количество классов, которые не соответствуют желаемой погрешности (и, следовательно, влияют на функцию потерь), а затем вектор данных \(x_i\), умноженное на это число — это градиент. Обратите внимание, что это градиент только по отношению к строке W, а это соответствует правильному классу. Для других строк, где j≠\(y_i\) градиент равен:
$$ \nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i $$
Как только вы получите выражение для градиента, будет несложно реализовать эти выражения и использовать их для обновления градиента.
Градиентный спуск
Теперь, когда мы можем вычислить градиент функции потерь, процедура многократного вычисления градиента, а затем обновления параметров, называется градиентным спуском. Его простая версия выглядит следующим образом:
# Vanilla Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter update
Этот простой цикл лежит в основе всех библиотек нейронных сетей. Существуют и другие способы оптимизации (например, LBFGS), но градиентный спуск в настоящее время является наиболее распространённым и устоявшимся способом оптимизации функций потерь нейронных сетей. В ходе курса мы рассмотрим некоторые детали этого цикла (например, точное уравнение обновления), но основная идея следования за градиентом до тех пор, пока нас не удовлетворят результаты, останется прежней.
Мини-пакетный градиентный спуск. В крупномасштабных приложениях (таких как ILSVRC) обучающие данные могут насчитывать миллионы примеров. Следовательно, вычисление полной функции потерь по всему обучающему набору данных для выполнения только одного обновления параметров кажется нецелесообразным. Очень распространённым подходом к решению этой проблемы является вычисление градиента по пакетам обучающих данных. Например, в современных сверточных нейронных сетях типичная партия содержит 256 примеров из всего обучающего набора, состоящего 1,2 миллиона примеров. Затем эта партия используется для обновления параметров:
# Vanilla Minibatch Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter update
Причина, по которой это работает, заключается в том, что примеры в обучающих данных взаимосвязаны. Чтобы понять это, рассмотрим крайний случай, когда все 1,2 миллиона изображений в ILSVRC на самом деле являются точными дубликатами всего 1000 уникальных изображений (по одному для каждого класса, или, другими словами, 1200 идентичных копий каждого изображения). Тогда очевидно, что градиенты, которые мы вычислили бы для всех 1200 идентичных копий, были бы одинаковыми, и если бы мы усреднили потерю данных по всем 1,2 миллионам изображений, то получили бы точно такую же потерю, как если бы мы оценивали только небольшое подмножество из 1000 изображений. На практике, конечно, набор данных не содержит дубликатов изображений, и градиент от мини-пакета является хорошим приближением к градиенту полной задачи. Таким образом, на практике можно добиться гораздо более быстрой сходимости, оценивая градиенты мини-пакетов для более частого обновления параметров.
Крайним случаем этого является ситуация, когда мини-пакет содержит только один пример. Этот процесс называется стохастическим градиентным спуском (SGD) (или иногда онлайн-градиентным спуском). Это относительно редкое явление, потому что на практике из-за оптимизации кода с помощью векторизации гораздо эффективнее вычислять градиент для 100 примеров, чем градиент для одного примера 100 раз. Несмотря на то, что SGD технически подразумевает использование одного примера для оценки градиента, вы услышите, как люди используют термин SGD даже при упоминании градиентного спуска с мини-пакетами (т. е. редко можно встретить упоминания MGD для «градиентного спуска с мини-пакетами» или BGD для «пакетного градиентного спуска»), где обычно предполагается использование мини-пакетов. Размер мини-пакета является гиперпараметром, но его нечасто проверяют на перекрёстной проверке. Обычно это зависит от ограничений памяти (если они есть) или устанавливается на какое-то значение, например 32, 64 или 128. На практике мы используем степени двойки, потому что многие реализации векторизованных операций работают быстрее, если размер входных данных равен степени двойки.
Краткая сводка
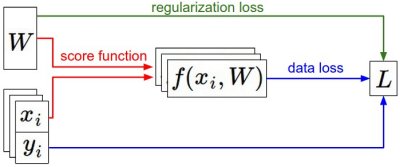
Краткое описание информационного потока. Набор данных, состоящий из пар (x,y), задан и неизменен. Веса изначально являются случайными числами и могут меняться. Во время прямого прохода функция оценки вычисляет оценки классов, которые сохраняются в векторе f. Функция потерь содержит два компонента: Функция потерь данных вычисляет соответствие между оценками f и метками y. Функция потерь регуляризации зависит только от весов. Во время градиентного спуска мы вычисляем градиент по весовым коэффициентам (и, при желании, по данным) и используем его для обновления параметров во время градиентного спуска.
В этом разделе: - Мы представили функцию потерь как многомерный ландшафт оптимизации, в котором мы пытаемся достичь дна. Рабочая аналогия, которую мы разработали, — это турист с завязанными глазами, который хочет добраться до дна. В частности, мы увидели, что функция стоимости SVM является кусочно-линейной и имеет форму чаши. - Мы обосновали идею оптимизации функции потерь с помощью итеративного уточнения, при котором мы начинаем со случайного набора весовых коэффициентов и шаг за шагом уточняем их, пока потери не будут минимизированы. - Мы увидели, что градиент функции указывает направление наискорейшего подъёма, и обсудили простой, но неэффективный способ его численного вычисления с помощью конечно-разностной аппроксимации (конечно-разностная аппроксимация — это значение h, используемое при вычислении численного градиента). - Мы увидели, что для обновления параметров требуется сложная настройка размера шага (или скорости обучения), который должен быть установлен правильно: если он слишком мал, прогресс будет стабильным, но медленным. Если он слишком велик, прогресс может быть быстрее, но более рискованным. Мы рассмотрим этот компромисс более подробно в следующих разделах. - Мы обсудили компромиссы между вычислением численного и аналитического градиента. Численный градиент прост, но он приблизителен и требует больших вычислительных затрат. Аналитический градиент точен, быстро вычисляется, но более подвержен ошибкам, поскольку требует вычисления градиента с помощью математики. Поэтому на практике мы всегда используем аналитический градиент, а затем выполняем проверку градиента, в ходе которой его реализация сравнивается с численным градиентом. - Мы представили алгоритм градиентного спуска, который итеративно вычисляет градиент и выполняет обновление параметров в цикле.
Далее: основной вывод из этого раздела заключается в том, что способность вычислять градиент функции потерь по отношению к её весовым коэффициентам (и иметь некоторое интуитивное представление об этом) — самый важный навык, необходимый для проектирования, обучения и понимания нейронных сетей. В следующем разделе мы научимся вычислять градиент аналитически с помощью правила дифференцирования сложной функции, также известного как обратное распространение ошибки. Это позволит нам эффективно оптимизировать относительно произвольные функции потерь, которые используются во всех видах нейронных сетей, включая свёрточные нейронные сети.