Измерение углов

Введение

На предыдущих лекциях мы обсуждали, как можно преобразовывать точки из реального трёхмерного мира в цифровые изображения, используя внешние и внутренние характеристики камер. Мы рассмотрели, как можно использовать известную структуру калибровочной установки и соответствующие изображения для определения характеристик камеры.

Теперь мы обратимся к смежной проблеме: можно ли восстановить известную структуру трёхмерного мира, если у нас есть единственное изображение и известны свойства камеры, которой это изображение было сделано? И наконец мы рассмотрим алгоритм калибровки камеры и измерения углов между плоскостями на одиночном изображении.

1. Преобразования в 2D пространстве

Чтобы лучше понять, как мы можем извлекать информацию из изображений, сначала необходимо разобраться с различными преобразованиями в двумерном пространстве.

Изометрические преобразования — это преобразования, сохраняющие расстояния. В своей базовой форме изометрия может быть описана как вращение $R$ и перенос $t$. Математически они определяются следующим образом:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

где $(x', y', 1)^T$ — точка, полученная после изометрического преобразования.

Преобразования подобия — это преобразования, сохраняющие форму. Интуитивно они могут выполнять всё то же, что и изометрические преобразования, плюс масштабирование. Математически они обозначаются так:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} SR & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $

$ S = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix}$

Преобразования подобия сохраняют форму объектов, а значит, сохраняют:
Отношения длин отрезков
Величины углов

Важно отметить, что любое изометрическое преобразование является частным случаем преобразования подобия при $s = 1$. Однако обратное утверждение неверно.

Аффинные преобразования сохраняют:
Точки
Прямые линии
* Параллельность прямых

Для вектора $v$ аффинное преобразование $T$ определяется как: $T(v) = Av + t$, где $A$ — линейное преобразование пространства $R^n$

В однородных координатах аффинные преобразования записываются так:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Из этого уравнения видно, что все преобразования подобия (и, следовательно, изометрии) являются частным случаем аффинных преобразований.

Проективные преобразования (или гомографии) — это преобразования, которые переводят прямые в прямые, но не обязательно сохраняют параллельность.

В однородных координатах проективные преобразования представляются как:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ v & b \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Это представление является обобщением аффинных преобразований за счёт добавления вектора $v$, который вводит дополнительные степени свободы.

Несмотря на то, что проективные преобразования не сохраняют параллельность, они сохраняют:
Коллинеарность точек (прямые переходят в прямые)
Перекрестное отношение четырёх коллинеарных точек.

Перекрестное отношение четырёх точек $P_1, P_2, P_3, P_4$, лежащих на одной прямой, вычисляется по формуле:

$cross\ ratio = \frac{||P_3 - P_1||\ ||P_4 - P_2||}{||P_3 - P_2||\ ||P_4 - P_1||}$ (1)

Доказательство инвариантности перекрестного отношения при проективных преобразованиях предлагается выполнить в качестве учебного упражнения.

2. Точки и прямые в бесконечности

Прямые играют важную роль в определении структуры изображений, поэтому важно понимать их представление как в 2D, так и в 3D пространстве.

Прямая на плоскости может быть представлена однородным вектором $\ell = \begin{bmatrix} a & b & c \end{bmatrix}^T$.

Отношение $-\frac{a}{b}$ определяет наклон прямой, а отношение $-\frac{c}{b}$ — точку пересечения с осью $y$.

Для любой точки, лежащей на прямой, справедливо уравнение:

$\forall p = \begin{bmatrix} x \\ y \end{bmatrix} \in \ell, \quad \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0$ (2)

Пересечение прямых
В общем случае две прямые $\ell$ и $\ell'$ пересекаются в точке $x$, которая определяется как векторное произведение этих прямых.

• Доказательство: если две прямые пересекаются, точка пересечения $x$ должна лежать на обеих прямых. Следовательно, $x^T\ell = 0$ и $x^T\ell' = 0$. Если мы положим $x = \ell \times \ell'$, то по определению векторного произведения вектор $x$ будет ортогонален обоим векторам $\ell$ и $\ell'$.

Параллельные прямые
В школьной геометрии считается, что параллельные прямые не пересекаются. Однако в однородных координатах можно сказать, что они пересекаются в бесконечности.

Рассмотрим две параллельные прямые $\ell$ и $\ell'$. Когда прямые параллельны, их наклоны равны: $\frac{a}{b} = \frac{a'}{b'}$. Если вычислить точку пересечения в однородных координатах, получим:

$\ell \times \ell' \propto \begin{bmatrix} b \\ -a \\ 0 \end{bmatrix} = x_\infty$ (3)

Это подтверждает, что параллельные прямые пересекаются в бесконечности. Точка пересечения параллельных прямых в бесконечности называется идеальной точкой.

В однородных координатах идеальная точка в бесконечности представляется как:

$\begin{bmatrix} x \ y \ 0 \end{bmatrix}^T$

Свойство идеальных точек Все параллельные прямые с одинаковым наклоном $-\frac{a}{b}$ проходят через идеальную точку:

$\ell^T x_\infty = \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} b \\ -a \\ 0 \end{bmatrix} = 0$ (4)

Бесконечно удалённые точки позволяют определить прямую в бесконечности. Рассмотрим несколько пар параллельных прямых. Каждая пара пересекается в своей точке бесконечности $x_{\infty,i}$. Прямая $\ell_\infty$, проходящая через все эти точки, должна удовлетворять условию:

$\forall i, \ell_\infty^T x_{\infty,i} = 0$

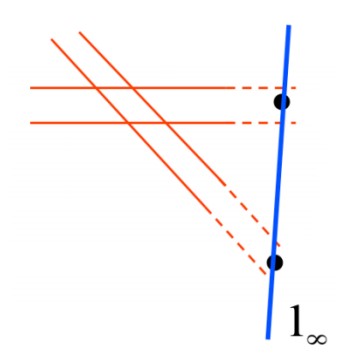
Рисунок 1: Точки в бесконечности образуют прямые в бесконечности

Такая прямая имеет вид $\ell_\infty = \begin{bmatrix} 0 & 0 & c \end{bmatrix}^T$. Поскольку $c$ — произвольное значение, можно принять:

$\ell_\infty = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^T$

Проективное преобразование точки в бесконечности:

При применении проективного преобразования $H$ к точке в бесконечности $p_\infty$ получаем:

$p' = Hp_\infty = \begin{bmatrix} A & t \\ v & b \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix}$ (5)

Заметим, что последний элемент $p'$ может стать ненулевым. Это означает, что проективное преобразование обычно переводит точки в бесконечности в точки, которые уже не находятся в бесконечности. Т.е. имеют конечные евклидовы координаты, пусть и за пределами изображения.

Аффинные преобразования ведут себя иначе и всегда переводят точку из бесконечности в бесконечность:

$p' = Hp_\infty = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y \\ 0 \end{bmatrix}$ (6)

Преобразование прямых

При применении проективного преобразования $H$ к прямой $\ell$ получаем новую прямую $\ell'$. Все точки $x$, лежащие на прямой, должны удовлетворять условию $x^T\ell = 0$. В преобразованном пространстве прямые переходят в прямые, то есть $x'^T\ell' = 0$. Используя свойство тождественного преобразования, получаем:

$x^TI\ell = x^TH^TH^{-T}\ell = 0$

При применении проективного преобразования к прямой происходит преобразование всех точек, лежащих на ней. Если $x$ — точка исходной прямой, то после преобразования получаем:

$x' = Hx$

Используя это преобразование, можно записать:

$x^TH^TH^{-T}\ell = x'^T\ell'$,

откуда следует, что проективное преобразование прямой имеет вид:

$\ell' = H^{-T}\ell$

Важные выводы:
При проективном преобразовании прямая в бесконечности не обязательно переходит в другую прямую в бесконечности
В отличие от этого, аффинные преобразования сохраняют прямые в бесконечности, переводя их в прямые в бесконечности.

Эти свойства имеют важное значение для понимания того, как различные типы преобразований влияют на структуру изображения и геометрию сцены. Особенно это касается работы с бесконечно удалёнными точками и прямыми, которые играют ключевую роль в проективной геометрии и компьютерном зрении.

Таким образом, при работе с проективными преобразованиями необходимо учитывать, что они могут существенно изменять геометрию сцены, в том числе расположение прямых и точек в бесконечности, в то время как аффинные преобразования сохраняют некоторые геометрические свойства.

3. Точки и линии схода

В трёхмерном пространстве вводится понятие плоскости, которая представляется вектором $\begin{bmatrix} a & b & c & d \end{bmatrix}^T$. Здесь $(a, b, c)$ образуют вектор нормали, а $d$ — расстояние от начала координат до плоскости в направлении этого вектора. Формально плоскость определяется как множество точек $x$, удовлетворяющих уравнению:

$x^T \begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} = ax_1 + bx_2 + cx_3 + d = 0$ (7)

Прямые в 3D определяются как пересечение двух плоскостей. Они имеют четыре степени свободы (точка пересечения и наклоны в трёх измерениях).

Точки в бесконечности в 3D определяются как точки пересечения параллельных прямых. При проективном преобразовании таких точек получается точка схода $p_\infty$ на плоскости изображения.

Существует полезное соотношение между параллельными прямыми в 3D, их точкой схода на изображении и параметрами камеры $K$, $R$, $T$.

Пусть $d = (a, b, c)$ — направление набора параллельных прямых в системе координат камеры. Тогда точка схода $v$ определяется как:

$v = Kd$ (8)

Отсюда можно выразить направление $d$:

$d = \frac{K^{-1}v}{|K^{-1}v|}$ (9)

Линия горизонта (или линия схода) $l_{horiz}$ — это проекция линии в бесконечности на плоскость изображения. Она проходит через соответствующие точки схода на изображении и вычисляется по формуле:

$l_{horiz} = H^{-T}P l_\infty$ (10)

Точки и линии схода являются важными инструментами для анализа структуры сцены и определения параметров камеры по изображению, т.к. они позволяют восстанавливать трёхмерную геометрию по двумерной проекции.

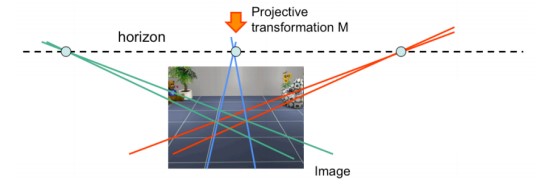
Линия горизонта позволяет нам интуитивно определять свойства изображения, которые могут быть неочевидны с математической точки зрения. Например, линии на земле не выглядят параллельными на изображении (как показано на рисунке 2), но интуитивно мы все же понимаем, что в трёхмерном пространстве они параллельны.

Линия горизонта позволяет вычислять важные характеристики сцены. Существует интересное соотношение между нормалью $n$ плоскости в 3D и соответствующей линией горизонта $l_{horiz}$ на изображении:

$n = K^Tl_{horiz}$ (11)

Это означает, что если мы можем определить линию горизонта, связанную с плоскостью, и знаем внутренние характеристики камеры $K$, мы можем оценить ориентацию этой плоскости.

Теперь давайте рассмотрим понятие плоскость в бесконечности.

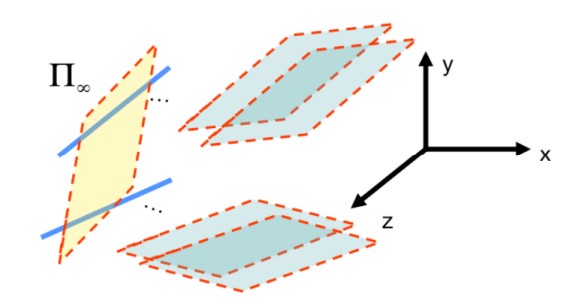
Рисунок 3: Плоскость в бесконечности

Эта плоскость определяется набором из двух или более линий схода. В однородных координатах плоскость описывается вектором:

$Π_\infty = \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}^T$

Плоскость в бесконечности поможет нам понять важное свойство, связывающее линии и плоскости в 3D с соответствующими точками и линиями схода на плоскости изображения.

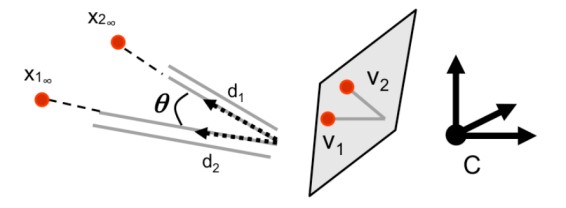
Рисунок 4: Определение угла между линиями

Пусть две пары параллельных линий в 3D имеют направления $d_1$ и $d_2$, связанные с точками в бесконечности $x_{1,\infty}$ и $x_{2,\infty}$. Пусть $v_1$ и $v_2$ — соответствующие точки схода. Тогда угол $θ$ между $d_1$ и $d_2$ определяется по формуле:

$\cos θ = \frac{d_1 \cdot d_2}{|d_1||d_2|} = \frac{v_1^T \omega v_2}{\sqrt{v_1^T \omega v_1} \sqrt{v_2^T \omega v_2}}$ (12)

где $\omega = (KK^T)^{-1}$.

Матрица $\omega$ определяется через матрицу камеры $K$ следующим образом:

$\omega = (K K^T)^{-1}$

Эта матрица имеет важные свойства:

1. Симметричность: матрица $\omega$ является симметричной, так как $K K^T$ — симметричная матрица, а обратная к симметричной матрице также симметрична

2. Связь с параметрами камеры: содержит информацию о внутренних параметрах камеры, зависит от фокусных расстояний, координат главной точки и коэффициента скоса (skew).

3. При стандартных предположениях о камере (нулевой скос, квадратные пиксели) матрица $\omega$ имеет вид:

$\omega = \begin{bmatrix} \omega_1 & 0 & \omega_4 \\ 0 & \omega_1 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6 \end{bmatrix}$

Матрица $\omega$ определяется с точностью до масштабного множителя, что влияет на количество независимых переменных при решении системы уравнений. Это свойство учитывается при калибровке камеры и восстановлении 3D-структуры сцены.

Это соотношение показывает, как можно определить угол между направлениями в пространстве, используя только точки схода на изображении и параметры камеры.

И наконец, расширим рассмотренную концепцию на случай трёхмерных плоскостей, чтобы установить связь между различными плоскостями в 3D пространстве.

Для любой плоскости мы можем:
Вычислить соответствующую линию горизонта $l_{horiz}$
Определить нормаль к плоскости $n = K^\ l_{horiz}$

Угол $\theta$ между двумя плоскостями можно определить через угол между их нормалями $n_1$ и $n_2$. Рассмотрим две плоскости с линиями горизонта $l_1$ и $l_2$ соответственно. Угол между нормалями этих плоскостей определяется формулой:

$\cos \theta = \frac{n_1 \cdot n_2}{|n_1||n_2|} = \frac{l_1^T \omega^{-1} l_2}{\sqrt{l_1^T \omega^{-1} l_1} \sqrt{l_2^T \omega^{-1} l_2}}$ (13)

Таким образом, используя линии горизонта и параметры камеры, мы можем восстанавливать пространственные отношения между плоскостями в сцене, что является важным инструментом в компьютерном зрении и трёхмерной реконструкции.

4. Алгоритм калибровки камеры и измерения углов

Рассмотрим пример решения задачи калибровки камеры по одной фотографии. Для этого нам понадобится изображение трёхмерного мира, на котором мы можем выполнить следующие операции:
Определить три плоскости и на каждой из этих плоскостей пару параллельных линий
Идентифицировать точки схода $v_1$ $v_2$ и $v_3$
* Использовать априорное знание и том, что плоскости перпендикулярны в 3D пространстве.

Рисунок 5: Точки схода на перпендикулярных плоскостях

Из уравнения (12) мы знаем, что для перпендикулярных плоскостей выполняется соотношение $v_1\omega v_2 = 0$.

Если мы имеем три точки схода для трех взаимно перпендикулярной плоскости, то получаем систему:

$v_1\omega v_2 = 0$
$v_1\omega v_3 = 0$
$v_2\omega v_3 = 0$

При предположении об отсутствии скоса камеры и квадратных пикселях, мы можем решить эту систему относительно элементов матрицы $\omega_1, \omega_4, \omega_5, \omega_6$ (с точностью до масштаба).

Зная матрицу $\omega$, можно вычислить элементы матрицы камеры $K$ с помощью разложения Холецкого.

Таким образом, мы выполняем калибровку камеры всего по одному изображению. После определения $K$ мы можем восстановить 3D-геометрию сцены, вычислить ориентацию всех идентифицированных плоскостей, а также получить обширную информацию о снимаемой сцене с точностью до масштабного коэффициента.