Стерео системы
В предыдущих заметках мы рассмотрели, как с помощью ключевых точек можно значительно улучшить наше понимание -сцены. Мы сосредоточились на настройке эполярной геометрии, чтобы связать точки одной плоскости изображения с точками другой без извлечения какой-либо информации о трёхмерной сцене. В этой заметке мы обсудим, как восстановить информацию о трёхмерной сцене из нескольких двумерных изображений.
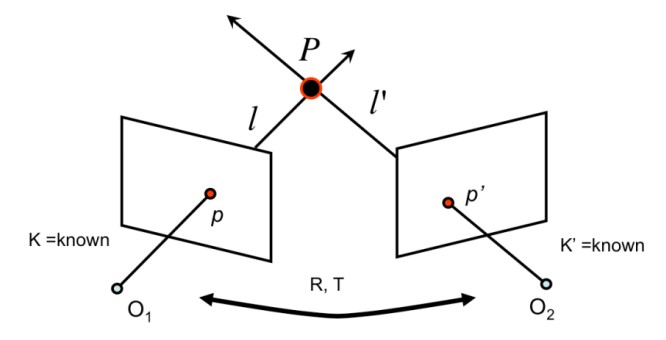
Рисунок 1: Триангуляция точки Р по двум изображениям
Одной из фундаментальных задач в геометрии множественных видов является задача триангуляции — процесс определения местоположения трёхмерной точки по её проекциям на два или более изображений. В задаче триангуляции с двумя видами у нас есть две камеры с известными внутренними параметрами камеры $K$ и $K'$ соответственно. Нам также известны относительные ориентации и смещения $R$, $T$ этих камер относительно друг друга.
Предположим, что у нас есть точка $P$ в трёхмерном пространстве, которая может быть найдена на изображениях двух камер в точках $p$ и $p'$ соответственно. Хотя местоположение $P$ в данный момент неизвестно, мы можем измерить точные местоположения $p$ и $p'$ на изображении. Поскольку $K$, $K'$, $R$, $T$ известны, мы можем вычислить две линии визирования $ℓ$ и $ℓ'$, которые определяются центрами камер $O_1$, $O_2$ и местоположениями изображений $p$, $p'$. Следовательно, $P$ может быть вычислена как точка пересечения $ℓ$ и $ℓ'$.
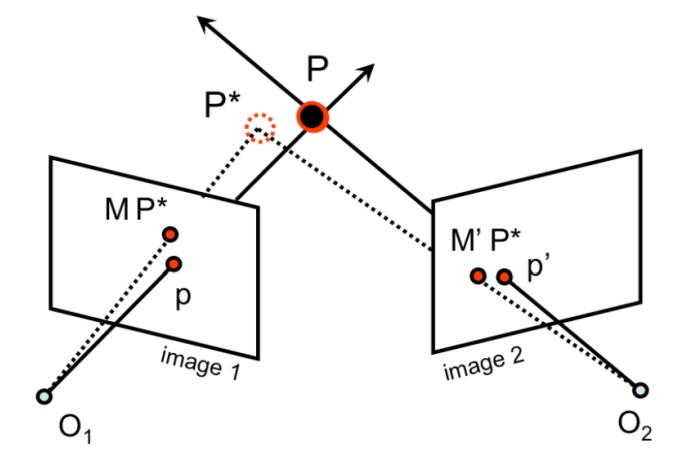
Рисунок 2: Ошибки в проекции точки
Хотя этот процесс кажется простым и математически обоснованным, на практике он работает не очень хорошо. В реальном мире из-за того, что наблюдения $p$ и $p'$ зашумлены, а параметры калибровки камеры не являются точными, поиск точки пересечения прямых $ℓ$ и $ℓ'$ может быть проблематичным. В большинстве случаев она вообще не существует, поскольку эти две прямые могут не пересекаться.
1. Линейный метод триангуляции
В этом разделе мы описываем простой линейный метод триангуляции, который решает проблему отсутствия точки пересечения между лучами. Нам даны две точки на изображениях, которые соответствуют друг другу:
$p = MP = (x, y, 1)$
$p' = M'P = (x', y', 1)$
Вспомним, что векторное произведение двух векторов в трехмерном пространстве дает вектор, перпендикулярный обоим исходным векторам.
В нашем случае: * $p = (x, y, 1)$ — это точка на плоскости изображения * $MP$ — это результат умножения матрицы камеры $M$ на координаты 3D точки $P$
Векторы $p$ и $MP$ коллинеарны (лежат на одной прямой или параллельны), а значит $p \times (MP) = 0$
Развернем это векторное произведение в координатной форме:
$p \times (MP) = \begin{vmatrix} i & j & k \\ x & y & 1 \\ M_1P & M_2P & M_3P \end{vmatrix} = 0$
Раскрывая определитель, получаем:
$p \times (MP) = i(yM_3P - M_2P) - j(xM_3P - M_1P) + k(xM_2P - yM_1P) = 0$
Это векторное равенство равно нулю тогда и только тогда, когда каждая его компонента равна нулю:
$x(M_3P) − (M_1P) = 0$
$y(M_3P) − (M_2P) = 0$
$x(M_2P) − y(M_1P) = 0$ (1)
где $M_i$ — это $i$-я строка матрицы $M$.
Подобные ограничения можно сформулировать для $p'$ и $M'$. Используя ограничения обоих изображений, мы можем сформулировать линейное уравнение вида
$AP = 0$, где
$A = \begin{bmatrix} xM_3 − M_1 \\ yM_3 − M_2 \\ x'M'_3 − M'_1 \\ y'M'_3 − M'_2 \end{bmatrix}$ (2)
Это уравнение можно решить с помощью сингулярного разложения (SVD), чтобы найти наилучшую линейную оценку точки $P$.
Другой интересный аспект этого метода заключается в том, что он фактически может обрабатывать триангуляцию из нескольких видов. Для этого нужно просто добавить дополнительные строки к матрице $A$, соответствующие новым ограничениям от дополнительных видов.
Однако этот метод не подходит для проективной реконструкции.
Основная причина - особенность разложения методом SVD, которое решается при ограничении $∥P∥ = 1$.
Ограничение $|P| = 1$ означает, что вектор $P$ нормирован, то есть его длина равна единице. Однако при проективных преобразованиях это свойство не сохраняется, так как такие преобразования изменяют длины векторов.
Другими словами, сингулярное разложение не является инвариантным относительно проективного преобразования $H$.
Например, предположим, что мы заменяем матрицы камер $M$ и $M'$ на матрицы, подвергнутые проективному преобразованию $MH^{-1}$ и $M'H^{-1}$. Тогда матрица линейных уравнений $A$ становится равной $AH^{-1}$. Следовательно, решение $P$ для предыдущей оценки $AP = 0$ будет соответствовать решению $HP$ для преобразованной задачи $(AH^{-1})(HP) = 0$.
Поэтому линейный метод триангуляции вычислительно простой, но часто не является оптимальным решением задачи триангуляции.
2. Нелинейный метод триангуляции
Вместо этого задача триангуляции для реальных сценариев часто математически характеризуется как решение задачи минимизации:
$\min_{\hat{P}} |M\hat{P} - p|^2 + |M'\hat{P} - p'|^2$ (3)
В приведенном уравнении мы стремимся найти точку $\hat{P}$ в 3D пространстве, которая наилучшим образом аппроксимирует $P$, путем нахождения наилучшей оценки методом наименьших квадратов для ошибки репроекции $\hat{P}$ на обоих изображениях.
Ошибка репроекции для 3D точки на изображении — это расстояние между проекцией этой точки на изображении и соответствующей наблюдаемой точкой в плоскости изображения. В случае нашего примера на рисунке 2, поскольку $M$ — это проективное преобразование из 3D пространства в изображение 1, проецируемая точка $\hat{P}$ на изображении 1 равна $M\hat{P}$. Соответствующее наблюдение точки $\hat{P}$ на изображении 1 — это $p$. Таким образом, ошибка репроекции для точки $P$ на изображении 1 равна расстоянию $|M\hat{P} - p|$.
Общая ошибка репроекции, найденная в уравнении (3), представляет собой сумму ошибок репроекции для всех точек на изображении. В случае более чем двух изображений мы просто добавим дополнительные члены расстояния в целевую функцию:
$\min_{\hat{P}} \sum_i |M\hat{P}_i - p_i|^2$ (4)
На практике существует множество очень сложных методов оптимизации, которые дают хорошие приближения к решению задачи. Однако в рамках курса мы сосредоточимся только на одном из этих методов — алгоритме Гаусса-Ньютона для нелинейных наименьших квадратов.
Общая задача нелинейных наименьших квадратов заключается в нахождении $x \in \mathbb{R}^n$, который минимизирует:
$|r(x)|^2 = \sum_{i=1}^m r_i(x)^2$ (5)
где $r$ — любая остаточная функция $r: \mathbb{R}^n \rightarrow \mathbb{R}^m$ такая, что $r(x) = f(x) - y$ для некоторой функции $f$, входных данных $x$ и наблюдения $y$. Задача нелинейных наименьших квадратов сводится к обычной линейной задаче наименьших квадратов, когда функция $f$ линейна. Однако помните, что в общем случае наши матрицы камер не являются аффинными.
Если мы обозначим $e_i$ как вектор $2 \times 1$, $e_i = M\hat{P}_i - p_i$, то мы можем переформулировать нашу задачу оптимизации следующим образом:
$\min_{\hat{P}} \sum_i e_i(\hat{P})^2$ (6)
что может быть идеально представлено как задача нелинейных наименьших квадратов.
В этих заметках мы рассмотрим, как можно использовать популярный алгоритм Гаусса-Ньютона для нахождения приближенного решения этой задачи нелинейных наименьших квадратов. Сначала предположим, что у нас есть достаточно разумная оценка 3D точки $\hat{P}$, которую мы можем вычислить с помощью предыдущего линейного метода.
Ключевая идея алгоритма Гаусса-Ньютона заключается в обновлении нашей оценки путем корректировки её в направлении еще лучшей оценки, которая минимизирует ошибку репроекции. На каждом шаге мы хотим обновить нашу оценку $\hat{P}$ на некоторую величину $\delta P$: $\hat{P} = \hat{P} + \delta P$.
Как выбрать параметр обновления δP? Ключевая идея алгоритма Гаусса-Ньютона заключается в линеаризации остаточной функции вблизи текущей оценки $\hat{P}$. В нашем случае это означает, что остаточная ошибка $e$ точки $P$ может быть представлена как:
$e(\hat{P} + \delta P) \approx e(\hat{P}) + \frac{\partial e}{\partial P} \delta P$ (7)
После этого задача минимизации преобразуется в:
$\min_{\delta P} \left| \frac{\partial e}{\partial P} \delta P - (-e(\hat{P})) \right|^2$ (8)
Когда мы формулируем остаточную функцию таким образом, становится видно, что она принимает формат стандартной задачи линейных наименьших квадратов. Для задачи триангуляции с $N$ изображениями решение линейных наименьших квадратов имеет вид:
$\delta P = -(J^TJ)^{-1}J^Te$ (9)
где:
$e = \begin{bmatrix} e_1 \\ \vdots \\ e_N \end{bmatrix} = \begin{bmatrix} p_1 - M_1\hat{P} \\ \vdots \\ p_n - M_n\hat{P} \end{bmatrix}$ (10)
и
$J = \begin{bmatrix} \frac{\partial e_1}{\partial \hat{P}_1} & \frac{\partial e_1}{\partial \hat{P}_2} & \frac{\partial e_1}{\partial \hat{P}_3} \\ \vdots & \vdots & \vdots \\ \frac{\partial e_N}{\partial \hat{P}_1} & \frac{\partial e_N}{\partial \hat{P}_2} & \frac{\partial e_N}{\partial \hat{P}_3} \end{bmatrix}$ (11)
Важно отметить, что вектор остаточной ошибки для конкретного изображения $e_i$ является вектором размера $2 \times 1$, поскольку в плоскости изображения есть два измерения. Следовательно, в простейшем случае с двумя камерами ($N = 2$) вектор остаточной ошибки $e$ будет иметь размер $2N \times 1 = 4 \times 1$, а матрица Якоби $J$ — размер $2N \times 3 = 4 \times 3$.
Этот метод легко обрабатывает множественные виды, так как дополнительные изображения учитываются путем добавления соответствующих строк к вектору $e$ и матрице $J$. После вычисления обновления $\delta P$ мы можем просто повторить процесс фиксированное количество шагов или до численной сходимости.
Важное свойство алгоритма Гаусса-Ньютона заключается в том, что наше предположение о линейности остаточной функции вблизи оценки не гарантирует сходимость. Поэтому на практике всегда полезно установить верхнюю границу количества обновлений оценки.
Резюме
Триангуляция представляет собой фундаментальный процесс определения местоположения трёхмерной точки по её проекциям на два или более изображений. В основе этого метода лежит работа с двумя камерами, для которых известны внутренние параметры $K$ и $K'$, а также их относительные ориентации и смещения $R$ и $T$.
При наличии трёхмерной точки $P$, которая проецируется на изображения в точках $p$ и $p'$, задача сводится к вычислению линий визирования $\ell$ и $\ell'$, определяемых центрами камер $O_1$ и $O_2$. В идеальном случае точка $P$ находится в точке пересечения этих линий. Однако на практике из-за шума в измерениях и неточностей калибровки камер точное пересечение линий может отсутствовать.
Существует два основных подхода к решению задачи триангуляции.
Линейный метод основан на использовании векторного произведения для формирования системы линейных уравнений вида $AP = 0$, которая решается с помощью сингулярного разложения (SVD). Несмотря на вычислительную простоту, этот метод имеет существенные ограничения, главным из которых является невозможность корректной работы с проективными преобразованиями.
Более эффективным является нелинейный метод триангуляции, который формулирует задачу как минимизацию ошибки репроекции. Основная идея заключается в поиске такой трёхмерной точки $\hat{P}$, которая обеспечивает минимальное расстояние между её проекциями на изображения и наблюдаемыми точками.
Для решения этой оптимизационной задачи широко применяется алгоритм Гаусса-Ньютона. Метод работает путём итеративного обновления оценки точки через вычисление остаточной ошибки $e$ и матрицы Якоби $J$. На каждом шаге происходит корректировка оценки по формуле:
$\delta P = -(J^TJ)^{-1}J^Te$
Важным преимуществом нелинейного подхода является его способность работать с множественными видами — дополнительные изображения просто добавляются в систему уравнений. При этом алгоритм обеспечивает более точную оценку положения точки за счёт минимизации суммарной ошибки репроекции на всех изображениях.
Несмотря на эффективность, метод требует разумной начальной оценки и контроля количества итераций для обеспечения сходимости. Тем не менее, нелинейная триангуляция остаётся предпочтительным выбором для практических приложений, где требуется высокая точность реконструкции трёхмерных сцен.