Извлечение структуры сцены из движения камеры
1. Аффинная структура из движения
В конце предыдущего раздела мы затронули интересную тему, как можно использовать более двух проекций сцены, чтобы получить информацию о трёхмерной сцене. Теперь давайте более подробно рассмотрим расширение геометрии двух камер на более общий случай множества камер. Комбинируя наблюдения точек из нескольких видов, мы сможем одновременно определить как трёхмерную структуру сцены, так и параметры камеры — эта задача известна как структура из движения (structure from motion).
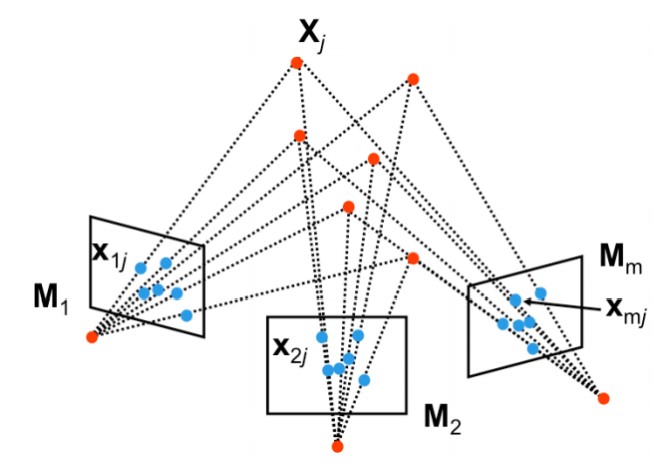
Рисунок 1: Общая схема структуры из движения
Схема для формальной постановки задачи приведена на рисунке 1. Предположим, что у нас есть $m$ камер с матрицами камер $M_i$, которые кодируют как внутренние, так и внешние параметры камер. Пусть $X_j$ — одна из $n$ трёхмерных точек в сцене. Каждая трёхмерная точка может быть видна в нескольких камерах в позиции $x_{ij}$, которая является проекцией $X_j$ на изображение камеры $i$ с помощью проективного преобразования $M_i$.
Цель оценки структуры из движения - восстановление как структуры сцены (то есть $n$ трёхмерных точек $X_j$), так и движения камер (то есть $m$ проективных матриц $M_i$) из всех наблюдений $x_{ij}$.
Основные данные этой системы включают в себя:
- Структура сцены: набор трёхмерных точек $X_j$, которые составляют геометрию сцены.
- Движение камер: параметры проективных матриц $M_i$, описывающие положение и ориентацию каждой камеры.
- Наблюдения: множество проекций $x_{ij}$, показывающих, где трёхмерные точки видны на изображениях разных камер.
Таким образом, задача структуры из движения заключается в одновременном восстановлении трёхмерной геометрии сцены и параметров движения камер на основе множества двумерных наблюдений. Это фундаментальная задача в компьютерном зрении и трёхмерной реконструкции.
Прежде чем решать общую задачу структуры из движения, мы начнем с более простой задачи, которая предполагает, что камеры являются аффинными или слабоперспективными. В конечном итоге отсутствие операции перспективного масштабирования упрощает математическое выведение для этой задачи.
Ранее мы вывели приведенные уравнения для случаев перспективы и слабой перспективы. Вспомним, что в полной перспективной модели матрица камеры определяется как:
$M = \begin{bmatrix} A & b \\ v & 1 \end{bmatrix}$ (1)
где $v$ — некоторый ненулевой вектор размером $1 \times 3$. С другой стороны, для модели слабой перспективы $v = 0$. Мы обнаруживаем, что это свойство делает однородную координату $MX$ равной 1:
$x = MX = \begin{bmatrix} m_1 \\ m_2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ 1 \end{bmatrix} = \begin{bmatrix} m_1X \\ m_2X \\ 1 \end{bmatrix}$ (2)
Следовательно, при переходе от однородных к евклидовым координатам нелинейность проективного преобразования исчезает, и преобразование слабой перспективы действует как простой увеличитель. Мы можем представить проекцию в более компактной форме:
$ M_{affine} = \begin{bmatrix} m_1X \\ m_2X \end{bmatrix} = [A \ b]X = AX + b$ (3)
Таким образом, теперь мы используем аффинную модель камеры для выражения связи между точкой $X_j$ в 3D и соответствующими наблюдениями в каждой аффинной камере (например, $x_{ij}$ в камере $i$).
Возвращаясь к задаче структуры из движения, нам нужно оценить $m$ матриц $M_i$ и $n$ векторов мировых координат $X_j$. Такая система содержит всего $8m + 3n$ неизвестных, на основе $mn$ наблюдений. Каждое наблюдение создает 2 ограничения на камеру, поэтому имеется $2mn$ уравнений с $8m + 3n$ неизвестными.
Мы можем использовать это уравнение, чтобы определить нижнюю границу количества соответствующих наблюдений в каждом из изображений, которые нам необходимы. Например, если у нас есть $m = 2$ камеры, то нам нужно иметь как минимум $n = 16$ точек в 3D. Однако как решить эту задачу, когда у нас достаточно соответствующих точек, помеченных на каждом изображении?
2 Метод факторизации Томаси и Канеде
В этой части мы рассмотрим метод факторизации Томаси и Канеде для решения задачи аффинной структуры из движения. Этот метод состоит из двух основных этапов: центрирования данных и собственно факторизации.
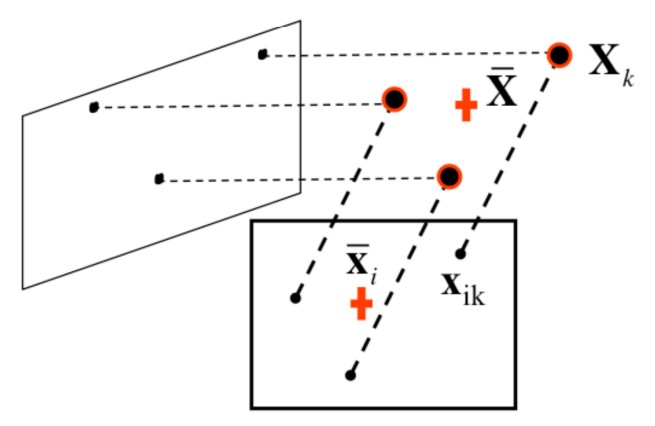
Рисунок 2: Центроид наблюдаемых точек
На рисунке 2 приведен пример центрирования - все точки изображения размещаются таким образом, чтобы их центроид находился в начале координат в плоскости изображения. Аналогично мы размещаем систему мировых координат так, чтобы начало координат находилось в центроиде 3D точек. Основная идея этого этапа — центрирование данных в начале координат. Для этого для каждого изображения $i$ мы переопределяем новые координаты $\hat{x}{ij}$ для каждой точки изображения $x_i$:}$, вычитая их центроид $\bar{x
$\hat{x}{ij} = x} - \bar{xi = x$ (4)} - \frac{1}{n} \sum_{j=1}^{n} x_{ij
Напомним, что задача аффинной структуры из движения позволяет нам определить взаимосвязь между точками изображения $x_{ij}$, переменными матрицы камеры $A_i$ и $b_i$, и 3D точками $X_j$ как:
$x_{ij} = A_i X_j + b_i$ (5)
После этапа центрирования мы можем объединить определение центрированных точек изображения $\hat{x}_{ij}$ из уравнения (4) и аффинное выражение из уравнения (5):
$\hat{x}{ij} = x = $} - \frac{1}{n} \sum_{k=1}^{n} x_{ik
$= A_i X_j - \frac{1}{n} \sum_{k=1}^{n} A_i X_k = A_i(X_j - \frac{1}{n} \sum_{k=1}^{n} X_k) = $
$ = A_i(X_j - \bar{X}) = A_i \hat{X}_j$ (6)
Как видно из уравнения (6), если мы переместим начало системы мировых координат в центроид $\bar{X}$, то центрированные координаты точек изображения $\hat{x}_{ij}$ и центрированные координаты 3D точек $\hat{X}_j$ связаны только одной матрицей $2 \times 3$ $A_i$. В конечном итоге этап центрирования метода факторизации позволяет нам создать компактное матричное произведение для связи 3D структуры с наблюдаемыми точками на множестве изображений.
Однако заметим, что в матричном произведении $\hat{x}{ij} = A_i \hat{X}_j$ у нас есть доступ только к значениям в левой части уравнения. Таким образом, нам нужно каким-то образом выделить матрицы движения $A_i$ и структуру $X_j$. Используя все наблюдения для всех камер, мы можем построить матрицу измерений $D$, состоящую из $n$ наблюдений в $m$ камерах (помните, что каждая запись $\hat{x}$ — это вектор $2 \times 1$):
$D = \begin{bmatrix} \hat{x}{11} & \hat{x}} & \dots & \hat{x{1n} \\ \hat{x}} & \hat{x{22} & \dots & \hat{x}} \\ \vdots & \vdots & \ddots & \vdots \\ \hat{x{m1} & \hat{x}$ (7)} & \dots & \hat{x}_{mn} \end{bmatrix
Теперь вспомним, что из-за нашего аффинного предположения, $D$ может быть выражена как произведение матрицы движения $2m \times 3$ $M$ (которая включает матрицы камер $A_1, \dots, A_m$) и матрицы структуры $3 \times n$ $S$ (которая включает 3D точки $X_1, \dots, X_n$). Важный факт, который мы будем использовать, заключается в том, что $rank(D) = 3$, поскольку $D$ — это произведение двух матриц, максимальное измерение которых равно 3.
Чтобы разложить $D$ на $M$ и $S$, мы будем использовать сингулярное разложение:
$D = U\Sigma V^T = \begin{bmatrix} u_1 & \dots & u_n \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & 0 & 0 & \dots & 0 \\ 0 & \sigma_2 & 0 & 0 & \dots & 0 \\ 0 & 0 & \sigma_3 & 0 & \dots & 0 \\ 0 & 0 & 0 & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \dots & 0 \end{bmatrix} \begin{bmatrix} v_1^T \\ \vdots \\ v_n^T \end{bmatrix} = $
$ = \begin{bmatrix} u_1 & u_2 & u_3 \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \begin{bmatrix} v_1^T \\ v_2^T \\ v_3^T \end{bmatrix} = U_3\Sigma_3V_3^T$ (8)
В этом разложении $\Sigma_3$ определяется как диагональная матрица, образованная ненулевыми сингулярными значениями, в то время как $U_3$ и $V_3^T$ получаются путем взятия соответствующих трех столбцов матрицы $U$ и строк матрицы $V^T$ соответственно.
К сожалению, на практике $rank(D) > 3$ из-за шума измерений и аффинного приближения камеры. Однако мы помним замечательное свойство сингулярного разложения, что когда $rank(D) > 3$, $U_3W_3V_3^T$ все еще остается наилучшим возможным приближением ранга 3 для $MS$ в смысле нормы Фробениуса.
При внимательном рассмотрении мы видим, что матричное произведение $\Sigma_3V_3^T$ образует матрицу размером $3 \times n$, что точно соответствует размеру матрицы структуры $S$. Аналогично, $U_3$ — это матрица размером $2m \times 3$, что соответствует размеру матрицы движения $M$.
Хотя такой способ сопоставления компонентов SVD-разложения с $M$ и $S$ приводит к физически и геометрически правдоподобному решению задачи аффинной структуры из движения, этот выбор не является единственным решением. Например, мы также могли бы установить матрицу движения как $M = U_3\Sigma_3$, а матрицу структуры как $S = V_3^T$, поскольку в обоих случаях матрица наблюдений $D$ остается той же.
Так какое разложение выбрать? В своей работе Томаси и Канеде пришли к выводу, что наиболее надежным выбором факторизации является $M = U_3\sqrt{\Sigma_3}$ и $S = \sqrt{\Sigma_3}V_3^T$.
Тем не менее, мы обнаруживаем внутреннюю неоднозначность в любом выборе факторизации $D = MS$, поскольку в разложение можно вставить любую произвольную обратимую матрицу $3 \times 3$ $A$:
$D = MA A^{-1}S = (MA)(A^{-1}S)$ (9)
Это означает, что матрицы камер, полученные из движения $M$, и 3D точки, полученные из структуры $S$, определяются с точностью до умножения на общую матрицу $A$. Следовательно, наше решение недоопределено и требует дополнительных ограничений для разрешения этой аффинной неоднозначности. Несмотря на то, что параллельность линий сохраняется, метрический масштаб элементов матрицы и координат точек остаются неизвестными.
Другой важный класс неоднозначностей для реконструкции — это неоднозначность подобия, которая возникает, когда реконструкция верна с точностью до преобразования подобия (вращение, перенос и масштабирование). Реконструкция только с неоднозначностью подобия известна как метрическая реконструкция. Эта неоднозначность существует даже при внутренней калибровке камер. Хорошая новость заключается в том, что для откалиброванных камер неоднозначность подобия является единственной возможной неоднозначностью.
Тот факт, что невозможно восстановить абсолютный масштаб сцены по изображениям, довольно интуитивен. Масштаб объекта, абсолютное положение и каноническая ориентация всегда будут неизвестны, если мы не сделаем дополнительные предположения (например, знаем высоту дома на рисунке) или не включим дополнительные данные о матрице переноса. Это происходит потому, что одни атрибуты могут компенсировать другие. Например, чтобы получить то же изображение, мы можем просто отодвинуть объект назад и соответствующим образом масштабировать его.
Один из примеров устранения неоднозначности подобия возник во время процедуры калибровки камеры, когда мы сделали предположение, что знаем расположение калибровочных точек относительно мировой системы координат. Это позволило нам узнать размер квадратов шахматной доски для определения метрического масштаба 3D структуры.
3. Структура из движения с перспективными преобразованиями камер (метод разложения)
После изучения упрощённой задачи аффинной структуры из движения давайте рассмотрим общий случай для проективных камер $M_i$.
В общем случае с проективными камерами каждая матрица камеры $M_i$ содержит 11 степеней свободы, поскольку она определена с точностью до масштабного множителя:
$M_i = \begin{bmatrix} a_{11} & a_{12} & a_{13} & b_1 \\ a_{21} & a_{22} & a_{23} & b_2 \\ a_{31} & a_{32} & a_{33} & 1 \end{bmatrix}$ (10)
Более того, в общем случае решения определение матриц структуры из движения могут быть определены с точностью до проективного преобразования, как и при афинной неоднозначности. Мы всегда можем произвольно применить проективное преобразование $4 \times 4$ $H$ к матрице движения, при условии, что мы также преобразуем матрицу структуры с помощью обратного преобразования $H^{-1}$. Результирующие наблюдения в плоскости изображения останутся прежними.
Аналогично аффинному случаю, мы можем сформулировать общую задачу структуры из движения как оценку как $m$ матриц движения $M_i$, так и $n$ 3D точек $X_j$ на основе $mn$ наблюдений $x_{ij}$. Поскольку камеры и точки могут быть восстановлены только с точностью до проективного преобразования $4 \times 4$ с учётом масштаба (15 параметров), у нас есть $11m + 3n - 15$ неизвестных в $2mn$ уравнениях.
Из этих фактов мы можем определить необходимое количество видов и наблюдений, требуемых для решения неизвестных.
4. Алгебраический подход к SFM с перспективой
Теперь рассмотрим алгебраический подход, который использует концепцию фундаментальной матрицы $F$ для решения задачи оценки структуры из движения для двух камер. В отличии от метода разложения, в алгебраическом подходе мы рассматриваем последовательные пары камер для определения матриц камер $M_1$ и $M_2$ с точностью до перспективного преобразования. Затем мы находим перспективное преобразование $H$ такое, что $M_1H = [I \ 0]$ и $M_2H = [A \ B]$.
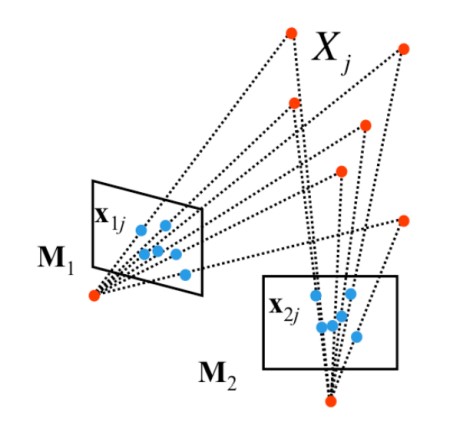
Как показано на рисунке 3, основная идея алгебраического подхода заключается в вычислении двух матриц камер $M_1$ и $M_2$, которые могут быть вычислены только с точностью до перспективного преобразования $H$.
Поскольку каждая $M_i$ может быть вычислена только с точностью до перспективного преобразования $H$, мы всегда можем рассмотреть такое $H$, при котором матрица проекции первой камеры $M_1H^{-1}$ будет канонической. Разумеется, то же преобразование должно быть применено и ко второй камере, что приводит к следующей форме:
$M_1H^{-1} = [I \ 0]$
$M_2H^{-1} = [A \ b]$ (11)
Для выполнения этой задачи сначала необходимо вычислить фундаментальную матрицу $F$ с помощью алгоритма восьми точек. Далее матрица $F$ используется для оценки проективных матриц камер $M_1$ и $M_2$.
Для этой оценки определим 3D точку $P$ и соответствующие наблюдения на изображениях $p$ и $p'$.
Поскольку мы применили $H^{-1}$ к обеим матрицам проекции камер, мы также должны применить $H$ к структуре, получая $P_e = HP$.
Таким образом, мы можем связать координаты пикселей $p$ и $p'$ с преобразованной структурой следующим образом:
$p = M_1P = M_1H^{-1}HP = [I \ 0]P_e$
$p' = M_2P = M_2H^{-1}HP = [A \ b]P_e$ (12)
Интересное свойство между двумя соответствиями изображений $p$ и $p'$ возникает при подстановках:
$p' = [A \ b] P_e =$
$= A[I \ 0] P_e + b =$
$= Ap + b$ (13)
Используя уравнение (13), мы можем записать векторное произведение между $p'$ и $b$ как:
$p' \times b = (Ap + b) \times b = Ap \times b$ (14)
По определению векторного произведения, $p' \times b$ перпендикулярен $p'$. Поэтому мы можем записать:
$0 = p'^T(p' \times b) = p'^T(Ap \times b) = p'^T \cdot (b \times Ap) = p'^T[b\times] Ap$ (15)
Рассматрев это ограничение более внимательно, можно увидеть, что оно напоминает общее определение фундаментальной матрицы
$p'^TFp = 0$
Если мы установим $F = [b\times] A$, то извлечение $A$ и $b$ снова сводится к задаче разложения.
Давайте начнем с определения $b$. Снова используя определение векторного произведения, мы можем записать:
$F^\top b = [[b\times] A]^\top b = 0$ (16)
Поскольку матрица $F$ является сингулярной, вектор $b$ можно вычислить как решение методом наименьших квадратов уравнения $F^\top b = 0$ при условии $|b| = 1$ с помощью сингулярного разложения (SVD).
Как только вектор $b$ становится известным, мы можем вычислить матрицу $A$. Если мы положим $A = −[b\times] F$, то можем проверить, что это определение удовлетворяет условию $F = [b\times] A$:
$[b\times] A' = −[b\times][b\times] F$ $= (bb^\top − |b|^2I)F$ $= bb^\top F + |b|^2F$ $= 0 + 1 · F$ $= F$ (17)
Следовательно, мы определяем два выражения для матриц наших камер $M_1H^{−1}$ и $M_2H^{−1}$:
$\tilde{M}_1 = [I \ 0]$ $\tilde{M}_2 = [−[b\times] F \ b]$ (18)
Прежде чем завершить этот раздел, мы хотим дать геометрическую интерпретацию для вектора $b$. Мы знаем, что $b$ удовлетворяет условию $Fb = 0$. Вспомним эпиполярные ограничения, которые мы вывели в предыдущих конспектах, где было показано, что эпиполы на изображении — это точки, которые отображаются в ноль при преобразовании фундаментальной матрицей (то есть $Fe_2 = 0$ и $F^\top e_1 = 0$). Таким образом, мы видим, что $b$ является эпиполом. Это даёт нам новый набор уравнений для матриц проекции камер (формулы 4.10):
$\tilde{M}_1 = [I \ 0]$ $\tilde{M}_2 = [−[e\times] F \ e]$ (19)