Введение

В классическом стереовидении мы пытаемся определить положение трёхмерной точки в пространстве, используя соответствующие точки на двух изображениях. Главная сложность здесь — решить проблему соответствия: как понять, что точка на одном изображении соответствует точке на другом?

Эта проблема усложняется тем, что в сцене присутствует множество трёхмерных точек, и нам нужно обработать их все. Сегодня мы рассмотрим альтернативный подход к реконструкции трехмерной сцены.

1. Активное стерео

Чтобы решить проблему поиска соответствующих точек, была разработана концепция активного стерео. Её суть состоит в том, что вместо одной из камер используется специальный проектор, который взаимодействует с трёхмерной сценой. Проектор создаёт на объекте специальный узор или проецирует определённую точку, а вторая камера наблюдает за тем, как этот узор отображается на объекте. Поскольку мы точно знаем, что и куда проецируем (положение точки, цвет, яркость), нам легко найти соответствующую точку на изображении второй камеры

Главное преимущество активного стерео состоит в том, что оно значительно упрощает решение проблему поиска соответствующих точек. Проектор и камера работают как единая система, создавая особую геометрию, похожую на обычную стереосистему, но с виртуальной проекционной плоскостью вместо второй камеры.

Этот метод особенно эффективен, когда нужно точно определить положение объектов в пространстве, так как мы контролируем проецируемый узор и можем легко отследить его отображение на второй камере.

Рисунок 1: Система активного стерео

На рисунке 1 показано, как проектор используется для проецирования точки $p$ из виртуальной плоскости на объект в трёхмерном пространстве, создавая точку в трёхмерном пространстве $P$. Эта трёхмерная точка $P$ должна наблюдаться второй камерой как точка $p'$.

Поскольку мы знаем, что именно проецируем (например, положение точки $p$ в виртуальной плоскости, цвет и интенсивность проекции и так далее), мы можем легко обнаружить соответствующее наблюдение во второй камере $p'$.

Распространённый прием в активном стерео — проецировать из виртуальной плоскости вертикальную полосу $s$ вместо одиночной точки. Этот случай очень похож на случай с точкой, когда линия $s$ проецируется в виде полосы в трёхмерное пространство $S$ и наблюдается камерой как линия $s'$.

Рисунок 2: Проецирование отрезка

Если проектор и камера расположены параллельно или откалиброваны, мы можем легко обнаружить соответствующие точки, просто пересекая $s'$ с горизонтальными эпиполярными линиями. На основе этих соответствий мы можем использовать методы триангуляции, рассмотренных в предыдущих материалах курса, чтобы восстановить все трёхмерные точки на полосе $S$.

Перемещая линию по сцене и повторяя процесс, мы можем восстановить полную форму всех видимых объектов в сцене.

Обратите внимание, что одно из требований для работы этого алгоритма заключается в том, что проектор и камера должны быть откалиброваны. Активная стереосистема может быть откалибрована с использованием аналогичных техник, как описано в предыдущих заметках.

Сначала мы калибруем камеру с помощью калибровочного устройства. Затем, проецируя известные полосы на калибровочное устройство и используя соответствующие наблюдения в недавно откалиброванной камере, мы можем установить ограничения для оценки внутренних и внешних параметров проектора.

После калибровки эта активная стереоустановка может давать очень точные результаты. В 2000 году Марк Левой и его студенты из Стэнфорда продемонстрировали, что, используя точно настроенный лазерный сканер, они могли восстановить форму скульптуры «Пьета» Микеланджело с субмиллиметровой точностью.

Однако в некоторых случаях наличие точно настроенного проектора может быть слишком дорогим или неудобным. Альтернативный подход, который использует гораздо более дешёвую установку, использует тени для создания активных паттернов на объекте, который мы хотим восстановить.

Размещая палочку между объектом и источником света в известном положении, мы можем эффективно проецировать полосу на объект, как и раньше. Перемещение палочки позволяет нам проецировать различные теневые полосы на объект и восстанавливать объект аналогичным образом, как и раньше.

Этот метод, хотя и намного дешевле, имеет тенденцию давать менее точные результаты, поскольку требует очень хорошей калибровки между палочкой, камерой и источником света, при этом необходимо поддерживать компромисс между длиной и тонкостью тени палочки.

Одно из ограничений проецирования единственной полосы на объекты заключается в том, что этот метод довольно медленный, поскольку проектору необходимо охватить весь объект с разных ракурсов. Более того, это означает, что данный метод не может фиксировать деформации в режиме реального времени.

Естественное развитие этой идеи — попытка восстановить объект путём проецирования одного кадра или изображения вместо последовательного сканирования. Суть заключается в проецировании известного узора из различных полос на весь видимый участок объекта, а не одной полосы.

Цвета этих полос разработаны таким образом, чтобы их можно было однозначно идентифицировать на изображении. Рисунок 3 иллюстрирует этот метод с использованием множества цветных полос. Эта концепция легла в основу многих современных датчиков глубины, например, оригинальной версии Microsoft Kinect.

На практике такие датчики используют инфракрасные лазерные проекторы, которые позволяют захватывать трёхмерные видеоданные при любых условиях внешней освещённости.

### 2. Методы объёмного стереовидения

Альтернативой как традиционному стереовидению, так и активному стерео является объёмное стереовидение, которое переворачивает проблему использования соответствующих точек для восстановления трёхмерной структуры.

Рисунок 4: Основная идея объемного стереовидения - поиск точки в известном объеме

В объёмном стереовидении мы предполагаем, что трёхмерная точка, которую мы пытаемся оценить, находится в некотором ограниченном, известном объёме. Затем мы проецируем гипотетическую трёхмерную точку обратно в откалиброванные камеры и проверяем, согласуются ли эти проекции в нескольких видах. Рисунок 4 иллюстрирует общую схему задачи объёмного стереовидения.

Поскольку мы предполагаем, что точки, которые мы хотим восстановить, содержатся в ограниченном объёме, этот метод пригоден для восстановления трёхмерных моделей конкретных объектов. Это главное отличие от более общей задачи восстановления моделей сцены, в которой расположение объектов может быть неограниченным.

Основной принцип любого метода объёмного стереовидения заключается в том, чтобы сначала определить способ для определения согласованности точки, которая проецируется на несколько ракурсов изображений. Известно множество различных методов определения того, что мы будем считать согласованными наблюдениями. Мы кратко опишем три основных метода:
- пространственное вырезание (Space carving),
- теневое вырезание (shadow carving),
- раскраска вокселей (voxel coloring).

2.1 Space carving

Идея пространственного вырезания (space carving) в основном основана на наблюдении, что контуры объекта предоставляют богатый источник геометрической информации об этом объекте.

Рисунок 5: Силуэт объекта и визуальный конус

В контексте множественных видов сначала рассмотрим задачу, проиллюстрированную на рисунке 5. Каждая камера наблюдает некоторую видимую часть объекта, по которой можно определить контур. При проецировании в плоскость изображения этот контур охватывает набор пикселей, известный как силуэт объекта в плоскости изображения. Пространственное вырезание в конечном итоге использует силуэты объектов с разных видов для обеспечения согласованности.

Однако если у нас нет информации о трёхмерной сцене, а есть только её изображения, то как мы можем получить информацию о силуэтах? К счастью, одно из практических преимуществ работы с силуэтами заключается в том, что их можно легко обнаружить на изображениях, если мы контролируем фон за объектом, который хотим восстановить. Например, мы можем использовать «зелёный экран» за объектом или использовать специальные алгоритмы отделения объекта от фона.

Теперь, когда у нас есть силуэты, как мы можем их использовать? Напомним, что в объёмном стереовидении у нас есть оценка некоторого объёма, в котором, как мы гарантируем, может находиться объект. Теперь введём понятие визуального конуса — это охватывающая поверхность, определяемая центром камеры и контуром объекта в плоскости изображения. По построению сцены гарантируется, что объект будет полностью находиться как в начальном объёме, так и в визуальном конусе.

Рисунок 6: Построение визуальной оболочки

Если у нас есть множество видов с разных ракурсов, мы можем вычислить визуальные конусы для каждого вида. Поскольку, по определению, объект находится в каждом из этих визуальных конусов, он должен лежать в их пересечении, как показано на рисунке 6. Такое пересечение часто называют визуальной оболочкой (visual hull).

На практике мы сначала начинаем с определения рабочего объёма, в котором, как мы знаем, находится объект. Например, если наши камеры окружают объект, мы можем просто сказать, что рабочий объём — это всё внутреннее пространство, ограниченное камерами. Мы разделяем этот объём на маленькие единицы, известные как воксели, создавая то, что называется воксельной сеткой. Мы берём каждый воксель из воксельной сетки и проецируем его на каждый из видов. Если воксель не содержится в силуэте на каком-либо виде, он отбрасывается. Следовательно, в конце алгоритма пространственного вырезания у нас остаются воксели, содержащиеся внутри визуальной оболочки.

Хотя метод пространственного вырезания позволяет избежать проблемы соответствий и является относительно простым, у него всё ещё есть множество ограничений. Одно из ограничений пространственного вырезания заключается в том, что он масштабируется линейно с количеством вокселей в сетке. По мере уменьшения размера каждого вокселя, количество вокселей в сетке увеличивается кубически. Поэтому получение более точных результатов реконструкции приводит к значительному увеличению времени обработки. Однако некоторые методы, такие как использование октетных деревьев (octrees), могут помочь решить эту проблему. Продвинутые методы включают выполнение итеративной адаптации для уменьшения размера начальной воксельной сетки в тех областях изображений, где это необходимо.

На рисунке 7 показан результат пространственного вырезания при работе с воксельной сеткой. Область представляет собой реконструированный объект после вырезания с использованием двух видов, в то время как затенённая часть внутри — это фактический объект.

Ограничение метода заключается в том, что эффективность пространственного вырезания зависит от количества видов, точности силуэта и даже формы объекта, который мы пытаемся восстановить. Если количество видов слишком мало, мы получаем очень приблизительную оценку визуальной оболочки объекта. По мере увеличения количества видов можно удалить больше лишних вокселей с помощью проверки согласованности.

Кроме того, достоверность проверки согласованности поддерживается только тем фактом, что мы считаем силуэты правильными и гладкими. Если силуэт слишком сложен и содержит больше пикселей, чем мы имеем в распоряжении, наша реконструкция может оказаться неточной. В потенциально ещё худшем случае силуэт пропускает части фактического объекта, что приводит к чрезмерному вырезанию при реконструкции.

Наконец, основным недостатком пространственного вырезания является то, что оно не способно моделировать определённые вогнутости объекта, как показано на рисунке 8.

Рисунок 8: Недостаток пространственного вырезания при наличии вогнутостей на объекте

2.2 Shadow carving

Чтобы обойти проблему вогнутостей, возникающую при пространственном вырезании, нам нужно обратиться к другим формам проверок согласованности.

Одним из важных признаков для определения трёхмерной формы объекта является наличие самотеней — теней, которые объект отбрасывает на себя. Для вогнутых объектов характерно то, что они часто отбрасывают самотени в вогнутых областях.

Рисунок 9: Вырезание с учетом теней

По своей сути теневое вырезание дополняет пространственное вырезание идеей использования самотеней для более точной оценки вогнутостей. Как показано на рисунке 9, общая установка теневого вырезания очень похожа на пространственное вырезание. Объект помещается на поворотный стол, который просматривается откалиброванной камерой. Однако вокруг камеры располагается массив источников света в известных позициях, состояние которых можно соответствующим образом включать и выключать. Эти источники света будут использоваться для того, чтобы заставить объект отбрасывать самотени.

Рисунок 10: Источник света как дополнительный инструмент для построения визуальной оболочки

Как показано на рисунке 10, процесс теневого вырезания начинается с начальной воксельной сетки, которая обрезается с помощью того же подхода, что и при пространственном вырезании. Однако в каждом виде мы можем включать и выключать каждый источник света в массиве, окружающем камеру. Каждый источник света будет создавать различную самотень на объекте. После определения тени в плоскости изображения мы можем найти воксели на поверхности нашей обрезанной воксельной сетки, которые находятся в визуальном конусе тени. Эти поверхностные воксели позволяют нам затем создать новый визуальный конус с источником изображения. Затем мы используем полезный факт, что воксель, являющийся частью обоих визуальных конусов, не может быть частью объекта, чтобы исключить воксели в вогнутости.

Как и в случае с пространственным вырезанием, время работы теневого вырезания зависит от разрешения воксельной сетки. Время работы масштабируется кубически с разрешением воксельной сетки. Однако если имеется N источников света, то теневое вырезание занимает примерно в N + 1 раз больше времени, чем пространственное вырезание, поскольку каждый воксель необходимо проецировать в камеру и на каждый из N источников света.

Подводя итог, теневое вырезание всегда даёт консервативную оценку объёма, которая лучше восстанавливает трёхмерные формы с вогнутостями. Качество результатов зависит как от количества видов, так и от количества источников света. Некоторые недостатки этого подхода заключаются в том, что он не может обрабатывать случаи, когда объект содержит отражающие области или области с низким альбедо. Это связано с тем, что в таких условиях невозможно точно определить тени.

2.3 Раскраска вокселей (Voxel coloring)

И напоследок рассмотрим еще одну технику объёмного стереовидения — раскраска вокселей. Эта техника основана на пространственном вырезании, но для согласованности контуров дополнительно использует согласованность цветов.

Рисунок 11: Раскраска вокселей

Предположим, что нам даны изображения объекта с нескольких точек зрения, который мы хотим восстановить (рисунок 11). Для каждого вокселя мы смотрим на его соответствующие проекции на каждом из изображений и сравниваем цвет каждой из этих проекций. Если цвета этих проекций достаточно совпадают, мы отмечаем воксель как часть объекта.

Одно из преимуществ раскраски вокселей, которого нет в пространственном вырезании, заключается в том, что цвет, связанный с проекциями, может быть перенесён на воксель, что даёт цветную реконструкцию.

В целом существует множество методов, которые можно использовать для проверки согласованности цветов. Один из примеров — установка порога между сходством цветов проекций. Однако существует критическое предположение для любой используемой проверки согласованности цветов: реконструируемый объект должен быть ламбертовским. Это означает, что воспринимаемая яркость любой части объекта не должна меняться с изменением положения точки обзора или позы.

Для неламбертовских объектов, например, сделанных из высокоотражающих материалов, легко представить, что проверка согласованности цветов может дать сбой на вокселях, которые фактически являются частью объекта.

Рисунок 12: Частный случай неоднозначности раскраски вокселей

Одним из недостатков простой раскраски вокселей является то, что она даёт решение, которое не обязательно является уникальным (рисунок 12). Поиск истинного, уникального решения усложняет задачу реконструкции с помощью раскраски вокселей.

Можно устранить неоднозначность в реконструкции, введя ограничение видимости на воксель, которое требует, чтобы воксели проходили в определённом порядке. В частности, мы хотим проходить воксели слой за слоем, начиная с вокселей, расположенных ближе к камерам, а затем переходить к более удалённым вокселям.

При использовании такого порядка мы выполняем проверку согласованности цветов. Затем проверяем, виден ли воксель как минимум двум камерам, что создаёт наше ограничение видимости. Если воксель не виден как минимум двум камерам, он должен быть закрыт и, следовательно, не является частью объекта.

Обратите внимание, что наш порядок обработки ближайших вокселей позволяет нам убедиться, что мы сохраняем воксели, которые могут закрывать более поздние обработанные воксели, чтобы обеспечить это ограничение видимости.

В заключение отметим, что раскраска вокселей имеет преимущество одновременного захвата формы и текстуры объекта. Некоторые из недостатков включают предположение о том, что объект является ламбертовским, и то, что камеры не могут находиться в определённых местах, поскольку воксели должны обрабатываться в определённом порядке из-за ограничения видимости.

Резюме

Мы рассмотрели современные подходы к решению задачи трёхмерной реконструкции объектов, которые позволяют обойти сложности классического стереовидения, связанные с поиском соответствующих точек на разных изображениях.

Основное внимание уделяется двум ключевым направлениям. Первое — активное стерео, где вместо второй камеры применяется специальный проектор, создающий определённые узоры на объекте. Этот метод значительно упрощает определение соответствий между точками. В рамках активного стерео описаны различные техники: от проецирования отдельных точек и полос до создания сложных цветных узоров, подобных тем, что используются в датчиках глубины типа Microsoft Kinect. Также рассматривается вариант с применением теневых проекций, который является более экономичным, хотя и менее точным решением.

Второе направление — объёмное стереовидение, основанное на проверке согласованности проекций точек в ограниченном объёме. Этот подход включает несколько методов реконструкции: пространственное вырезание (space carving), использующее силуэты объекта и воксельные сетки; теневое вырезание (shadow carving), улучшающее реконструкцию вогнутых поверхностей за счёт анализа самотеней; и раскраска вокселей (voxel coloring), позволяющая получать цветные трёхмерные модели благодаря анализу цветовой согласованности.

Описанные методы обладают рядом преимуществ: они существенно упрощают поиск соответствий между точками, обеспечивают возможность создания детальных трёхмерных моделей и могут применяться в различных условиях съёмки. Однако существуют и определённые ограничения: необходимость тщательной калибровки оборудования, требование ламбертовского характера объектов, значительные временные затраты на обработку данных, а также проблемы при работе с отражающими поверхностями.

1. Аффинная структура из движения

В конце предыдущего раздела мы затронули интересную тему, как можно использовать более двух проекций сцены, чтобы получить информацию о трёхмерной сцене. Теперь давайте более подробно рассмотрим расширение геометрии двух камер на более общий случай множества камер. Комбинируя наблюдения точек из нескольких видов, мы сможем одновременно определить как трёхмерную структуру сцены, так и параметры камеры — эта задача известна как структура из движения (structure from motion).

Рисунок 1: Общая схема структуры из движения

Схема для формальной постановки задачи приведена на рисунке 1. Предположим, что у нас есть $m$ камер с матрицами камер $M_i$, которые кодируют как внутренние, так и внешние параметры камер. Пусть $X_j$ — одна из $n$ трёхмерных точек в сцене. Каждая трёхмерная точка может быть видна в нескольких камерах в позиции $x_{ij}$, которая является проекцией $X_j$ на изображение камеры $i$ с помощью проективного преобразования $M_i$.

Цель оценки структуры из движения - восстановление как структуры сцены (то есть $n$ трёхмерных точек $X_j$), так и движения камер (то есть $m$ проективных матриц $M_i$) из всех наблюдений $x_{ij}$.

Основные данные этой системы включают в себя:
- Структура сцены: набор трёхмерных точек $X_j$, которые составляют геометрию сцены.
- Движение камер: параметры проективных матриц $M_i$, описывающие положение и ориентацию каждой камеры.
- Наблюдения: множество проекций $x_{ij}$, показывающих, где трёхмерные точки видны на изображениях разных камер.

Таким образом, задача структуры из движения заключается в одновременном восстановлении трёхмерной геометрии сцены и параметров движения камер на основе множества двумерных наблюдений. Это фундаментальная задача в компьютерном зрении и трёхмерной реконструкции.

Прежде чем решать общую задачу структуры из движения, мы начнем с более простой задачи, которая предполагает, что камеры являются аффинными или слабоперспективными. В конечном итоге отсутствие операции перспективного масштабирования упрощает математическое выведение для этой задачи.

Ранее мы вывели приведенные уравнения для случаев перспективы и слабой перспективы. Вспомним, что в полной перспективной модели матрица камеры определяется как:

$M = \begin{bmatrix} A & b \\ v & 1 \end{bmatrix}$ (1)

где $v$ — некоторый ненулевой вектор размером $1 \times 3$. С другой стороны, для модели слабой перспективы $v = 0$. Мы обнаруживаем, что это свойство делает однородную координату $MX$ равной 1:

$x = MX = \begin{bmatrix} m_1 \\ m_2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ 1 \end{bmatrix} = \begin{bmatrix} m_1X \\ m_2X \\ 1 \end{bmatrix}$ (2)

Следовательно, при переходе от однородных к евклидовым координатам нелинейность проективного преобразования исчезает, и преобразование слабой перспективы действует как простой увеличитель. Мы можем представить проекцию в более компактной форме:

$ M_{affine} = \begin{bmatrix} m_1X \\ m_2X \end{bmatrix} = [A \ b]X = AX + b$ (3)

Таким образом, теперь мы используем аффинную модель камеры для выражения связи между точкой $X_j$ в 3D и соответствующими наблюдениями в каждой аффинной камере (например, $x_{ij}$ в камере $i$).

Возвращаясь к задаче структуры из движения, нам нужно оценить $m$ матриц $M_i$ и $n$ векторов мировых координат $X_j$. Такая система содержит всего $8m + 3n$ неизвестных, на основе $mn$ наблюдений. Каждое наблюдение создает 2 ограничения на камеру, поэтому имеется $2mn$ уравнений с $8m + 3n$ неизвестными.

Мы можем использовать это уравнение, чтобы определить нижнюю границу количества соответствующих наблюдений в каждом из изображений, которые нам необходимы. Например, если у нас есть $m = 2$ камеры, то нам нужно иметь как минимум $n = 16$ точек в 3D. Однако как решить эту задачу, когда у нас достаточно соответствующих точек, помеченных на каждом изображении?

2 Метод факторизации Томаси и Канеде

В этой части мы рассмотрим метод факторизации Томаси и Канеде для решения задачи аффинной структуры из движения. Этот метод состоит из двух основных этапов: центрирования данных и собственно факторизации.

Рисунок 2: Центроид наблюдаемых точек

На рисунке 2 приведен пример центрирования - все точки изображения размещаются таким образом, чтобы их центроид находился в начале координат в плоскости изображения. Аналогично мы размещаем систему мировых координат так, чтобы начало координат находилось в центроиде 3D точек. Основная идея этого этапа — центрирование данных в начале координат. Для этого для каждого изображения $i$ мы переопределяем новые координаты $\hat{x}{ij}$ для каждой точки изображения $x_i$:}$, вычитая их центроид $\bar{x

$\hat{x}{ij} = x} - \bar{xi = x$ (4)} - \frac{1}{n} \sum_{j=1}^{n} x_{ij

Напомним, что задача аффинной структуры из движения позволяет нам определить взаимосвязь между точками изображения $x_{ij}$, переменными матрицы камеры $A_i$ и $b_i$, и 3D точками $X_j$ как:

$x_{ij} = A_i X_j + b_i$ (5)

После этапа центрирования мы можем объединить определение центрированных точек изображения $\hat{x}_{ij}$ из уравнения (4) и аффинное выражение из уравнения (5):

$\hat{x}{ij} = x = $} - \frac{1}{n} \sum_{k=1}^{n} x_{ik
$= A_i X_j - \frac{1}{n} \sum_{k=1}^{n} A_i X_k = A_i(X_j - \frac{1}{n} \sum_{k=1}^{n} X_k) = $
$ = A_i(X_j - \bar{X}) = A_i \hat{X}_j$ (6)

Как видно из уравнения (6), если мы переместим начало системы мировых координат в центроид $\bar{X}$, то центрированные координаты точек изображения $\hat{x}_{ij}$ и центрированные координаты 3D точек $\hat{X}_j$ связаны только одной матрицей $2 \times 3$ $A_i$. В конечном итоге этап центрирования метода факторизации позволяет нам создать компактное матричное произведение для связи 3D структуры с наблюдаемыми точками на множестве изображений.

Однако заметим, что в матричном произведении $\hat{x}{ij} = A_i \hat{X}_j$ у нас есть доступ только к значениям в левой части уравнения. Таким образом, нам нужно каким-то образом выделить матрицы движения $A_i$ и структуру $X_j$. Используя все наблюдения для всех камер, мы можем построить матрицу измерений $D$, состоящую из $n$ наблюдений в $m$ камерах (помните, что каждая запись $\hat{x}$ — это вектор $2 \times 1$):

$D = \begin{bmatrix} \hat{x}{11} & \hat{x}} & \dots & \hat{x{1n} \\ \hat{x}} & \hat{x{22} & \dots & \hat{x}} \\ \vdots & \vdots & \ddots & \vdots \\ \hat{x{m1} & \hat{x}$ (7)} & \dots & \hat{x}_{mn} \end{bmatrix

Теперь вспомним, что из-за нашего аффинного предположения, $D$ может быть выражена как произведение матрицы движения $2m \times 3$ $M$ (которая включает матрицы камер $A_1, \dots, A_m$) и матрицы структуры $3 \times n$ $S$ (которая включает 3D точки $X_1, \dots, X_n$). Важный факт, который мы будем использовать, заключается в том, что $rank(D) = 3$, поскольку $D$ — это произведение двух матриц, максимальное измерение которых равно 3.

Чтобы разложить $D$ на $M$ и $S$, мы будем использовать сингулярное разложение:

$D = U\Sigma V^T = \begin{bmatrix} u_1 & \dots & u_n \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & 0 & 0 & \dots & 0 \\ 0 & \sigma_2 & 0 & 0 & \dots & 0 \\ 0 & 0 & \sigma_3 & 0 & \dots & 0 \\ 0 & 0 & 0 & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \dots & 0 \end{bmatrix} \begin{bmatrix} v_1^T \\ \vdots \\ v_n^T \end{bmatrix} = $

$ = \begin{bmatrix} u_1 & u_2 & u_3 \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \begin{bmatrix} v_1^T \\ v_2^T \\ v_3^T \end{bmatrix} = U_3\Sigma_3V_3^T$ (8)

В этом разложении $\Sigma_3$ определяется как диагональная матрица, образованная ненулевыми сингулярными значениями, в то время как $U_3$ и $V_3^T$ получаются путем взятия соответствующих трех столбцов матрицы $U$ и строк матрицы $V^T$ соответственно.

К сожалению, на практике $rank(D) > 3$ из-за шума измерений и аффинного приближения камеры. Однако мы помним замечательное свойство сингулярного разложения, что когда $rank(D) > 3$, $U_3W_3V_3^T$ все еще остается наилучшим возможным приближением ранга 3 для $MS$ в смысле нормы Фробениуса.

При внимательном рассмотрении мы видим, что матричное произведение $\Sigma_3V_3^T$ образует матрицу размером $3 \times n$, что точно соответствует размеру матрицы структуры $S$. Аналогично, $U_3$ — это матрица размером $2m \times 3$, что соответствует размеру матрицы движения $M$.

Хотя такой способ сопоставления компонентов SVD-разложения с $M$ и $S$ приводит к физически и геометрически правдоподобному решению задачи аффинной структуры из движения, этот выбор не является единственным решением. Например, мы также могли бы установить матрицу движения как $M = U_3\Sigma_3$, а матрицу структуры как $S = V_3^T$, поскольку в обоих случаях матрица наблюдений $D$ остается той же.

Так какое разложение выбрать? В своей работе Томаси и Канеде пришли к выводу, что наиболее надежным выбором факторизации является $M = U_3\sqrt{\Sigma_3}$ и $S = \sqrt{\Sigma_3}V_3^T$.

Тем не менее, мы обнаруживаем внутреннюю неоднозначность в любом выборе факторизации $D = MS$, поскольку в разложение можно вставить любую произвольную обратимую матрицу $3 \times 3$ $A$:

$D = MA A^{-1}S = (MA)(A^{-1}S)$ (9)

Это означает, что матрицы камер, полученные из движения $M$, и 3D точки, полученные из структуры $S$, определяются с точностью до умножения на общую матрицу $A$. Следовательно, наше решение недоопределено и требует дополнительных ограничений для разрешения этой аффинной неоднозначности. Несмотря на то, что параллельность линий сохраняется, метрический масштаб элементов матрицы и координат точек остаются неизвестными.

Другой важный класс неоднозначностей для реконструкции — это неоднозначность подобия, которая возникает, когда реконструкция верна с точностью до преобразования подобия (вращение, перенос и масштабирование). Реконструкция только с неоднозначностью подобия известна как метрическая реконструкция. Эта неоднозначность существует даже при внутренней калибровке камер. Хорошая новость заключается в том, что для откалиброванных камер неоднозначность подобия является единственной возможной неоднозначностью.

Тот факт, что невозможно восстановить абсолютный масштаб сцены по изображениям, довольно интуитивен. Масштаб объекта, абсолютное положение и каноническая ориентация всегда будут неизвестны, если мы не сделаем дополнительные предположения (например, знаем высоту дома на рисунке) или не включим дополнительные данные о матрице переноса. Это происходит потому, что одни атрибуты могут компенсировать другие. Например, чтобы получить то же изображение, мы можем просто отодвинуть объект назад и соответствующим образом масштабировать его.

Один из примеров устранения неоднозначности подобия возник во время процедуры калибровки камеры, когда мы сделали предположение, что знаем расположение калибровочных точек относительно мировой системы координат. Это позволило нам узнать размер квадратов шахматной доски для определения метрического масштаба 3D структуры.

3. Структура из движения с перспективными преобразованиями камер (метод разложения)

После изучения упрощённой задачи аффинной структуры из движения давайте рассмотрим общий случай для проективных камер $M_i$.

В общем случае с проективными камерами каждая матрица камеры $M_i$ содержит 11 степеней свободы, поскольку она определена с точностью до масштабного множителя:

$M_i = \begin{bmatrix} a_{11} & a_{12} & a_{13} & b_1 \\ a_{21} & a_{22} & a_{23} & b_2 \\ a_{31} & a_{32} & a_{33} & 1 \end{bmatrix}$ (10)

Более того, в общем случае решения определение матриц структуры из движения могут быть определены с точностью до проективного преобразования, как и при афинной неоднозначности. Мы всегда можем произвольно применить проективное преобразование $4 \times 4$ $H$ к матрице движения, при условии, что мы также преобразуем матрицу структуры с помощью обратного преобразования $H^{-1}$. Результирующие наблюдения в плоскости изображения останутся прежними.

Аналогично аффинному случаю, мы можем сформулировать общую задачу структуры из движения как оценку как $m$ матриц движения $M_i$, так и $n$ 3D точек $X_j$ на основе $mn$ наблюдений $x_{ij}$. Поскольку камеры и точки могут быть восстановлены только с точностью до проективного преобразования $4 \times 4$ с учётом масштаба (15 параметров), у нас есть $11m + 3n - 15$ неизвестных в $2mn$ уравнениях.

Из этих фактов мы можем определить необходимое количество видов и наблюдений, требуемых для решения неизвестных.

4. Алгебраический подход к SFM с перспективой

Теперь рассмотрим алгебраический подход, который использует концепцию фундаментальной матрицы $F$ для решения задачи оценки структуры из движения для двух камер. В отличии от метода разложения, в алгебраическом подходе мы рассматриваем последовательные пары камер для определения матриц камер $M_1$ и $M_2$ с точностью до перспективного преобразования. Затем мы находим перспективное преобразование $H$ такое, что $M_1H = [I \ 0]$ и $M_2H = [A \ B]$.

Как показано на рисунке 3, основная идея алгебраического подхода заключается в вычислении двух матриц камер $M_1$ и $M_2$, которые могут быть вычислены только с точностью до перспективного преобразования $H$.

Поскольку каждая $M_i$ может быть вычислена только с точностью до перспективного преобразования $H$, мы всегда можем рассмотреть такое $H$, при котором матрица проекции первой камеры $M_1H^{-1}$ будет канонической. Разумеется, то же преобразование должно быть применено и ко второй камере, что приводит к следующей форме:

$M_1H^{-1} = [I \ 0]$
$M_2H^{-1} = [A \ b]$ (11)

Для выполнения этой задачи сначала необходимо вычислить фундаментальную матрицу $F$ с помощью алгоритма восьми точек. Далее матрица $F$ используется для оценки проективных матриц камер $M_1$ и $M_2$.

Для этой оценки определим 3D точку $P$ и соответствующие наблюдения на изображениях $p$ и $p'$. Поскольку мы применили $H^{-1}$ к обеим матрицам проекции камер, мы также должны применить $H$ к структуре, получая $P_e = HP$.
Таким образом, мы можем связать координаты пикселей $p$ и $p'$ с преобразованной структурой следующим образом:

$p = M_1P = M_1H^{-1}HP = [I \ 0]P_e$
$p' = M_2P = M_2H^{-1}HP = [A \ b]P_e$ (12)

Интересное свойство между двумя соответствиями изображений $p$ и $p'$ возникает при подстановках:

$p' = [A \ b] P_e =$
$= A[I \ 0] P_e + b =$
$= Ap + b$ (13)

Используя уравнение (13), мы можем записать векторное произведение между $p'$ и $b$ как:

$p' \times b = (Ap + b) \times b = Ap \times b$ (14)

По определению векторного произведения, $p' \times b$ перпендикулярен $p'$. Поэтому мы можем записать:

$0 = p'^T(p' \times b) = p'^T(Ap \times b) = p'^T \cdot (b \times Ap) = p'^T[b\times] Ap$ (15)

Рассматрев это ограничение более внимательно, можно увидеть, что оно напоминает общее определение фундаментальной матрицы
$p'^TFp = 0$

Если мы установим $F = [b\times] A$, то извлечение $A$ и $b$ снова сводится к задаче разложения.

Давайте начнем с определения $b$. Снова используя определение векторного произведения, мы можем записать:

$F^\top b = [[b\times] A]^\top b = 0$ (16)

Поскольку матрица $F$ является сингулярной, вектор $b$ можно вычислить как решение методом наименьших квадратов уравнения $F^\top b = 0$ при условии $|b| = 1$ с помощью сингулярного разложения (SVD).

Как только вектор $b$ становится известным, мы можем вычислить матрицу $A$. Если мы положим $A = −[b\times] F$, то можем проверить, что это определение удовлетворяет условию $F = [b\times] A$:

$[b\times] A' = −[b\times][b\times] F$ $= (bb^\top − |b|^2I)F$ $= bb^\top F + |b|^2F$ $= 0 + 1 · F$ $= F$ (17)

Следовательно, мы определяем два выражения для матриц наших камер $M_1H^{−1}$ и $M_2H^{−1}$:

$\tilde{M}_1 = [I \ 0]$ $\tilde{M}_2 = [−[b\times] F \ b]$ (18)

Прежде чем завершить этот раздел, мы хотим дать геометрическую интерпретацию для вектора $b$. Мы знаем, что $b$ удовлетворяет условию $Fb = 0$. Вспомним эпиполярные ограничения, которые мы вывели в предыдущих конспектах, где было показано, что эпиполы на изображении — это точки, которые отображаются в ноль при преобразовании фундаментальной матрицей (то есть $Fe_2 = 0$ и $F^\top e_1 = 0$). Таким образом, мы видим, что $b$ является эпиполом. Это даёт нам новый набор уравнений для матриц проекции камер (формулы 4.10):

$\tilde{M}_1 = [I \ 0]$ $\tilde{M}_2 = [−[e\times] F \ e]$ (19)

В предыдущих заметках мы рассмотрели, как с помощью ключевых точек можно значительно улучшить наше понимание -сцены. Мы сосредоточились на настройке эполярной геометрии, чтобы связать точки одной плоскости изображения с точками другой без извлечения какой-либо информации о трёхмерной сцене. В этой заметке мы обсудим, как восстановить информацию о трёхмерной сцене из нескольких двумерных изображений.

Рисунок 1: Триангуляция точки Р по двум изображениям

Одной из фундаментальных задач в геометрии множественных видов является задача триангуляции — процесс определения местоположения трёхмерной точки по её проекциям на два или более изображений. В задаче триангуляции с двумя видами у нас есть две камеры с известными внутренними параметрами камеры $K$ и $K'$ соответственно. Нам также известны относительные ориентации и смещения $R$, $T$ этих камер относительно друг друга.

Предположим, что у нас есть точка $P$ в трёхмерном пространстве, которая может быть найдена на изображениях двух камер в точках $p$ и $p'$ соответственно. Хотя местоположение $P$ в данный момент неизвестно, мы можем измерить точные местоположения $p$ и $p'$ на изображении. Поскольку $K$, $K'$, $R$, $T$ известны, мы можем вычислить две линии визирования $ℓ$ и $ℓ'$, которые определяются центрами камер $O_1$, $O_2$ и местоположениями изображений $p$, $p'$. Следовательно, $P$ может быть вычислена как точка пересечения $ℓ$ и $ℓ'$.

Рисунок 2: Ошибки в проекции точки

Хотя этот процесс кажется простым и математически обоснованным, на практике он работает не очень хорошо. В реальном мире из-за того, что наблюдения $p$ и $p'$ зашумлены, а параметры калибровки камеры не являются точными, поиск точки пересечения прямых $ℓ$ и $ℓ'$ может быть проблематичным. В большинстве случаев она вообще не существует, поскольку эти две прямые могут не пересекаться.

1. Линейный метод триангуляции

В этом разделе мы описываем простой линейный метод триангуляции, который решает проблему отсутствия точки пересечения между лучами. Нам даны две точки на изображениях, которые соответствуют друг другу:
$p = MP = (x, y, 1)$
$p' = M'P = (x', y', 1)$

Вспомним, что векторное произведение двух векторов в трехмерном пространстве дает вектор, перпендикулярный обоим исходным векторам.

В нашем случае: * $p = (x, y, 1)$ — это точка на плоскости изображения * $MP$ — это результат умножения матрицы камеры $M$ на координаты 3D точки $P$

Векторы $p$ и $MP$ коллинеарны (лежат на одной прямой или параллельны), а значит $p \times (MP) = 0$

Развернем это векторное произведение в координатной форме:

$p \times (MP) = \begin{vmatrix} i & j & k \\ x & y & 1 \\ M_1P & M_2P & M_3P \end{vmatrix} = 0$

Раскрывая определитель, получаем:

$p \times (MP) = i(yM_3P - M_2P) - j(xM_3P - M_1P) + k(xM_2P - yM_1P) = 0$

Это векторное равенство равно нулю тогда и только тогда, когда каждая его компонента равна нулю:

$x(M_3P) − (M_1P) = 0$
$y(M_3P) − (M_2P) = 0$
$x(M_2P) − y(M_1P) = 0$ (1)

где $M_i$ — это $i$-я строка матрицы $M$.

Подобные ограничения можно сформулировать для $p'$ и $M'$. Используя ограничения обоих изображений, мы можем сформулировать линейное уравнение вида
$AP = 0$, где

$A = \begin{bmatrix} xM_3 − M_1 \\ yM_3 − M_2 \\ x'M'_3 − M'_1 \\ y'M'_3 − M'_2 \end{bmatrix}$ (2)

Это уравнение можно решить с помощью сингулярного разложения (SVD), чтобы найти наилучшую линейную оценку точки $P$.

Другой интересный аспект этого метода заключается в том, что он фактически может обрабатывать триангуляцию из нескольких видов. Для этого нужно просто добавить дополнительные строки к матрице $A$, соответствующие новым ограничениям от дополнительных видов.

Однако этот метод не подходит для проективной реконструкции.
Основная причина - особенность разложения методом SVD, которое решается при ограничении $∥P∥ = 1$. Ограничение $|P| = 1$ означает, что вектор $P$ нормирован, то есть его длина равна единице. Однако при проективных преобразованиях это свойство не сохраняется, так как такие преобразования изменяют длины векторов. Другими словами, сингулярное разложение не является инвариантным относительно проективного преобразования $H$. Например, предположим, что мы заменяем матрицы камер $M$ и $M'$ на матрицы, подвергнутые проективному преобразованию $MH^{-1}$ и $M'H^{-1}$. Тогда матрица линейных уравнений $A$ становится равной $AH^{-1}$. Следовательно, решение $P$ для предыдущей оценки $AP = 0$ будет соответствовать решению $HP$ для преобразованной задачи $(AH^{-1})(HP) = 0$.

Поэтому линейный метод триангуляции вычислительно простой, но часто не является оптимальным решением задачи триангуляции.

2. Нелинейный метод триангуляции

Вместо этого задача триангуляции для реальных сценариев часто математически характеризуется как решение задачи минимизации:

$\min_{\hat{P}} |M\hat{P} - p|^2 + |M'\hat{P} - p'|^2$ (3)

В приведенном уравнении мы стремимся найти точку $\hat{P}$ в 3D пространстве, которая наилучшим образом аппроксимирует $P$, путем нахождения наилучшей оценки методом наименьших квадратов для ошибки репроекции $\hat{P}$ на обоих изображениях.

Ошибка репроекции для 3D точки на изображении — это расстояние между проекцией этой точки на изображении и соответствующей наблюдаемой точкой в плоскости изображения. В случае нашего примера на рисунке 2, поскольку $M$ — это проективное преобразование из 3D пространства в изображение 1, проецируемая точка $\hat{P}$ на изображении 1 равна $M\hat{P}$. Соответствующее наблюдение точки $\hat{P}$ на изображении 1 — это $p$. Таким образом, ошибка репроекции для точки $P$ на изображении 1 равна расстоянию $|M\hat{P} - p|$.

Общая ошибка репроекции, найденная в уравнении (3), представляет собой сумму ошибок репроекции для всех точек на изображении. В случае более чем двух изображений мы просто добавим дополнительные члены расстояния в целевую функцию:

$\min_{\hat{P}} \sum_i |M\hat{P}_i - p_i|^2$ (4)

На практике существует множество очень сложных методов оптимизации, которые дают хорошие приближения к решению задачи. Однако в рамках курса мы сосредоточимся только на одном из этих методов — алгоритме Гаусса-Ньютона для нелинейных наименьших квадратов.

Общая задача нелинейных наименьших квадратов заключается в нахождении $x \in \mathbb{R}^n$, который минимизирует:

$|r(x)|^2 = \sum_{i=1}^m r_i(x)^2$ (5)

где $r$ — любая остаточная функция $r: \mathbb{R}^n \rightarrow \mathbb{R}^m$ такая, что $r(x) = f(x) - y$ для некоторой функции $f$, входных данных $x$ и наблюдения $y$. Задача нелинейных наименьших квадратов сводится к обычной линейной задаче наименьших квадратов, когда функция $f$ линейна. Однако помните, что в общем случае наши матрицы камер не являются аффинными.

Если мы обозначим $e_i$ как вектор $2 \times 1$, $e_i = M\hat{P}_i - p_i$, то мы можем переформулировать нашу задачу оптимизации следующим образом:

$\min_{\hat{P}} \sum_i e_i(\hat{P})^2$ (6)

что может быть идеально представлено как задача нелинейных наименьших квадратов.

В этих заметках мы рассмотрим, как можно использовать популярный алгоритм Гаусса-Ньютона для нахождения приближенного решения этой задачи нелинейных наименьших квадратов. Сначала предположим, что у нас есть достаточно разумная оценка 3D точки $\hat{P}$, которую мы можем вычислить с помощью предыдущего линейного метода.

Ключевая идея алгоритма Гаусса-Ньютона заключается в обновлении нашей оценки путем корректировки её в направлении еще лучшей оценки, которая минимизирует ошибку репроекции. На каждом шаге мы хотим обновить нашу оценку $\hat{P}$ на некоторую величину $\delta P$: $\hat{P} = \hat{P} + \delta P$.

Как выбрать параметр обновления δP? Ключевая идея алгоритма Гаусса-Ньютона заключается в линеаризации остаточной функции вблизи текущей оценки $\hat{P}$. В нашем случае это означает, что остаточная ошибка $e$ точки $P$ может быть представлена как:

$e(\hat{P} + \delta P) \approx e(\hat{P}) + \frac{\partial e}{\partial P} \delta P$ (7)

После этого задача минимизации преобразуется в:

$\min_{\delta P} \left| \frac{\partial e}{\partial P} \delta P - (-e(\hat{P})) \right|^2$ (8)

Когда мы формулируем остаточную функцию таким образом, становится видно, что она принимает формат стандартной задачи линейных наименьших квадратов. Для задачи триангуляции с $N$ изображениями решение линейных наименьших квадратов имеет вид:

$\delta P = -(J^TJ)^{-1}J^Te$ (9)

где:

$e = \begin{bmatrix} e_1 \\ \vdots \\ e_N \end{bmatrix} = \begin{bmatrix} p_1 - M_1\hat{P} \\ \vdots \\ p_n - M_n\hat{P} \end{bmatrix}$ (10)

и

$J = \begin{bmatrix} \frac{\partial e_1}{\partial \hat{P}_1} & \frac{\partial e_1}{\partial \hat{P}_2} & \frac{\partial e_1}{\partial \hat{P}_3} \\ \vdots & \vdots & \vdots \\ \frac{\partial e_N}{\partial \hat{P}_1} & \frac{\partial e_N}{\partial \hat{P}_2} & \frac{\partial e_N}{\partial \hat{P}_3} \end{bmatrix}$ (11)

Важно отметить, что вектор остаточной ошибки для конкретного изображения $e_i$ является вектором размера $2 \times 1$, поскольку в плоскости изображения есть два измерения. Следовательно, в простейшем случае с двумя камерами ($N = 2$) вектор остаточной ошибки $e$ будет иметь размер $2N \times 1 = 4 \times 1$, а матрица Якоби $J$ — размер $2N \times 3 = 4 \times 3$.

Этот метод легко обрабатывает множественные виды, так как дополнительные изображения учитываются путем добавления соответствующих строк к вектору $e$ и матрице $J$. После вычисления обновления $\delta P$ мы можем просто повторить процесс фиксированное количество шагов или до численной сходимости.

Важное свойство алгоритма Гаусса-Ньютона заключается в том, что наше предположение о линейности остаточной функции вблизи оценки не гарантирует сходимость. Поэтому на практике всегда полезно установить верхнюю границу количества обновлений оценки.

Резюме

Триангуляция представляет собой фундаментальный процесс определения местоположения трёхмерной точки по её проекциям на два или более изображений. В основе этого метода лежит работа с двумя камерами, для которых известны внутренние параметры $K$ и $K'$, а также их относительные ориентации и смещения $R$ и $T$.

При наличии трёхмерной точки $P$, которая проецируется на изображения в точках $p$ и $p'$, задача сводится к вычислению линий визирования $\ell$ и $\ell'$, определяемых центрами камер $O_1$ и $O_2$. В идеальном случае точка $P$ находится в точке пересечения этих линий. Однако на практике из-за шума в измерениях и неточностей калибровки камер точное пересечение линий может отсутствовать.

Существует два основных подхода к решению задачи триангуляции.

Линейный метод основан на использовании векторного произведения для формирования системы линейных уравнений вида $AP = 0$, которая решается с помощью сингулярного разложения (SVD). Несмотря на вычислительную простоту, этот метод имеет существенные ограничения, главным из которых является невозможность корректной работы с проективными преобразованиями.

Более эффективным является нелинейный метод триангуляции, который формулирует задачу как минимизацию ошибки репроекции. Основная идея заключается в поиске такой трёхмерной точки $\hat{P}$, которая обеспечивает минимальное расстояние между её проекциями на изображения и наблюдаемыми точками.

Для решения этой оптимизационной задачи широко применяется алгоритм Гаусса-Ньютона. Метод работает путём итеративного обновления оценки точки через вычисление остаточной ошибки $e$ и матрицы Якоби $J$. На каждом шаге происходит корректировка оценки по формуле:

$\delta P = -(J^TJ)^{-1}J^Te$

Важным преимуществом нелинейного подхода является его способность работать с множественными видами — дополнительные изображения просто добавляются в систему уравнений. При этом алгоритм обеспечивает более точную оценку положения точки за счёт минимизации суммарной ошибки репроекции на всех изображениях.

Несмотря на эффективность, метод требует разумной начальной оценки и контроля количества итераций для обеспечения сходимости. Тем не менее, нелинейная триангуляция остаётся предпочтительным выбором для практических приложений, где требуется высокая точность реконструкции трёхмерных сцен.

Введение

В предыдущих разделах мы изучали методы расчёта внутренних и внешних параметров камеры. Это можно сделать с помощью стандартной процедуры калибровки камеры или используя знания о перпендикулярных плоскостях по одному изображению. В результате этих вычислений мы смогли получить определённые характеристики трёхмерного пространства.

Однако в общем случае невозможно восстановить полную структуру трёхмерного мира, опираясь только на одно изображение. Причина этого кроется во внутренней неоднозначности процесса отображения трёхмерного пространства на двумерную плоскость — часть информации неизбежно теряется при таком преобразовании.

Рисунок 1: Проблема неоднозначности

Рассмотрим характерный пример, показанный на рисунке 1. На первый взгляд может показаться, что человек действительно удерживает Пизанскую башню. Только при внимательном изучении изображения становится понятно, что это всего лишь оптическая иллюзия, возникшая из-за проецирования объектов с разной глубиной на плоскость изображения.

Если же рассмотреть эту сцену с совершенно другой точки зрения, иллюзия исчезает, и мы можем определить правильное расположение объектов в пространстве. Именно поэтому использование нескольких точек обзора является ключевым для точного понимания структуры сцены.

1. Эпиполярная геометрия

Эпиполярная геометрия представляет собой раздел компьютерной геометрии, который изучает взаимосвязь между точками на разных изображениях, ограничения на их расположение при проецировании и геометрические соотношения между камерами.

Рисунок 2: Основные элементы эпиполярной геометрии

Рассмотрим основные элементы эпиполярной геометрии, изображённые на рисунке 2:

• Две камеры наблюдают одну и ту же трёхмерную точку $P$
• Проекции точки $P$ на плоскости изображений находятся в точках $p$ и $p'$
• Центры камер расположены в точках $O_1$ и $O_2$
• Линия, соединяющая центры камер, называется базисом (оранжевая линия)
• Плоскость, образованная двумя центрами камер и точкой $P$, называется эпиполярной плоскостью (изображена серым цветом)
• Эпиполы — точки пересечения базиса с плоскостями изображений ($e$ и $e'$)
• Эпиполярные линии — прямые, образованные пересечением эпиполярной плоскости с плоскостями изображений (голубые отрезки)

Рисунок 3: Пример расположения эпиполярных линий и ключевых точек

На рисунке 3 показан пример эпиполярных линий и соответствующих ключевых точек, нанесённых на пару изображений. Эта визуализация демонстрирует, как эпиполярная геометрия помогает установить связь между точками на разных снимках.

Таким образом, эпиполярная геометрия помогает установить связи между изображениями одной и той же сцены, снятыми с разных точек зрения, и восстанавливать трёхмерную структуру.

Рисунок 4: Частный случай эпиполярной геометрии

Рассмотрим интересную ситуацию, когда плоскости изображений расположены параллельны друг другу (см. рисунок 4). В этом случае эпиполы $e$ и $e'$ располагаются в бесконечности. Это происходит потому, что базис, соединяющий центры камер $O_1$ и $O_2$, параллелен плоскостям изображений. Эпиполярные линии становятся параллельными оси $u$ на плоскости изображения.

Этот частный случай имеет важное практическое значение, особенно при работе с выравниванием изображений, о чём будет подробно рассказано в следующем разделе.

В практических ситуациях точное расположение трёхмерной точки $P$ неизвестно. Но мы можем определить её проекции $p, p'$ на плоскости изображений, местоположение, ориентацию и внутренние параметры камер.

Кроме того, зная положения камер $O_1$, $O_2$ и положение проекции точки $p$ на одном изображении, можно определить эпиполярную плоскость и найти эпиполярные линии на основе этой плоскости. Это существенно упрощает поиск соответствующей ключевой точки на других изображениях. Это свойство делает эпиполярную геометрию мощным инструментом в задачах компьютерного зрения и трёхмерной реконструкции сцены.

2. Эссенциальная матрица

Для создания эффективного способа отображения точек и эпиполярных линий между разными видами сцены мы используем базовую структуру эпиполярной геометрии. В этой системе матрицы проекции $M$ и $M'$ отвечают за преобразование трёхмерных точек в двумерные координаты на плоскостях изображений. Мировая система координат связывается с первой камерой, при этом вторая камера смещается относительно первой через последовательное применение поворота $R$ и переноса $T$.

Рисунок 5: Расположение второй камеры относительно первой

В результате того, что за точку отсчета мировых координат мы принимаем центр камеры $O_1$, матрицы проекции принимают следующий вид:

$M = K \begin{bmatrix} I & 0 \end{bmatrix}$ (2)

$M' = K' \begin{bmatrix} R & -RT \end{bmatrix}$

где $K$ и $K'$ представляют внутренние параметры камер, $I$ — единичная матрица, $R$ отвечает за поворот, а $T$ — за перенос (вектор $O_1 O_2$).

Рассмотрим частный случай с каноническими камерами:

$K = K' = I$

$p'$ - это координаты проекции точки в системе координат второй камеры. Координаты точки $p'$ в системе координат первой камеры определяются как $Rp' + T$.

Поскольку векторы $Rp' + T$ и $T$ лежат в эпиполярной плоскости, их векторное произведение даёт вектор, перпендикулярный этой плоскости.
Благодаря свойствам дистрибутивности векторного произведения получаем результат:

$T \times (Rp' + T) = T \times (Rp')$

Точка $p$, лежащая в эпиполярной плоскости, ортогональна вектору $T \times (Rp')$, что даёт ограничение:

$p^T \cdot [T \times (Rp')] = 0$ (3)

Напомним, векторное произведение — это операция над двумя векторами в трёхмерном пространстве, результатом которой является новый вектор. Результат — вектор, перпендикулярный обоим исходным векторам, его длина равна площади параллелограмма, построенного на исходных векторах, а направление определяется правилом правой руки

Пусть даны два вектора:

$\vec{a} = (a_1, a_2, a_3)$

$\vec{b} = (b_1, b_2, b_3)$

Их векторное произведение:

$\vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$

где $\vec{i}, \vec{j}, \vec{k}$ — единичные векторы по осям координат.

Формула для вычисления имеет вид:

$\vec{a} \times \vec{b} = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1)$

Вернемся к эпиполярной геометрии.

Используя аппарат линейной алгебры, векторное произведение можно представить в виде матрично-векторного умножения:

$a \times b = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = [a\times]b$ (4)

Преобразуя выражение с учётом этого представления, получаем:

$p^T[T\times]Rp' = 0$ (5)

Матрица $E = [T\times]R$ называется эссенциальной матрицей и даёт компактную форму эпиполярного ограничения:

$p^TEp' = 0$ (6)

Эссенциальная матрица — это матрица размером $3 \times 3$, содержащая 5 степеней свободы. Она имеет ранг 2 и является сингулярной.

Эта матрица полезна для вычисления эпиполярных линий. Например, $l' = E^Tp$ даёт эпиполярную линию в плоскости изображения второй камеры, а $l = Ep'$ — в плоскости первой камеры.

Важные свойства эссенциальной матрицы: * Её скалярное произведение с эпиполями равно нулю: $E^Te = Ee' = 0$ * Для любой точки $x$ (кроме $e$) в изображении первой камеры соответствующая эпиполярная линия во второй камере содержит эпиполь $e'$

Таким образом, эссенциальная матрица является фундаментальным инструментом для работы с эпиполярной геометрией и установления связей между точками на разных изображениях.

3. Фундаментальная матрица

Фундаментальная матрица — это важный инструмент в эпиполярной геометрии, который обобщает концепцию эссенциальной матрицы на случай камер с нетривиальными внутренними параметрами.

Рассмотрим матрицы проекции для двух камер:

$M = K \begin{bmatrix} I & 0 \end{bmatrix}$

$M' = K' \begin{bmatrix} R & -RT \end{bmatrix}$ (7)

Для работы с неканоническими камерами введём обозначения: * $p_c = K^{-1}p$ — проекция точки $p$ для канонической камеры * $p'_c = K'^{-1}p'$ — проекция точки $p'$ для канонической камеры

В каноническом случае (единичная матрица $K$) выполняется соотношение:

$p_c^T [T \times] R p'_c = 0$ (8)

Однако, с учетом преобразований внутренних параметров камеры, получаем:

$p^T K^{-T} [T \times] R K'^{-1} p' = 0$ (9)

Матрица $F = K'^{-T} [T \times] R K^{-1}$ называется фундаментальной матрицей.
Она обобщает свойства эссенциальной матрицы, учитывает параметры камер $K$ и $K'$ и содержит информацию о взаимном положении камер. (вращение $R$ и перенос $T$). очками на разных изображениях Фундаментальная матрица имеет 7 степеней свободы (против 5 у эссенциальной матрицы), позволяет находить эпиполярные линии без знания 3D-координат точек и работает даже при неизвестных параметрах камер.

Таким образом, фундаментальная матрица даёт мощный инструмент для установления связей между точками на разных изображениях, не требуя полной информации о параметрах камер или трёхмерных координатах точек.

4. Алгоритм восьми точек для вычисления фундаментальной матрицы

Алгоритм восьми точек — это метод оценки фундаментальной матрицы по двум изображениям сцены без знания параметров камер. Метод был предложен Лонге-Хиггинсом в 1981 году и расширен Хартли в 1995 году.

Рисунок 6: Ключевые точки и их соответствие на двух изображениях

Для работы алгоритма требуется минимум 8 пар соответствующих точек между двумя изображениями. Каждая пара точек $p_i = (u_i, v_i, 1)$ и $p'_i = (u'_i, v'_i, 1)$ даёт ограничение $p_i^TFp'_i = 0$.

Математически ограничение можно представить в виде:

$\begin{bmatrix} u_iu'i & v'_iu_i & u_iu'_i & v_iu'_i & v_iv'_i & v_iu'_i & v'_i & 1 \end{bmatrix} \begin{bmatrix} F \end{bmatrix} = 0$} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33

Практическая реализация для $N ≥ 8$ соответствий формируется система уравнений:

$Wf = 0$,

где: * $W$ — матрица размером $N × 9$ * $f$ — вектор элементов фундаментальной матрицы

На практике эффективнее использовать больше восьми соответствий и создавать более крупную матрицу W, поскольку это снижает влияние зашумлённых измерений.

Решение этой системы однородных уравнений можно найти методом наименьших квадратов с помощью сингулярного разложения (SVD), так как матрица W является дефектной по рангу.

SVD даёт оценку фундаментальной матрицы $\hat{F}$, которая может иметь полный ранг. Однако истинная фундаментальная матрица имеет ранг 2, поэтому нужно искать решение, которое является наилучшим приближением ранга 2 для $\hat{F}$.

Математически это формулируется как задача оптимизации:

$\min_F ||F - \hat{F}||_F$ при условии $\det(F) = 0$

где: * $||\cdot||_F$ — норма Фробениуса * $\det(F) = 0$ — условие, обеспечивающее ранг матрицы равный 2

Напомним, сингулярное разложение (SVD) для приблизительной оценки матрицы имеет вид:

$\hat{F} = U\Sigma V^T$

Искомая матрица $F$ будет иметь наилучшее приближение 2 ранга:

$F = U \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & 0 \end{bmatrix} V^T$

где $\sigma_1$ и $\sigma_2$ — первые два сингулярных числа матрицы $\hat{F}$.

Такой подход гарантирует схранение геометрических свойств фундаментальной матрицы, минимизацию отклонения от исходной оценки и сохранение ранга 2.

Таким образом, алгоритм позволяет оценить фундаментальную матрицу без знания параметров камер и является основой для многих задач стереовидения и трёхмерной реконструкции.

5. Нормализованный алгоритм восьми точек

Стандартная реализация алгоритма восьми точек часто даёт неточные результаты. Обычное расстояние между точкой $p_i$ и соответствующей эпиполярной линией $l_i = Fp'_i$ может достигать 10 и более пикселей.

Основная проблема заключается в том, что матрица $W$ плохо обусловлена, это создает проблемы для алгоритма SVD. Основная причина - большие абсолютные значения координат точек (например, $p_i = (1832, 1023, 1)$) Проблема усугубляется, если точки $p_i$ и $p'_i$ находятся в небольшой области изображения, при наличии одного большого сингулярного значения при малых остальных.

Для решения этой проблемы и улучшения точности используется нормализация координат. 1. Сдвиг координат так, чтобы начало новой системы находилось в центре масс точек 2. Масштабирование координат так, чтобы среднеквадратичное расстояние от начала координат равнялось 2 пикселям

Для реализации используются матрицы преобразования $T$ и $T'$, которые выполняют сдвиг на центроид и применяют масштабирующий коэффициент $\left(\frac{2N}{\sum_{i=1}^N||x_i - \bar{x}||^2}\right)^{1/2}$

Нормализованные координаты вычисляются как:
$q_i = Tp_i$
$q'_i = T'p'_i$

Далее, используя нормализованные координаты, вычисляется матрица $F_q$ стандартным методом и производится денормализация:

$F = T'^TF_qT$

Нормализованный алгоритм обеспечивает:
- Более точные результаты в реальных приложениях
- Улучшенную обусловленность матрицы $W$
- Снижение влияния больших значений координат
- Повышение точности оценки фундаментальной матрицы

Такой подход значительно улучшает качество оценки фундаментальной матрицы и является предпочтительным методом для практического применения.

6. Выравнивание изображений (Image Rectification)

Особое свойство эпиполярной геометрии проявляется, когда два изображения параллельны друг другу. Рассмотрим частный случай параллельных плоскостей изображений.

Камеры имеют одинаковую матрицу $K$, отсутствует относительное вращение ($R = I$) и есть только перенос вдоль оси $x$ ($T = (T_x, 0, 0)$)

В этом случае эссенциальная матрица принимает вид:

$E = [T×]R = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \end{bmatrix}$ (17)

Направление эпиполярной линии для точки $p' = (u', v', 1)$ вычисляется как:

$l = Ep' = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -T_x \\ 0 & T_x & 0 \end{bmatrix} \begin{bmatrix} u' \\ v' \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ -T_x \\ T_xv' \end{bmatrix}$ (18)

В этом случае направление эпиполярной линии $l$ горизонтально. Аналогично, направление $l'$ также горизонтально, а все эпиполярные линии параллельны друг другу.
Такое выравнивание изображений позволяет значительно упростить поиск соответствий между точками и упрощает стереообработку и трёхмерную реконструкцию сцены.

Рисунок 7: Ректификация (выравнивание) изображений

Если мы используем эпиполярное ограничение $p^T E p' = 0$, то приходим к тому, что $v = v'$. Это показывает, что точки $p$ и $p'$ имеют одинаковую координату $v$.

Следовательно, между соответствующими точками существует очень простая взаимосвязь. Поэтому выравнивание (процесс приведения любых двух заданных изображений к параллельному виду) становится полезным при определении взаимосвязей между соответствующими точками на изображениях.

Рисунок 8: Вычисление гомографий ректификации

Выравнивание пары изображений не требует знания матриц камер $K$ и $K'$ или относительного преобразования $R$, $T$ между ними. Вместо этого можно использовать фундаментальную матрицу, оценённую с помощью нормализованного алгоритма восьми точек.

После получения фундаментальной матрицы можно вычислить эпиполярные линии $l_i$ и $l'_i$ для каждой пары соответствующих точек $p_i$ и $p'_i$.

На основе набора эпиполярных линий можно оценить эпиполи $e$ и $e'$ для каждого изображения. Это возможно потому, что эпиполь лежит в точке пересечения всех эпиполярных линий.

В реальных условиях из-за зашумлённых измерений все эпиполярные линии не пересекаются в одной точке. Поэтому вычисление эпиполя можно найти путём минимизации среднеквадратичной ошибки подгонки точки ко всем эпиполярным линиям.

Каждая эпиполярная линия может быть представлена в виде вектора $l$ так, что все точки на линии (в однородных координатах) принадлежат множеству ${x | l^T x = 0}$. Если определить каждую эпиполярную линию как $l_i = [l_{i,1}, l_{i,2}, l_{i,3}]^T$, то можно сформулировать линейную систему уравнений и решить её с помощью сингулярного разложения (SVD) для нахождения эпиполя $e$.

$\begin{bmatrix} l^T_1 \\ \vdots \\ l^T_n \end{bmatrix} e = 0$

После нахождения эпиполей $e$ и $e'$, мы, скорее всего, обнаружим, что они не являются точками на бесконечности вдоль горизонтальной оси. Если бы это было так, то изображения уже были бы параллельными по определению.

Это наводит на мысль: можно ли найти гомографию, которая отобразит эпиполь $e$ в бесконечность вдоль горизонтальной оси?

Все что нам нужно - это найти пару гомографий $H_1$ и $H_2$, применить их к изображениям и отобразить эпиполи в бесконечность.

Начнём с поиска гомографии $H_2$, которая отображает второй эпиполь $e'$ в точку на горизонтальной оси в бесконечности $(f, 0, 0)$.

Хотя существует множество вариантов такой гомографии, на практике хорошо работает условие, при котором гомография действует как преобразование и применяет перенос и поворот к точкам около центра изображения.

Первый шаг — сдвиг второго изображения так, чтобы его центр оказался в точке $(0, 0, 1)$ в однородных координатах. Это достигается применением матрицы переноса.

$T = \begin{bmatrix} 1 & 0 & -\frac{width}{2} \\ 0 & 1 & -\frac{height}{2} \\ 0 & 0 & 1 \end{bmatrix}$ (20)

После применения переноса мы выполняем поворот, чтобы разместить эпиполь на горизонтальной оси в некоторой точке $(f, 0, 1)$.

Если перенесённый эпиполь $T e'$ находится в однородных координатах $(e'_1, e'_2, 1)$, то применяемый поворот определяется следующим образом:

$R = \begin{bmatrix} \alpha\frac{e'_1}{\sqrt{e'^2_1 + e'^2_2}} & \alpha\frac{e'_2}{\sqrt{e'^2_1 + e'^2_2}} & 0 \\ -\alpha\frac{e'_2}{\sqrt{e'^2_1 + e'^2_2}} & \alpha\frac{e'_1}{\sqrt{e'^2_1 + e'^2_2}} & 0 \\ 0 & 0 & 1 \end{bmatrix}$ (21)

где параметр $\alpha$ определяется следующим образом:
$\alpha = 1$, если $e'_1 \geq 0$
$\alpha = -1$ в противном случае.

После применения этого поворота заметим, что для любой точки $(f, 0, 1)$ перевод её в точку на бесконечности по горизонтальной оси $(f, 0, 0)$ требует применения преобразования:

$G = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -\frac{1}{f} & 0 & 1 \end{bmatrix}$

После применения этого преобразования мы наконец получаем эпиполь в бесконечности, поэтому можем вернуться к обычному пространству изображения.

Таким образом, гомография $H_2$, которую мы применяем ко второму изображению для его выравнивания, имеет вид:

$H_2 = T^{-1}GRT$ (23)

Теперь, когда мы нашли допустимую $H_2$, нам нужно найти подходящую гомографию $H_1$ для первого изображения. Мы делаем это путём поиска такого преобразования $H_1$, которое минимизирует сумму квадратов расстояний между соответствующими точками изображений:

$\arg\min_{H_1} \sum_{i} ||H_1p_i - H_2p'_i||^2$

В результате мы получаем пару гомографий ($H_1$, $H_2$), которые позволяют выровнять изображения, сделать эпиполярные линии горизонтальными и упростить поиск соответствий между точками.

Можно доказать, что подходящая гомография $H_1$ имеет следующий вид:

$H_1 = H_A H_2 M$ (25)

где: * $F = [e]\times M$ * $H_A$ — специальная матрица вида:

$H_A = \begin{bmatrix} a_1 & a_2 & a_3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ (26)

Здесь $(a_1, a_2, a_3)$ — компоненты определённого вектора $a$, который будет вычислен позже.

Разберём структуру этого выражения:

Матрица $H_A$ представляет собой линейное преобразование вдоль оси $x$, координаты $y$ и $z$ остаются неизменными. $H_2$ — уже известная гомография для второго изображения
$M$ — вспомогательная матрица, связанная с фундаментальной матрицей $F$
$[e]\times$ — кососимметричная матрица, построенная на векторе $e$

Кососимметричная матрица обладает свойством $A = A^3$ с точностью до масштаба.

Поскольку: * Матрица векторного произведения $[e]\times$ — кососимметричная * Фундаментальная матрица $F$ известна только с точностью до масштаба

Получаем:

$F = [e]\times M = [e]\times[e]\times[e]\times M = [e]\times[e]\times F$ (27)

Отсюда следует:

$M = [e]\times F$ (28)

Важно заметить: если к столбцам $M$ добавить любое скалярное кратное вектора $e$, равенство $F = [e]\times M$ сохраняется.

Поэтому более общий вид $M$:

$M = [e]\times F + ev^T$ (29)

На практике хорошо работает выбор $v^T = [1, 1, 1]$.

Для нахождения $H_1$ нужно вычислить значения вектора $a$ в матрице $H_A$.

Задача сводится к минимизации:

$\arg\min_{H_A} \sum_{i} ||H_A\hat{p}_i - \hat{p}'_i||^2$ (30)

где: * $\hat{p}_i = H_2Mp_i$ * $\hat{p}'_i = H_2p'_i$

При этом $H_2$ и $M$ уже известны.

Введение

На предыдущих лекциях мы обсуждали, как можно преобразовывать точки из реального трёхмерного мира в цифровые изображения, используя внешние и внутренние характеристики камер. Мы рассмотрели, как можно использовать известную структуру калибровочной установки и соответствующие изображения для определения характеристик камеры.

Теперь мы обратимся к смежной проблеме: можно ли восстановить известную структуру трёхмерного мира, если у нас есть единственное изображение и известны свойства камеры, которой это изображение было сделано? И наконец мы рассмотрим алгоритм калибровки камеры и измерения углов между плоскостями на одиночном изображении.

1. Преобразования в 2D пространстве

Чтобы лучше понять, как мы можем извлекать информацию из изображений, сначала необходимо разобраться с различными преобразованиями в двумерном пространстве.

Изометрические преобразования — это преобразования, сохраняющие расстояния. В своей базовой форме изометрия может быть описана как вращение $R$ и перенос $t$. Математически они определяются следующим образом:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

где $(x', y', 1)^T$ — точка, полученная после изометрического преобразования.

Преобразования подобия — это преобразования, сохраняющие форму. Интуитивно они могут выполнять всё то же, что и изометрические преобразования, плюс масштабирование. Математически они обозначаются так:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} SR & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $

$ S = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix}$

Преобразования подобия сохраняют форму объектов, а значит, сохраняют:
Отношения длин отрезков
Величины углов

Важно отметить, что любое изометрическое преобразование является частным случаем преобразования подобия при $s = 1$. Однако обратное утверждение неверно.

Аффинные преобразования сохраняют:
Точки
Прямые линии
* Параллельность прямых

Для вектора $v$ аффинное преобразование $T$ определяется как: $T(v) = Av + t$, где $A$ — линейное преобразование пространства $R^n$

В однородных координатах аффинные преобразования записываются так:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Из этого уравнения видно, что все преобразования подобия (и, следовательно, изометрии) являются частным случаем аффинных преобразований.

Проективные преобразования (или гомографии) — это преобразования, которые переводят прямые в прямые, но не обязательно сохраняют параллельность.

В однородных координатах проективные преобразования представляются как:

$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ v & b \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

Это представление является обобщением аффинных преобразований за счёт добавления вектора $v$, который вводит дополнительные степени свободы.

Несмотря на то, что проективные преобразования не сохраняют параллельность, они сохраняют:
Коллинеарность точек (прямые переходят в прямые)
Перекрестное отношение четырёх коллинеарных точек.

Перекрестное отношение четырёх точек $P_1, P_2, P_3, P_4$, лежащих на одной прямой, вычисляется по формуле:

$cross\ ratio = \frac{||P_3 - P_1||\ ||P_4 - P_2||}{||P_3 - P_2||\ ||P_4 - P_1||}$ (1)

Доказательство инвариантности перекрестного отношения при проективных преобразованиях предлагается выполнить в качестве учебного упражнения.

2. Точки и прямые в бесконечности

Прямые играют важную роль в определении структуры изображений, поэтому важно понимать их представление как в 2D, так и в 3D пространстве.

Прямая на плоскости может быть представлена однородным вектором $\ell = \begin{bmatrix} a & b & c \end{bmatrix}^T$.

Отношение $-\frac{a}{b}$ определяет наклон прямой, а отношение $-\frac{c}{b}$ — точку пересечения с осью $y$.

Для любой точки, лежащей на прямой, справедливо уравнение:

$\forall p = \begin{bmatrix} x \\ y \end{bmatrix} \in \ell, \quad \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0$ (2)

Пересечение прямых
В общем случае две прямые $\ell$ и $\ell'$ пересекаются в точке $x$, которая определяется как векторное произведение этих прямых.

• Доказательство: если две прямые пересекаются, точка пересечения $x$ должна лежать на обеих прямых. Следовательно, $x^T\ell = 0$ и $x^T\ell' = 0$. Если мы положим $x = \ell \times \ell'$, то по определению векторного произведения вектор $x$ будет ортогонален обоим векторам $\ell$ и $\ell'$.

Параллельные прямые
В школьной геометрии считается, что параллельные прямые не пересекаются. Однако в однородных координатах можно сказать, что они пересекаются в бесконечности.

Рассмотрим две параллельные прямые $\ell$ и $\ell'$. Когда прямые параллельны, их наклоны равны: $\frac{a}{b} = \frac{a'}{b'}$. Если вычислить точку пересечения в однородных координатах, получим:

$\ell \times \ell' \propto \begin{bmatrix} b \\ -a \\ 0 \end{bmatrix} = x_\infty$ (3)

Это подтверждает, что параллельные прямые пересекаются в бесконечности. Точка пересечения параллельных прямых в бесконечности называется идеальной точкой.

В однородных координатах идеальная точка в бесконечности представляется как:

$\begin{bmatrix} x \ y \ 0 \end{bmatrix}^T$

Свойство идеальных точек Все параллельные прямые с одинаковым наклоном $-\frac{a}{b}$ проходят через идеальную точку:

$\ell^T x_\infty = \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} b \\ -a \\ 0 \end{bmatrix} = 0$ (4)

Бесконечно удалённые точки позволяют определить прямую в бесконечности. Рассмотрим несколько пар параллельных прямых. Каждая пара пересекается в своей точке бесконечности $x_{\infty,i}$. Прямая $\ell_\infty$, проходящая через все эти точки, должна удовлетворять условию:

$\forall i, \ell_\infty^T x_{\infty,i} = 0$

Рисунок 1: Точки в бесконечности образуют прямые в бесконечности

Такая прямая имеет вид $\ell_\infty = \begin{bmatrix} 0 & 0 & c \end{bmatrix}^T$. Поскольку $c$ — произвольное значение, можно принять:

$\ell_\infty = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^T$

Проективное преобразование точки в бесконечности:

При применении проективного преобразования $H$ к точке в бесконечности $p_\infty$ получаем:

$p' = Hp_\infty = \begin{bmatrix} A & t \\ v & b \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix}$ (5)

Заметим, что последний элемент $p'$ может стать ненулевым. Это означает, что проективное преобразование обычно переводит точки в бесконечности в точки, которые уже не находятся в бесконечности. Т.е. имеют конечные евклидовы координаты, пусть и за пределами изображения.

Аффинные преобразования ведут себя иначе и всегда переводят точку из бесконечности в бесконечность:

$p' = Hp_\infty = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p'_x \\ p'_y \\ 0 \end{bmatrix}$ (6)

Преобразование прямых

При применении проективного преобразования $H$ к прямой $\ell$ получаем новую прямую $\ell'$. Все точки $x$, лежащие на прямой, должны удовлетворять условию $x^T\ell = 0$. В преобразованном пространстве прямые переходят в прямые, то есть $x'^T\ell' = 0$. Используя свойство тождественного преобразования, получаем:

$x^TI\ell = x^TH^TH^{-T}\ell = 0$

При применении проективного преобразования к прямой происходит преобразование всех точек, лежащих на ней. Если $x$ — точка исходной прямой, то после преобразования получаем:

$x' = Hx$

Используя это преобразование, можно записать:

$x^TH^TH^{-T}\ell = x'^T\ell'$,

откуда следует, что проективное преобразование прямой имеет вид:

$\ell' = H^{-T}\ell$

Важные выводы:
При проективном преобразовании прямая в бесконечности не обязательно переходит в другую прямую в бесконечности
В отличие от этого, аффинные преобразования сохраняют прямые в бесконечности, переводя их в прямые в бесконечности.

Эти свойства имеют важное значение для понимания того, как различные типы преобразований влияют на структуру изображения и геометрию сцены. Особенно это касается работы с бесконечно удалёнными точками и прямыми, которые играют ключевую роль в проективной геометрии и компьютерном зрении.

Таким образом, при работе с проективными преобразованиями необходимо учитывать, что они могут существенно изменять геометрию сцены, в том числе расположение прямых и точек в бесконечности, в то время как аффинные преобразования сохраняют некоторые геометрические свойства.

3. Точки и линии схода

В трёхмерном пространстве вводится понятие плоскости, которая представляется вектором $\begin{bmatrix} a & b & c & d \end{bmatrix}^T$. Здесь $(a, b, c)$ образуют вектор нормали, а $d$ — расстояние от начала координат до плоскости в направлении этого вектора. Формально плоскость определяется как множество точек $x$, удовлетворяющих уравнению:

$x^T \begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} = ax_1 + bx_2 + cx_3 + d = 0$ (7)

Прямые в 3D определяются как пересечение двух плоскостей. Они имеют четыре степени свободы (точка пересечения и наклоны в трёх измерениях).

Точки в бесконечности в 3D определяются как точки пересечения параллельных прямых. При проективном преобразовании таких точек получается точка схода $p_\infty$ на плоскости изображения.

Существует полезное соотношение между параллельными прямыми в 3D, их точкой схода на изображении и параметрами камеры $K$, $R$, $T$.

Пусть $d = (a, b, c)$ — направление набора параллельных прямых в системе координат камеры. Тогда точка схода $v$ определяется как:

$v = Kd$ (8)

Отсюда можно выразить направление $d$:

$d = \frac{K^{-1}v}{|K^{-1}v|}$ (9)

Линия горизонта (или линия схода) $l_{horiz}$ — это проекция линии в бесконечности на плоскость изображения. Она проходит через соответствующие точки схода на изображении и вычисляется по формуле:

$l_{horiz} = H^{-T}P l_\infty$ (10)

Точки и линии схода являются важными инструментами для анализа структуры сцены и определения параметров камеры по изображению, т.к. они позволяют восстанавливать трёхмерную геометрию по двумерной проекции.

Линия горизонта позволяет нам интуитивно определять свойства изображения, которые могут быть неочевидны с математической точки зрения. Например, линии на земле не выглядят параллельными на изображении (как показано на рисунке 2), но интуитивно мы все же понимаем, что в трёхмерном пространстве они параллельны.

Линия горизонта позволяет вычислять важные характеристики сцены. Существует интересное соотношение между нормалью $n$ плоскости в 3D и соответствующей линией горизонта $l_{horiz}$ на изображении:

$n = K^Tl_{horiz}$ (11)

Это означает, что если мы можем определить линию горизонта, связанную с плоскостью, и знаем внутренние характеристики камеры $K$, мы можем оценить ориентацию этой плоскости.

Теперь давайте рассмотрим понятие плоскость в бесконечности.

Рисунок 3: Плоскость в бесконечности

Эта плоскость определяется набором из двух или более линий схода. В однородных координатах плоскость описывается вектором:

$Π_\infty = \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}^T$

Плоскость в бесконечности поможет нам понять важное свойство, связывающее линии и плоскости в 3D с соответствующими точками и линиями схода на плоскости изображения.

Рисунок 4: Определение угла между линиями

Пусть две пары параллельных линий в 3D имеют направления $d_1$ и $d_2$, связанные с точками в бесконечности $x_{1,\infty}$ и $x_{2,\infty}$. Пусть $v_1$ и $v_2$ — соответствующие точки схода. Тогда угол $θ$ между $d_1$ и $d_2$ определяется по формуле:

$\cos θ = \frac{d_1 \cdot d_2}{|d_1||d_2|} = \frac{v_1^T \omega v_2}{\sqrt{v_1^T \omega v_1} \sqrt{v_2^T \omega v_2}}$ (12)

где $\omega = (KK^T)^{-1}$.

Матрица $\omega$ определяется через матрицу камеры $K$ следующим образом:

$\omega = (K K^T)^{-1}$

Эта матрица имеет важные свойства:

1. Симметричность: матрица $\omega$ является симметричной, так как $K K^T$ — симметричная матрица, а обратная к симметричной матрице также симметрична

2. Связь с параметрами камеры: содержит информацию о внутренних параметрах камеры, зависит от фокусных расстояний, координат главной точки и коэффициента скоса (skew).

3. При стандартных предположениях о камере (нулевой скос, квадратные пиксели) матрица $\omega$ имеет вид:

$\omega = \begin{bmatrix} \omega_1 & 0 & \omega_4 \\ 0 & \omega_1 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6 \end{bmatrix}$

Матрица $\omega$ определяется с точностью до масштабного множителя, что влияет на количество независимых переменных при решении системы уравнений. Это свойство учитывается при калибровке камеры и восстановлении 3D-структуры сцены.

Это соотношение показывает, как можно определить угол между направлениями в пространстве, используя только точки схода на изображении и параметры камеры.

И наконец, расширим рассмотренную концепцию на случай трёхмерных плоскостей, чтобы установить связь между различными плоскостями в 3D пространстве.

Для любой плоскости мы можем:
Вычислить соответствующую линию горизонта $l_{horiz}$
Определить нормаль к плоскости $n = K^\ l_{horiz}$

Угол $\theta$ между двумя плоскостями можно определить через угол между их нормалями $n_1$ и $n_2$. Рассмотрим две плоскости с линиями горизонта $l_1$ и $l_2$ соответственно. Угол между нормалями этих плоскостей определяется формулой:

$\cos \theta = \frac{n_1 \cdot n_2}{|n_1||n_2|} = \frac{l_1^T \omega^{-1} l_2}{\sqrt{l_1^T \omega^{-1} l_1} \sqrt{l_2^T \omega^{-1} l_2}}$ (13)

Таким образом, используя линии горизонта и параметры камеры, мы можем восстанавливать пространственные отношения между плоскостями в сцене, что является важным инструментом в компьютерном зрении и трёхмерной реконструкции.

4. Алгоритм калибровки камеры и измерения углов

Рассмотрим пример решения задачи калибровки камеры по одной фотографии. Для этого нам понадобится изображение трёхмерного мира, на котором мы можем выполнить следующие операции:
Определить три плоскости и на каждой из этих плоскостей пару параллельных линий
Идентифицировать точки схода $v_1$ $v_2$ и $v_3$
* Использовать априорное знание и том, что плоскости перпендикулярны в 3D пространстве.

Рисунок 5: Точки схода на перпендикулярных плоскостях

Из уравнения (12) мы знаем, что для перпендикулярных плоскостей выполняется соотношение $v_1\omega v_2 = 0$.

Если мы имеем три точки схода для трех взаимно перпендикулярной плоскости, то получаем систему:

$v_1\omega v_2 = 0$
$v_1\omega v_3 = 0$
$v_2\omega v_3 = 0$

При предположении об отсутствии скоса камеры и квадратных пикселях, мы можем решить эту систему относительно элементов матрицы $\omega_1, \omega_4, \omega_5, \omega_6$ (с точностью до масштаба).

Зная матрицу $\omega$, можно вычислить элементы матрицы камеры $K$ с помощью разложения Холецкого.

Таким образом, мы выполняем калибровку камеры всего по одному изображению. После определения $K$ мы можем восстановить 3D-геометрию сцены, вычислить ориентацию всех идентифицированных плоскостей, а также получить обширную информацию о снимаемой сцене с точностью до масштабного коэффициента.

Калибровка камеры

Чтобы точно знать преобразование из реального трёхмерного мира в цифровые изображения, необходимо заранее знать многие внутренние параметры камеры. Если у нас есть произвольная камера, мы можем как иметь доступ к этим параметрам, так и не иметь его. Однако у нас есть доступ к изображениям, которые делает камера.

Возникает вопрос: можем ли мы найти способ вывести эти параметры из изображений? Эта задача оценки внешних и внутренних параметров камеры известна как калибровка камеры.

Калибровка камеры — это фундаментальный процесс в компьютерном зрении и обработке изображений, который позволяет нам переходить от наблюдаемых пикселей к реальным координатам в пространстве.

Рисунок 1: Пример калибровочной установки

Процесс калибровки камеры заключается в определении внутренней матрицы камеры $K$ и внешних параметров $R$, $T$ из уравнения (1).

$P' = K \begin{bmatrix} R & T \end{bmatrix} P_w = MP_w$ (1)

Рассмотрим этот процесс в контексте калибровочной установки, подобной показанной на рисунке 1.

Калибровочная установка обычно состоит из простого шаблона (например, шахматной доски) с известными размерами. Кроме того, установка определяет нашу мировую систему координат с началом $O_w$ и осями $i_w$, $j_w$, $k_w$.

Из известного шаблона мы получаем точки в мировой системе координат $P_1, ..., P_n$. Найдя эти точки на изображении, полученном с камеры, мы получаем соответствующие точки изображения $p_1, ..., p_n$.

Мы составляем линейную систему уравнений из $n$ соответствий, таких что для каждого соответствия $P_i$, $p_i$ и матрицы камеры $M$, строки которой $m_1$, $m_2$, $m_3$:

$p_i = \begin{pmatrix} u_i \\ v_i \end{pmatrix} = MP_i = \begin{pmatrix} \frac{m_1P_i}{m_3P_i} \\ \frac{m_2P_i}{m_3P_i} \end{pmatrix}$ (2)

Уравнение (2) даёт нам два ограничения для нахождения неизвестных параметров, содержащихся в $m$.

Мы знаем, что матрица камеры имеет 11 неизвестных параметров (6 внешних и 5 внутренних). Это означает, что нам нужно как минимум 6 соответствий для решения. Однако в реальном мире мы часто используем больше соответствий, поскольку измерения часто зашумлены.

Для каждой точки $P_i$ мы можем вывести пару уравнений, связывающих координаты на плоскости $u_i, v_i$ с 3D координатами:

$u_i(m_3P_i) − m_1P_i = 0$
$v_i(m_3P_i) − m_2P_i = 0$

При наличии $n$ таких соответствующих точек вся линейная система уравнений принимает вид:

$u_1(m_3P_1)−m_1P_1 = 0$
$v_1(m_3P_1)−m_2P_1 = 0$
...
$u_n(m_3P_n)−m_1P_n = 0$
$v_n(m_3P_n)−m_2P_n = 0$

Мы можем вынести вектора $m_1 , m_2, m_3$ и представить эту систему уравнений в виде матричного произведения:

$\begin{bmatrix} P_1^T & 0^T & -u_1P_1^T \\ 0^T & P_1^T & -v_1P_1^T \\ \vdots & \vdots & \vdots \\ P_n^T & 0^T & -u_nP_n^T \\ 0^T & P_n^T & -v_nP_n^T \end{bmatrix} \begin{bmatrix} m_1^T \\ m_2^T \\ m_3^T \end{bmatrix} = Pm = 0$ (3)

Когда $2n > 11$, наша однородная линейная система является переопределённой. Для такой системы $m = 0$ всегда является тривиальным решением. Более того, даже если существует ненулевое решение $m$, то для любого $\rho \in \mathbb{R}$, $km$ также будет решением.

Поэтому для ограничения решения мы выполняем следующую минимизацию:

$\min_{m} |Pm|^2 \quad \text{при условии} \quad |m|^2 = 1$ (4)

Для решения этой задачи минимизации используется сингулярное разложение. Если обозначить $P = UDV^T$, то решение задачи минимизации заключается в том, чтобы установить $m$ равным последнему столбцу матрицы $V$. Обоснование данного решения выходит за рамки этого курса. Для более подробного изучения вы можете обратиться к разделу 5.3 книги Hartley & Zisserman стр. 592–593.

В этом разделе вы найдёте:
- Математическое обоснование метода
- Подробное доказательство решения
- Дополнительные технические детали

После преобразования вектора $m$ в матрицу $M$ мы хотим явно найти внешние и внутренние параметры камеры.

C помощью SVD мы вычислили матрицу $M$, с точностью до масштабного множителя $\rho$.

$\rho M = \begin{bmatrix} \alpha r_1^T - \alpha \cot \theta r_2^T + c_x r_3^T & \alpha t_x - \alpha \cot \theta t_y + c_x t_z \\ \frac{\beta}{\sin \theta} r_2^T + c_y r_3^T & \frac{\beta}{\sin \theta} t_y + c_y t_z \\ r_3^T & t_z \end{bmatrix}$ (5)

где $r_1^T$, $r_2^T$, и $r_3^T$ — это три строки матрицы вращения $R$.

Разделим на скаляр $\rho$ и обозначим первый столбец как матрицу $A$, а второй столбец как вектор $b$:

$M = \frac{1}{\rho} \begin{bmatrix} \alpha r_1^T - \alpha \cot \theta r_2^T + c_x r_3^T & \alpha t_x - \alpha \cot \theta t_y + c_x t_z \\ \frac{\beta}{\sin \theta} r_2^T + c_y r_3^T & \frac{\beta}{\sin \theta} t_y + c_y t_z \\ r_3^T & t_z \end{bmatrix} = \begin{bmatrix} A & b \end{bmatrix} = \begin{bmatrix} a_1^T & b_1 \\ a_2^T & b_2 \\ a_3^T & b_3 \end{bmatrix}$

Теперь мы можем вычислить внутренние параметры камеры через элементы известной матрицы $M$, она же $A$ и $b$: (6)

Масштабный множитель:
$\rho = \pm \frac{1}{|a_3|}$

Координаты главной точки:
$c_x = \rho^2 (a_1 \cdot a_3)$
$c_y = \rho^2 (a_2 \cdot a_3)$

Угол скоса:
$\theta = \cos^{-1} \left( -\frac{(a_1 \times a_3) \cdot (a_2 \times a_3)}{|a_1 \times a_3| \cdot |a_2 \times a_3|} \right)$

Масштабные коэффициенты:
$\alpha = \rho^2 |a_1 \times a_3| \sin \theta$
$\beta = \rho^2 |a_2 \times a_3| \sin \theta$

Формулы для вычисления внешних параметров (7)

Матрица вращения:
$r_1 = \frac{a_2 \times a_3}{|a_2 \times a_3|}$
$r_2 = r_3 \times r_1$
$r_3 = \rho a_3$

Вектор переноса:
$T = \rho K^{-1} b$

При подготовке данных для процедуры калибровки важно учитывать особые случаи, при которых процесс может дать некорректные результаты. Вырожденные конфигурации возникают, когда точки $P_i$ располагаются в одной плоскости или лежат на кривой пересечения двух квадрик. В таких случаях система уравнений становится неразрешимой, что приводит к невозможности корректного определения параметров камеры. Чтобы избежать подобных проблем, следует тщательно подходить к процессу калибровки. Необходимо использовать точки с различной глубиной расположения, обеспечивать разнообразие положений калибровочной мишени в пространстве и внимательно следить за распределением точек. Важно также проверять качество получаемых данных и анализировать корректность результатов на тестовых наборах. Для более глубокого понимания теоретических аспектов рекомендуется обратиться к разделу 1.3.1 учебника Forsyth & Ponce, где подробно рассматриваются вырожденные конфигурации и методы их предотвращения.

2. Компенсация искажений при калибровке камеры

До этого момента мы рассматривали идеальные линзы, свободные от любых искажений. Однако в реальности объективы могут отклоняться от прямолинейной проекции, что требует применения более сложных методов обработки. В этом разделе мы кратко рассмотрим подходы к работе с искажениями.

Благодаря физической симметрии линзы радиальные искажения тоже обладают симметрией. Для моделирования радиальных искажений используется изотропное преобразование $Q$:

$Q P_i = \begin{bmatrix} q_1 \\ q_2 \\ q_3 \end{bmatrix} P_i = \begin{bmatrix} \frac{1}{\lambda} & 0 & 0 \\ 0 & \frac{1}{\lambda} & 0 \\ 0 & 0 & 1 \end{bmatrix} M P_i = \begin{bmatrix} u_i \\ v_i \end{bmatrix} = p_i$ (8)

Переписав в систему векторных уравнений, получаем:

$u_i q_3 P_i = q_1 P_i$
$v_i q_3 P_i = q_2 P_i$

Однако такая система перестаёт быть линейной, и для её решения требуются методы нелинейной оптимизации, которые подробно рассматриваются в разделе 22.2 учебника Forsyth & Ponce.

Упростить процесс нелинейной оптимизации при калибровке можно, сделав определённые допущения. В случае радиальных искажений важно отметить, что соотношение между координатами $u_i$ и $v_i$ остаётся неизменным. Это соотношение можно вычислить следующим образом:

$\frac{u_i}{v_i} = \frac{\frac{m_1P_i}{m_3P_i}}{\frac{m_2P_i}{m_3P_i}} = \frac{m_1P_i}{m_2P_i}$ (18)

При наличии $n$ соответствий мы можем составить систему линейных уравнений следующего вида:

$v_1(m_1P_1) - u_1(m_2P_1) = 0$
$\vdots$
$v_n(m_1P_n) - u_n(m_2P_n) = 0$

Эта система может быть представлена в виде матрично-векторного произведения, решаемого с помощью сингулярного разложения (SVD):

$L n = \begin{bmatrix} v_1P_1^T & -u_1P_1^T \\ \vdots & \vdots \\ v_nP_n^T & -u_nP_n^T \end{bmatrix} \begin{bmatrix} m_1^T \\ m_2^T \end{bmatrix}$ (19)

После оценки векторов $m_1$ и $m_2$ вектор $m_3$ может быть выражен как нелинейная функция от $m_1$, $m_2$ и $\lambda$. Это приводит к необходимости решения задачи нелинейной оптимизации, которая значительно проще исходной задачи оценки элементов матрицы $Q$.

Процесс решения включает следующие этапы:

1. Формирование матрицы $L n$ на основе известных соответствий между точками
2. Применение SVD для нахождения $m_1$ и $m_2$
3. Вычисление $m_3$ через нелинейную зависимость

Используем условие ортогональности:

$m_1 \cdot m_3 = 0$ и $m_2 \cdot m_3 = 0$

Учитываем нормировку:

$|m_3| = 1$

Вводим зависимость от параметра $\lambda$, итоговая формула для вычисления $m_3$ имеет вид:

$m_3 = \frac{m_1 \times m_2}{|m_1 \times m_2|} \cdot g(\lambda)$

где $g(\lambda)$ — некоторая функция от параметра $\lambda$, зависящая от конкретной модели искажений.

Вид функции $g(\lambda)$ зависит от требуемой точности модели.

Полиномиальная модель общего вида:

$g(\lambda) = 1 + k_1\lambda^2 + k_2\lambda^4 + k_3\lambda^6 + ...$

где $k_1, k_2, k_3$ — коэффициенты радиальных искажений.

На практике используют вычислительно несложные модели:

$g(\lambda) = 1 + k_1\lambda^2$

или

$g(\lambda) = 1 + k_1\lambda^2 + k_2\lambda^4$

Модель Брауна включает как радиальные, так и тангенциальные искажения:

$x_{distorted} = x(1 + k_1r^2 + k_2r^4) + 2p_1xy + p_2(r^2 + 2x^2)$

$y_{distorted} = y(1 + k_1r^2 + k_2r^4) + p_1(r^2 + 2y^2) + 2p_2xy$

где $r^2 = x^2 + y^2$

Резюме

Калибровка камеры — это комплексный процесс определения внутренних и внешних параметров оптической системы для точного преобразования координат между трёхмерным пространством и двумерным изображением. В основе калибровки лежит использование калибровочной мишени с известными координатами, что позволяет установить соответствие между мировыми и экранными координатами. Процесс включает определение матрицы камеры, которая содержит информацию о фокусном расстоянии, координатах главной точки и коэффициентах искажения.

Важным этапом является учёт искажений, которые неизбежно присутствуют в реальных объективах. Для их компенсации применяются специальные математические модели, чаще всего основанные на полиномиальных функциях радиальных искажений. При калибровке необходимо избегать вырожденных конфигураций, когда точки располагаются в одной плоскости, что делает невозможным корректное определение параметров. Практическая реализация требует достаточного количества калибровочных изображений с разнообразным расположением мишени относительно камеры. После завершения калибровки получается набор параметров, позволяющий компенсировать искажения и восстанавливать пространственные координаты по изображениям с точностью до удаления $z$.

Качество калибровки напрямую влияет на точность последующих измерений и является критически важным этапом в системах компьютерного зрения и машинного обучения.

1. Введение

Камера является одним из важнейших инструментов в компьютерном зрении. Это механизм, с помощью которого мы можем фиксировать окружающий мир и использовать получаемые результаты — фотографии — для различных приложений. Поэтому один из фундаментальных вопросов трехмерного компьютерного зрения звучит так: как мы можем смоделировать камеру?

2. Камера-обскура

Камера-обскура — это простейшая система, которая позволяет фиксировать изображение объекта или сцены в трёхмерном мире. Такая система может быть создана путём размещения преграды с небольшим отверстием (апертурой) между трёхмерным объектом и фотоплёнкой или светочувствительным сенсором.

Рисунок 1: Модель камеры обскуры

Как показано на рисунке 1, каждая точка на трёхмерном объекте испускает множество световых лучей во все стороны. Без преграды каждая точка на плёнке подвергалась бы воздействию световых лучей, исходящих от каждой точки трёхмерного объекта. Благодаря наличию преграды через отверстие проходит только один (или несколько) из этих лучей света и попадает на плёнку.

Таким образом, мы можем установить взаимно-однозначное соответствие между точками на трёхмерном объекте и точками на плёнке. В результате плёнка получает «изображение» трёхмерного объекта посредством такого отображения. Эта простая модель известна как модель камеры-обскуры.

Рисунок 2: Формальная модель модели камеры-обскуры

Более формальное построение камеры-обскуры показано на рисунке 2. В этой конструкции плёнка обычно называется плоскостью изображения или сетчаткой. Отверстие называется точечным отверстием O или центром камеры. Расстояние между плоскостью изображения и точечным отверстием O называется фокусным расстоянием f.

Иногда плоскость сетчатки размещается между точкой O и трёхмерным объектом на расстоянии f от O. В этом случае она называется виртуальной плоскостью изображения или виртуальной плоскостью сетчатки. Важно отметить, что проекция объекта на плоскость изображения и изображение объекта на виртуальной плоскости изображения идентичны с точностью до масштабного (подобного) преобразования.

Теперь рассмотрим, как использовать камеры-обскуры. Пусть P = [x y z]ᵀ — точка на некотором трёхмерном объекте, видимом для камеры-обскуры. Точка P будет отображена или спроецирована на плоскость изображения Π', в результате чего получится точка P' = [x' y']ᵀ.

Аналогично, само точечное отверстие может быть спроецировано на плоскость изображения, что даст новую точку C'. Здесь мы можем определить систему координат [i j k], центрированную в точке отверстия O, так что ось k перпендикулярна плоскости изображения и направлена к ней. Эта система координат часто известна как система отсчёта камеры или система координат камеры.

Линия, определяемая точками C' и O, называется оптической осью системы камеры.

Напомним, что точка $P_0$ получается в результате проекции трёхмерной точки $P$ на плоскость изображения $Π'$. Следовательно, если мы выведем соотношение между трёхмерной точкой $P$ и точкой $P'$ на плоскости изображения, мы сможем понять, как трёхмерный мир отображается на снимке, сделанном камерой-обскурой.

Обратите внимание, что треугольник $P' C'O$ подобен треугольнику, образованному точками $P$, $O$ и $(0, 0, z)$. Используя теорему о подобных треугольниках, мы получаем:

$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{fx}{z} \\ \frac{fy}{z} \end{pmatrix}$ (1)

Важно отметить, что в этой модели камеры-обскуры мы делаем одно существенное допущение: апертура (отверстие) считается одной точкой. Однако в большинстве реальных ситуаций мы не можем предполагать, что апертура может быть бесконечно малой. Возникает вопрос: как влияет изменение размера апертуры на результат?

Рисунок 3: Влияние размера апертуры на изображение

При уменьшении размера апертуры изображение становится более резким, но более тёмным.

По мере увеличения размера апертуры количество световых лучей, проходящих через преграду, соответственно возрастает. При большем количестве проходящих лучей каждая точка на плёнке может подвергаться воздействию световых лучей от нескольких точек в трёхмерном пространстве, что приводит к размытию изображения.

Хотя может показаться заманчивым сделать апертуру как можно меньше, следует помнить, что меньший размер апертуры пропускает меньше световых лучей, в результате чего изображение получается более чётким, но более тёмным.

Таким образом, мы приходим к фундаментальной проблеме, возникающей при использовании камеры-обскуры: возможно ли создать камеру, которая делает одновременно чёткие и яркие изображения?

3. Камеры и линзы

В современных камерах указанное противоречие между резкостью и яркостью изображения решается с помощью линз — устройств, способных фокусировать или рассеивать свет.

Если заменить отверстие (апертуру) камеры-обскуры на линзу, которая правильно расположена и имеет подходящий размер, то она будет обладать следующим свойством: все световые лучи, испускаемые некоторой точкой $P$, преломляются линзой таким образом, что они сходятся в одной точке $P'$.

Рисунок 4: Схема простой модели линзы

На рисунке 4 показано, как лучи от верхней точки дерева хорошо сходятся на плёнке. Однако точка, находящаяся на другом расстоянии от линзы, приводит к тому, что лучи не сходятся идеально на плёнке.

Благодаря линзе проблема блокировки большинства световых лучей из-за малого отверстия устраняется (см. рисунок 4). Однако важно отметить, что это свойство выполняется не для всех точек трёхмерного пространства, а только для определённой точки $P$.

Рассмотрим другую точку $Q$, которая находится ближе или дальше от плоскости изображения, чем точка $P$. Соответствующая проекция на изображение будет размытой или не в фокусе. Таким образом, у линз есть определённое расстояние, на котором объекты находятся «в фокусе». Эффективный диапазон, в пределах которого камеры могут делать чёткие снимки называется глубина резкости.

Рисунок 5: Фокусировка световых лучей с помощью линзы

На данном рисунке демонстрируется, как линза фокусирует световые лучи, параллельные оптической оси, в фокусе (фокальной точке). Эта схема также иллюстрирует модель параксиального преломления — упрощённую модель, которая помогает установить взаимосвязь между точками на плоскости изображения и объектами в трёхмерном пространстве для камер с линзами.

Параксиальное преломление — это приближение, используемое в оптике, которое позволяет:
- точно рассчитывать траектории световых лучей;
- определять положение точек в пространстве;
- вычислять параметры фокусировки;
- моделировать работу оптических систем.

Такая модель является фундаментальной для понимания принципов работы современных камер и систем компьютерного зрения.

Объективы камер обладают ещё одним важным свойством: они фокусируют все световые лучи, движущиеся параллельно оптической оси, в одну точку, известную как фокусная точка (см. рисунок 5). Расстояние между фокусной точкой и центром линзы называется фокусным расстоянием $f$.

Кроме того, световые лучи, проходящие через центр линзы, не отклоняются. Благодаря этому мы можем построить конструкцию, аналогичную модели камеры-обскуры, которая связывает точку $P$ в трёхмерном пространстве с соответствующей точкой $P'$ на плоскости изображения:

$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} z' \frac{x}{z} \\ z' \frac{y}{z} \end{pmatrix}$ (2)

Важно отметить следующие различия между моделями:
- В модели камеры-обскуры $z' = f$
- В модели с линзой $z' = f + z_0$

Данное соотношение основано на параксиальном приближении (или предположении о «тонкой линзе»), а такая модель называется моделью параксиального преломления. Подробное доказательство этой модели выходит за рамки данного курса.

Рисунок 6: Подушкообразное и бочкообразное искажение изображения

Поскольку модель параксиального преломления использует приближение тонкой линзы, может возникать ряд аберраций. Наиболее распространённой из них является радиальное искажение, которое приводит к уменьшению или увеличению увеличения изображения в зависимости от расстояния до оптической оси.

Мы классифицируем радиальное искажение следующим образом:
- Подушкообразное искажение — когда увеличение возрастает
- Бочкообразное искажение — когда увеличение уменьшается.

Радиальное искажение возникает из-за того, что различные участки линзы имеют разные фокусные расстояния. Это явление наглядно показано на рисунке 6, где можно увидеть, как эти типы искажений влияют на конечное изображение.

Такие искажения особенно заметны: - По краям кадра - При использовании широкоугольных объективов - В системах компьютерного зрения, где важна точность геометрических измерений

4. Матричная модель камеры

В этом разделе мы рассмотрим детали параметров, которые необходимо учитывать при моделировании проекции из трёхмерного пространства на известные нам цифровые изображения. Все полученные результаты будут использовать модель камеры-обскуры, но они также применимы и к модели параксиального преломления.

Как обсуждалось ранее, точка $P$ в трёхмерном пространстве может быть отображена (или спроецирована) в двумерную точку $P'$ на плоскости изображения $Π'$. Такое отображение $R^3 → R^2$ называется проективным преобразованием.

Однако такая проекция трёхмерных точек на плоскость изображения не соответствует напрямую тому, что мы видим в реальных цифровых изображениях по нескольким причинам:

1. Точки в цифровых изображениях, как правило, находятся в другой системе отсчёта, чем точки в плоскости изображения.
2. Цифровые изображения разделены на дискретные пиксели, тогда как точки в плоскости изображения являются непрерывными.
3. Физические датчики могут вносить нелинейные искажения в отображение.

Чтобы учесть эти различия, мы введём ряд дополнительных преобразований, которые позволят нам отображать любую точку из трёхмерного мира в координаты пикселей.

Таким образом, нам необходимо:
- Учесть различия в системах координат;
- Преобразовать непрерывные координаты в дискретные пиксельные;
- Компенсировать возможные искажения сенсора.

Матричная модель камеры описывает набор важных параметров, влияющих на то, как точка мира $P$ отображается в координаты изображения $P'$. Как следует из названия, эти параметры представлены в матричной форме.

Рассмотрим основные параметры:

Параметры $c_x$ и $c_y$ описывают разницу между координатами плоскости изображения и цифровыми координатами изображения через перенос.
- Координаты плоскости изображения имеют начало координат $C_0$ в центре изображения, где ось $k$ пересекает плоскость изображения.
- Цифровые координаты изображения обычно имеют начало в левом нижнем углу изображения.
- Таким образом, 2D точки на плоскости изображения и 2D точки в цифровом изображении смещаются на вектор переноса $\begin{pmatrix} c_x \\ c_y \end{pmatrix}^T$.

С учётом этого изменения систем координат отображение теперь выглядит так:

$P' = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \frac{f}{z}x + c_x \\ \frac{f}{z}y + c_y \end{pmatrix}$ (3)

Второй важный эффект — это то, что точки в цифровых изображениях выражаются в пикселях, в то время как точки на плоскости изображения представлены в физических измерениях (например, сантиметрах).

Для учёта этого изменения единиц измерения необходимо ввести два новых параметра $k$ и $l$. Эти параметры имеют размерность [пиксель на сантиметр], соответствуют изменению единиц измерения по двум осям плоскости изображения. Важно отметить, что $k$ и $l$ могут быть разными, поскольку соотношение сторон пикселя не обязательно равно единице. Если $k = l$, мы говорим, что камера имеет квадратные пиксели. Мы модифицируем наше предыдущее отображение следующим образом:

$P_0 = \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} f k \frac{x}{z} + c_x \\ f l \frac{y}{z} + c_y \end{pmatrix} = \begin{pmatrix} \alpha\frac{x}{z} + c_x \\ \beta\frac{y}{z} + c_y \end{pmatrix}$ (4)

где
$\alpha = f \cdot k$
$\beta = f \cdot l$
$f$ — фокусное расстояние в мм,
$k$ — размер пикселя по оси x, пикс/мм.
$l$ — размер пикселя по оси x, пикс/мм.

Сокращение размерностей приводит к тому, что параметры $\alpha$ и $\beta$ выражаются в пикселях.
Это логично, так как коэффициенты связывают физические измерения (метры) с дискретными единицами цифрового изображения (пиксели).

Геометрический смысл состоит в том, сколько в пикселях будет объект, размер которого на плоскости проекции равен фокусному расстоянию камеры.

Таким образом, измерение $\alpha$ и $\beta$ в пикселях является необходимым для:
- Точного проецирования точек;
- Корректной калибровки камеры;
- Работы алгоритмов обработки изображений;
- Взаимодействия между физическим и цифровым пространством.

5. Однородные координаты

Теперь рассмотрим вопрос: существует ли линейный способ представления проецирования $P \rightarrow P'$?

Линейное преобразование на практике является более удобным, т.к. его можно представить как произведение входного вектора $P$ на некоторую матрицу. Из уравнения (4) видно, что проецирование $P \rightarrow P'$ не является линейным, поскольку операция включает деление на один из входных параметров, а именно на $z$. Тем не менее, представление этого проецирования в виде произведения вектора на матрицу возможно. Решение заключается в использовании однородных координат.

Рассмотрим этот подход:

1. Введение новой координаты:
   Любая точка на плоскости $P' = (x', y')$ преобразуется в $(x', y', 1)$
   Любая точка в трехмерном пространстве $P = (x, y, z)$ преобразуется в $(x, y, z, 1)$

Такое расширенное пространство называется системой однородных координат.

1. Преобразование координат:
   Для преобразования евклидова вектора $(v_1, ..., v_n)$ в однородные координаты мы просто добавляем 1 в новое измерение, получая $(v_1, ..., v_n, 1)$
   Важно отметить: равенство между вектором и его однородными координатами выполняется только когда последняя координата равна единице
   При обратном преобразовании из произвольных однородных координат $(v_1, ..., v_n, w)$ мы получаем евклидовы координаты $(\frac{v_1}{w}, ..., \frac{v_n}{w})$

Используя однородные координаты, мы можем сформулировать преобразование следующим образом:

$P'_h = \begin{bmatrix} \alpha x + c_x z \\ \beta y + c_y z \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P_h$ (5)

Преимущества использования однородных координат:
- Позволяют представить нелинейное преобразование в виде матричного умножения;
- Упрощают дальнейшие математические выкладки;
- Обеспечивают единый способ работы с проективными преобразованиями.

С этого момента будем работать преимущественно в однородных координатах, если не указано иное. Индекс $h$ опустим, подразумевая, что любая точка $P$ или $P'$ задана в однородных координатах.

Как видно из уравнения (5), мы можем представить связь между точкой в трёхмерном пространстве и её координатами изображения в виде матрично-векторного соотношения:

$P' = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P = MP$ (6)

где: - $M$ — матрица камеры
- $P$ — точка в однородных координатах трёхмерного пространства
- $P'$ — проекция точки на плоскость изображения

6. Внутренние параметры камеры

Важные параметры матрицы камеры:
- $\alpha$ и $\beta$ — масштабные коэффициенты в направлениях $x$ и $y$
- $c_x$ и $c_y$ — координаты главной точки (principal point)
- Последний столбец матрицы $M$ содержит нули, что характерно для проективных преобразований.

Давайте разберем это матричное разложение более подробно:

Мы можем представить преобразование в виде:

$P' = MP = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} I & 0 \end{bmatrix} P = K \begin{bmatrix} I & 0 \end{bmatrix} P$ (7)

где: - $P'$ — координаты точки на плоскости изображения
- $M$ — полная матрица преобразования
- $K$ — *матрица камеры- (внутренняя калибровка)
- $I$ — единичная матрица размером 3×3
- $0$ — нулевой вектор размером 3×1
- $P$ — координаты точки в пространстве в однородных координатах.

Рисунок 7: Проекция точки с помощью матрицы камеры

Матрица камеры $K$ имеет следующий вид:

$K = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix}$

где: - $\alpha$ и $\beta$ — масштабные коэффициенты, связанные с фокусным расстоянием
- $c_x$ и $c_y$ — координаты главной точки (principal point)
- Последняя строка [0 0 1] обеспечивает сохранение однородных координат

Такое разложение позволяет: - Выделить внутренние параметры камеры и работать с ними отдельно от внешних;
- Упрощать вычисления при работе с проективными преобразованиями;
- Более эффективно выполнять калибровку камеры;
- Разделять влияние различных параметров на процесс проецирования.

Матрица $K$ содержит всю необходимую информацию об внутренней калибровке камеры, что делает её ключевым элементом в задачах компьютерного зрения и обработки изображений.

Рисунок 8: Расположение главной точки С'

Полная матричная модель камеры $K$ содержит ключевые параметры, описывающие характеристики камеры и её модель, включая параметры $c_x$, $c_y$, $k$ и $l$, как обсуждалось ранее.

В текущей формулировке отсутствуют два важных параметра: * Скос (skewness) * Дисторсия (distortion)

Скос изображения возникает, когда система координат камеры имеет неточный угол между осями (отличающийся от 90 градусов). Большинство камер имеют нулевой скос, однако некоторое его значение может появиться из-за погрешностей при производстве сенсора.

Матрица камеры с учётом скоса имеет вид:

$K = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & -\alpha \cot \theta & c_x \\ 0 & \frac{\beta}{\sin \theta} & c_y \\ 0 & 0 & 1 \end{bmatrix}$ (8)

где:
- $\alpha$ и $\beta$ — масштабные коэффициенты
- $\theta$ — угол скоса
- $c_x$ и $c_y$ — координаты главной точки

В рамках данного курса мы рассматриваем матрицу камеры $K$ с 5 степенями свободы:
- 2 параметра для фокусного расстояния
- 2 параметра для смещения
- 1 параметр для скоса

Эти параметры называются внутренними параметрами камеры (intrinsic parameters), так как они:
- Уникальны для каждой конкретной камеры
- Связаны с её конструктивными особенностями
- Определяются при производстве

Важно отметить, что большинство методов компьютерного зрения игнорируют эффекты дисторсии, позволяя состедоточиться на 4 основных параметрах камеры.

7. Внешние параметры камеры

До сих пор мы описывали отображение точки $P$ из трёхмерной системы координат камеры в точку $P'$ на двумерной плоскости изображения, используя внутренние параметры камеры в матричной форме.

Однако возникает вопрос: что делать, если информация о трёхмерном мире представлена в другой системе координат? В этом случае необходимо добавить дополнительное преобразование, связывающее точки из мировой системы координат с системой координат камеры.

Это преобразование описывается: - Матрицей вращения $R$ - Вектором переноса $T$

Таким образом, для точки $P_w$ в мировой системе координат её координаты в системе камеры можно вычислить следующим образом:

$P = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix} P_w$ (9)

где: - $R$ — матрица вращения размером 3×3
- $T$ — вектор переноса размером 3×1
- $P_w$ — координаты точки в мировой системе
- $P$ — координаты точки в системе камеры

Подставляя это в уравнение (7) и упрощая, получаем:

$P' = K \begin{bmatrix} R & T \end{bmatrix} P_w = MP_w$ (10)

Параметры $R$ и $T$ называются внешними параметрами, поскольку они:
- Находятся вне камеры
- Не зависят от характеристик камеры

Это завершает описание отображения трёхмерной точки $P$ из произвольной мировой системы координат на плоскость изображения.

Резюме

Полная матрица проекции $M$ состоит из двух типов параметров: - Внутренние параметры (intrinsic parameters) — содержатся в матрице камеры $K$, меняются при смене типа камеры
- Внешние параметры (extrinsic parameters) — включают вращение и перенос, не зависят от конструкции камеры

Полная матрица проекции $M$ размером 3×4 имеет 11 степеней свободы:
- 5 степеней свободы от внутренней матрицы камеры
- 3 степени свободы от внешнего вращения
- 3 степени свободы от внешнего переноса

Таким образом, мы получили полное описание процесса проецирования точки из трёхмерного пространства на плоскость изображения, учитывающее как характеристики самой камеры, так и её положение в пространстве относительно наблюдаемой сцены.

Настройка программного обеспечения

Для работы с нейросетями можно работать через Google Colaboratory. Однако, если у вас уже есть хорошая видеокарта (Nvidia) и вы предпочитаете работать локально, здесь вы найдет инструкции по настройке виртуальной среды.
- Удаленная работа в Google Colaboratory
- Работа локально на вашем компьютере
- Виртуальная среда Anaconda
- Python venv
- Установка пакетов

Удаленная работа в Google Colaboratory

Google Colaboratory — это, по сути, комбинация Jupyter notebook и Google Drive. Он полностью работает в облаке и поставляется с множеством предустановленных заранее пакетами (например, PyTorch и Tensorflow), поэтому у всех есть доступ к одному и тому же широкому перечню библиотек. Кроме того, Google Colab дает бесплатный доступ к аппаратным ускорителям например, K80, P100 и TPU (Tensor Processing Unit).

Требования. Чтобы использовать Colab, у вас должен быть аккаунт Google со связанным Google диском. Предполагается, что у вас есть и то, и другое, вы можете подключить Colab к G-drive, выполнив следующие действия:

1. Нажмите на колесико в правом верхнем углу и выберите Settings.
2. Нажмите на вкладку Manage Apps.
3. Вверху выберите Connect more apps, что должно вызвать окно GSuite Marketplace.
4. Найдите Colab и нажмите Add.

Рекомендации. Есть несколько вещей, о которых вы должны знать при работе с Colab:

1. Постоянное наличие ресурсов не гарантировано (это плата за бесплатность).

2. Если вы бездействуете в течение определенного времени или общее время подключения превышает максимально допустимое время (~12 часов), виртуальная машина Colab будет отключена. Это означает, что любой несохраненный прогресс будет потерян.

Таким образом, выработайте привычку часто сохранять свой код и веса моделей во время работы!

Чтобы узнать больше об ограничениях ресурсов в Colab, ознакомьтесь с их часто задаваемыми вопросами здесь.

Использование графического процессора (GPU). Использовать графический процессор очень просто, нужно просто переключить среду выполнения в Colab. Перейдите в настройки по следующему пути: Runtime -> Change runtime type -> Hardware Accelerator -> GPU , и Colab будет автоматически подкреплен вычислительными мощностями графического процессора.

Если вы хотите узнать больше о Colab, рекомендую вам посетить следующие ресурсы: - Введение в Google Colab - Добро пожаловать в Colab - Обзор функций Colab

Работа на локальном компьютере

Если вы хотите работать локально, вам следует использовать виртуальную среду venv. Вы можете установить ее через Anaconda или через модуль python -m venv.

Виртуальная среда Anaconda

Бесплатный дистрибутив Anaconda Python предоставляет собой набор пакетов для научных вычислений. Приятная вещь в Anaconda заключается в том, что она поставляется с оптимизацией MKL по умолчанию, Это означает, что ваши библиотеки numpy и scipy код получают значительное ускорение без необходимости изменять ни одной строки кода.

После установки Anaconda имеет смысл создать виртуальную среду для отдельного проекта. Если вы не не будете использовать виртуальную среду (настоятельно не рекомендуется!), все зависимости будут установлены глобально на вашем компьютере. Чтобы настроить виртуальную среду с именем mldl, выполните следующие действия в терминале:

conda create -n mldl python=3.12

Чтобы активировать и войти в среду, запустите

conda activate mldl

Чтобы отключить среду, закройте терминал или используйте команду

conda deactivate

Вы можете обратиться к этой странице за более подробными инструкциями по управлению виртуальными средами с помощью Anaconda.

Python venv

Начиная с версии 3.3, Python поставляется с облегченным модулем виртуальной среды под названием venv. Каждая виртуальная среда упаковывает свой собственный независимый набор установленных пакетов (библиотек) Python. Это позволяет изолировать проект от общесистемных пакетов Python и запускать нужную версию Python. Чтобы настроить виртуальную среду с именем mldl, выполните команду в терминале:

python3.12 -m venv mldl

Чтобы активировать и войти в среду, запустите source mldl/bin/activate. Чтобы отключить среду, запустите в терминале deactivate или выйдите из него. Обратите внимание, что каждый раз, когда вы хотите поработать над проектом, вы должны повторно активировать среду.

Установка пакетов

После того как вы настроили и активировали свою виртуальную среду (с помощью conda или venv), вы должны установить библиотеки, необходимые для выполнения назначений с помощью pip. Для этого выполните команду:

pip install -r requirements.txt  

Python IDE

Использование Ide для работы над проектами очень упрощает создание и настройку python. Кроме того, интеграция с Git и другие полезные утилиты позволяют повысить эффективность разработки, не отвлекаясь на рутинные операции. Используйте PyCharm, VsCode или любую другую IDE на ваш вкус. Мой выбор - VsCode с расширениями (Extentions): Python (Microsoft), Black Formatter, JetBrains IDE KeyMapping.

Python numpy (с Jupyter и Colab)

Блокнот Colab

Этот урок был первоначально предоставлен Джастином Джонсоном.

Мы будем использовать язык программирования python для всех заданий этого курса. Python сам по себе является отличным языком программирования общего назначения, но с помощью нескольких популярных библиотек (numpy, scipy, matplotlib) он становится мощной средой для научных вычислений.

Мы ожидаем, что многие из вас имеют некоторый опыт работы с python и numpy. Если нет, то этот раздел послужит кратким ускоренным курсом по обоим направлениям языка программирования python и его использованию для научных исследований и вычислений. Мы также познакомимся с Jupyter-notebooks, которые являются очень удобным способом работы с кодом на python.

Ссылки на полезные ресурсы: - Stepic курс по python - NumPy для пользователей Matlab, - python для пользователей R , - python для пользователей SAS.

Содержание - Блокноты Jupyter и Colab
- Питон
- Версии python
- Основные типы данных
- Контейнеры
- Списках
- Словари
- Множество
- Кортежи
- Функции
- Классы
- Numpy
- Массивы
- Индексация массивов
- Типы данных
- Математические операции с массивами
- Broadcasting
- Документация Numpy
- SciPy
- Операции с изображениями
- Файлы MATLAB
- Расстояние между точками
- Matplotlib
- Постоение кривой
- Побочные сюжеты
- Изображения

Блокноты Jupyter и Colab

Прежде чем мы углубимся в python, мы хотели бы кратко поговорить о блокнотах. Блокнот Jupyter позволяет писать и выполнять код python локально в вашем веб-браузере. Jupyter notebooks yпрощает работу с кодом и выполняет его по блокам. По этой причине он широко используется в научных вычислениях. Colab, с другой стороны, является разновидностью Google-блокнота Jupyter, который особенно подходит для машинных алгоритмов обучения и анализа данных, которые сохраняют функционал в облаке. Colab — это, по сути, Jupyter notebook на стероидах: он бесплатный, не требует настройки, поставляется с предустановленными пакетами, им легко поделиться со всем миром. В нем присутствуют преимущества бесплатного доступа к аппаратным ускорителям, таким как графические процессоры и TPU (с некоторыми оговорками).

Запустите Tutorial в Colab (рекомендуется). Если вы хотите выполнить это руководство полностью в Colab, нажмите на значок Open in Colab в самом верху этой страницы.

Запустите Tutorial в блокноте Jupyter. Если вы хотите запустить блокнот локально с помощью Jupyter, убедитесь, что ваша виртуальная среда установлена правильно (в соответствии с инструкциями по настройке), активируйте ее, а затем запустите pip install notebook для установки блокнота Jupyter. Затем откройте блокнот и загрузите его в каталог по вашему выбору, щелкнув правой кнопкой мыши по странице и выбрав Save Page As. Затем cd в этот каталог и запустите jupyter notebook.

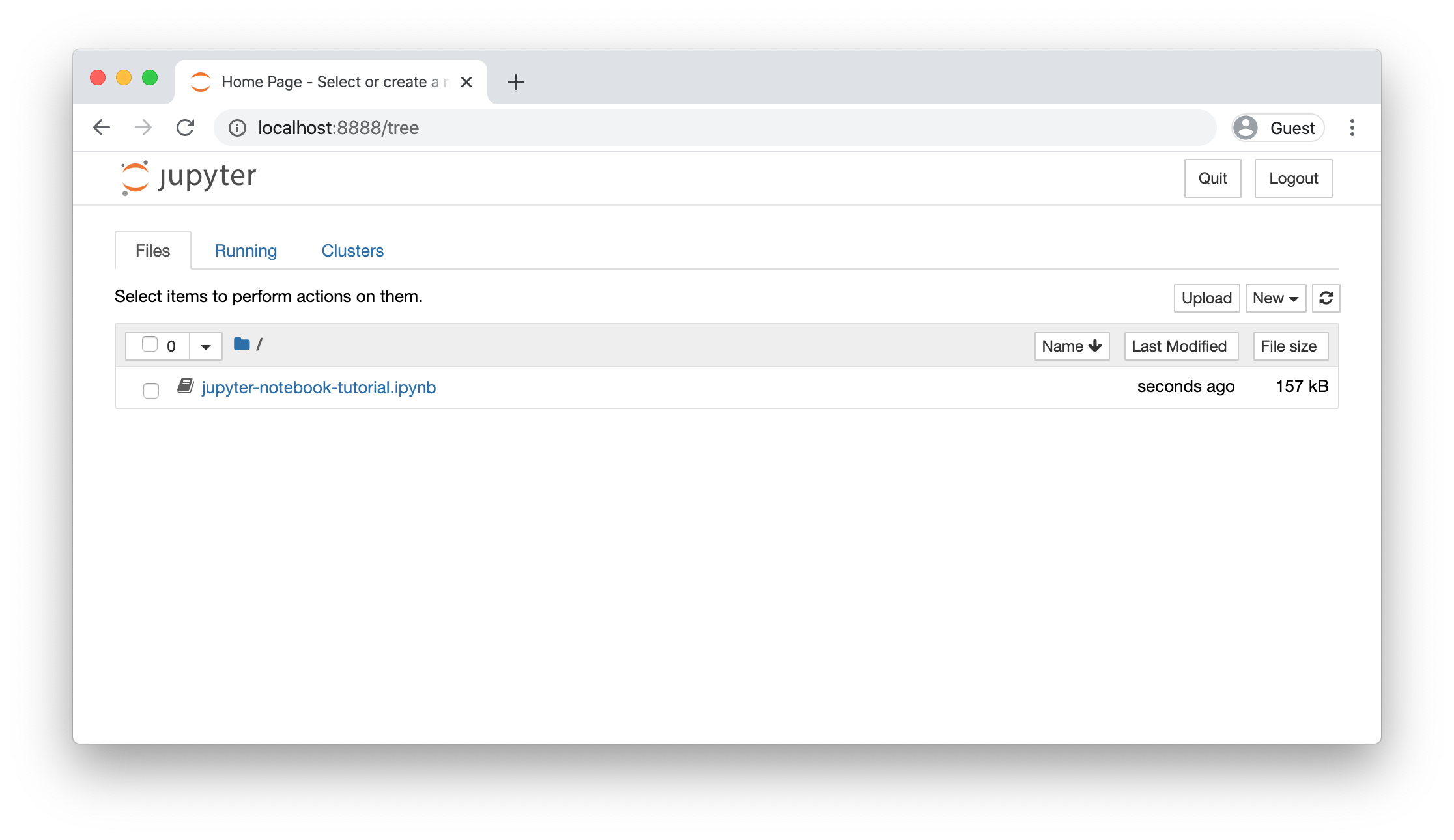
Это должно автоматически запустить сервер блокнотов по адресу http://localhost:8888. Если все работало правильно, вы должны увидеть такой экран, показывающий все доступные записные книжки в текущем каталоге. Нажмите jupyter-notebook-tutorial.ipynb и следуйте инструкциям в блокноте. В противном случае вы можете продолжить чтение туториала с фрагментами кода ниже.

Python

Python — это высокоуровневый, динамически типизированный мультипарадигмальный язык программирования. О коде на python часто говорят, что он похож на псевдокод, поскольку он позволяет вам выражать очень мощные идеи в очень немногих строках кода, оставаясь при этом очень удобочитаемый. В качестве примера приведем реализацию алгоритма классической быстрой сортировки на python:

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

print(quicksort([3,6,8,10,1,2,1]))
# Prints "[1, 1, 2, 3, 6, 8, 10]"

Версии python

С 1 января 2020 года python официально прекратил поддержку второй версии. Поэтому во всех примерах код написан на python 3.7. Убедитесь, что вы правильно установили виртуальную среду, прежде чем продолжить работу с этим руководством. Вы можете проверить свою версию в командной строке после активации среды, запустив команду: python --version

Основные типы данных

Как и большинство языков, python имеет ряд основных типов: int, floats, booleans и strings. Эти типы данных ведут себя так же, как и в большинстве других языков программирования.

Числа:

x = 3
print(type(x)) # Prints "<class 'int'>"
print(x)       # Prints "3"
print(x + 1)   # Addition; prints "4"
print(x - 1)   # Subtraction; prints "2"
print(x * 2)   # Multiplication; prints "6"
print(x ** 2)  # Exponentiation; prints "9"
x += 1
print(x)  # Prints "4"
x *= 2
print(x)  # Prints "8"
y = 2.5
print(type(y)) # Prints "<class 'float'>"
print(y, y + 1, y * 2, y ** 2) # Prints "2.5 3.5 5.0 6.25"

Обратите внимание, что в отличие от многих языков, в python нет унарного инкремента (x++) или декремента (x--).

Python также имеет встроенные типы для комплексных чисел; Все подробности можно найти в документации.

Логический тип данных: python реализует все обычные операторы для булевой логики, но использует английские слова, а не символы (&&, || , и т. д.):

t = True
f = False
print(type(t)) # Prints "<class 'bool'>"
print(t and f) # Logical AND; prints "False"
print(t or f)  # Logical OR; prints "True"
print(not t)   # Logical NOT; prints "False"
print(t != f)  # Logical XOR; prints "True"

Строки: python имеет отличную поддержку строк:

hello = 'hello'    # String literals can use single quotes
world = "world"    # or double quotes; it does not matter.
print(hello)       # Prints "hello"
print(len(hello))  # String length; prints "5"
hw = hello + ' ' + world  # String concatenation
print(hw)  # prints "hello world"
hw12 = '%s %s %d' % (hello, world, 12)  # sprintf style string formatting
print(hw12)  # prints "hello world 12"  

Строковые объекты имеют множество полезных методов:

s = "hello"
print(s.capitalize())  # Capitalize a string; prints "Hello"
print(s.upper())       # Convert a string to uppercase; prints "HELLO"
print(s.rjust(7))      # Right-justify a string, padding with spaces; prints "  hello"
print(s.center(7))     # Center a string, padding with spaces; prints " hello "
print(s.replace('l', '(ell)'))  # Replace all instances of one substring with another;
                                # prints "he(ell)(ell)o"
print('  world '.strip())  # Strip leading and trailing whitespace; prints "world"

Список всех строковых методов можно найти в документации.

Контейнеры

Python включает в себя несколько встроенных типов контейнеров: списки, словари, наборы и кортежи.

Списки

Список в python является эквивалентом массива, но его размер можно изменять и он можетё содержать элементы разных типов:

xs = [3, 1, 2]    # Create a list
print(xs, xs[2])  # Prints "[3, 1, 2] 2"
print(xs[-1])     # Negative indices count from the end of the list; prints "2"
xs[2] = 'foo'     # Lists can contain elements of different types
print(xs)         # Prints "[3, 1, 'foo']"
xs.append('bar')  # Add a new element to the end of the list
print(xs)         # Prints "[3, 1, 'foo', 'bar']"
x = xs.pop()      # Remove and return the last element of the list
print(x, xs)      # Prints "bar [3, 1, 'foo']"  

Как обычно, вы можете найти подробности о списках в документации.

Разрезание на ломтики: В дополнение к доступу к элементам списка по одному, python предоставляет лаконичный синтаксис для доступа к подспискам; Это называется нарезкой:

nums = list(range(5))     # range is a built-in function that creates a list of integers
print(nums)               # Prints "[0, 1, 2, 3, 4]"
print(nums[2:4])          # Get a slice from index 2 to 4 (exclusive); prints "[2, 3]"
print(nums[2:])           # Get a slice from index 2 to the end; prints "[2, 3, 4]"
print(nums[:2])           # Get a slice from the start to index 2 (exclusive); prints "[0, 1]"
print(nums[:])            # Get a slice of the whole list; prints "[0, 1, 2, 3, 4]"
print(nums[:-1])          # Slice indices can be negative; prints "[0, 1, 2, 3]"
nums[2:4] = [8, 9]        # Assign a new sublist to a slice
print(nums)               # Prints "[0, 1, 8, 9, 4]" 

Мы снова увидим нарезку в контексте массивов numpy.

Петли: Вы можете перебирать элементы списка следующим образом:

animals = ['cat', 'dog', 'monkey']
for animal in animals:
    print(animal)
# Prints "cat", "dog", "monkey", each on its own line.

Если вы хотите получить доступ к индексу каждого элемента в теле цикла, воспользуйтесь встроенной функцией:enumerate

animals = ['cat', 'dog', 'monkey']
for idx, animal in enumerate(animals):
    print('#%d: %s' % (idx + 1, animal))
# Prints "#1: cat", "#2: dog", "#3: monkey", each on its own line  

Список включений: при программировании мы часто хотим преобразовать один тип данных в другой. В качестве простого примера рассмотрим следующий код, который вычисляет квадратные числа:

nums = [0, 1, 2, 3, 4]
squares = []
for x in nums:
    squares.append(x ** 2)
print(squares)   # Prints [0, 1, 4, 9, 16]

Вы можете упростить этот код с помощью спискового понимания:

nums = [0, 1, 2, 3, 4]
squares = [x ** 2 for x in nums]
print(squares)   # Prints [0, 1, 4, 9, 16]

Включения списка также могут содержать условия:

nums = [0, 1, 2, 3, 4]
even_squares = [x ** 2 for x in nums if x % 2 == 0]
print(even_squares)  # Prints "[0, 4, 16]"

Словари

Словарь хранит пары (ключ, значение), аналогично Map в Java или объекту в Javascript. Вы можете использовать его следующим образом:

d = {'cat': 'cute', 'dog': 'furry'}  # Create a new dictionary with some data
print(d['cat'])       # Get an entry from a dictionary; prints "cute"
print('cat' in d)     # Check if a dictionary has a given key; prints "True"
d['fish'] = 'wet'     # Set an entry in a dictionary
print(d['fish'])      # Prints "wet"
# print(d['monkey'])  # KeyError: 'monkey' not a key of d
print(d.get('monkey', 'N/A'))  # Get an element with a default; prints "N/A"
print(d.get('fish', 'N/A'))    # Get an element with a default; prints "wet"
del d['fish']         # Remove an element from a dictionary
print(d.get('fish', 'N/A')) # "fish" is no longer a key; prints "N/A"

Все, что вам нужно знать о словарях, вы можете найти в документации.

Петли: Перебирать ключи в словаре очень просто:

d = {'person': 2, 'cat': 4, 'spider': 8}
for animal in d:
    legs = d[animal]
    print('A %s has %d legs' % (animal, legs))
# Prints "A person has 2 legs", "A cat has 4 legs", "A spider has 8 legs" 

Если вы хотите получить доступ к ключам и их соответствующим значениям, используйте метод:items

d = {'person': 2, 'cat': 4, 'spider': 8}
for animal, legs in d.items():
    print('A %s has %d legs' % (animal, legs))
# Prints "A person has 2 legs", "A cat has 4 legs", "A spider has 8 legs"

Словарное понимание: Они похожи на включения списков, но позволяют легко создавать cловари. Например:

nums = [0, 1, 2, 3, 4]
even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0}
print(even_num_to_square)  # Prints "{0: 0, 2: 4, 4: 16}"

Наборы

Наборы — это неупорядоченное множество отдельных элементов. В качестве простого примера рассмотрим следующее:

animals = {'cat', 'dog'}
print('cat' in animals)   # Check if an element is in a set; prints "True"
print('fish' in animals)  # prints "False"
animals.add('fish')       # Add an element to a set
print('fish' in animals)  # Prints "True"
print(len(animals))       # Number of elements in a set; prints "3"
animals.add('cat')        # Adding an element that is already in the set does nothing
print(len(animals))       # Prints "3"
animals.remove('cat')     # Remove an element from a set
print(len(animals))       # Prints "2"

Как обычно, все, что вы хотите знать о множествах, можно найти в документации.

Петли: Перебор набора имеет тот же синтаксис, что и перебор списка; Однако, поскольку наборы не упорядочены, вы не можете делать предположения о порядке, в которых вы посещаете элементы набора:

animals = {'cat', 'dog', 'fish'}
for idx, animal in enumerate(animals):
    print('#%d: %s' % (idx + 1, animal))
# Prints "#1: fish", "#2: dog", "#3: cat"  

Набор понятий: подобно спискам и словарям, мы можем легко создавать наборы, используя включения множеств:

from math import sqrt
nums = {int(sqrt(x)) for x in range(30)}
print(nums)  # Prints "{0, 1, 2, 3, 4, 5}"

Кортежи

Кортеж — это (неизменяемый) упорядоченный список значений. Кортеж во многом похож на список; Одним из наиболее важных отличий является то, что кортежи можно использовать как ключи в словарях и как элементы множеств, а списки — нет. Вот банальный пример:

d = {(x, x + 1): x for x in range(10)}  # Create a dictionary with tuple keys
t = (5, 6)        # Create a tuple
print(type(t))    # Prints "<class 'tuple'>"
print(d[t])       # Prints "5"
print(d[(1, 2)])  # Prints "1"

В документации есть больше информации о кортежах.

Функции

Функции python определяются с помощью ключевого слова. Например:def

def sign(x):
    if x > 0:
        return 'positive'
    elif x < 0:
        return 'negative'
    else:
        return 'zero'

for x in [-1, 0, 1]:
    print(sign(x))
# Prints "negative", "zero", "positive"

Мы часто определяем функции, принимающие необязательные аргументы ключевых слов, например:

def hello(name, loud=False):
    if loud:
        print('HELLO, %s!' % name.upper())
    else:
        print('Hello, %s' % name)

hello('Bob') # Prints "Hello, Bob"
hello('Fred', loud=True)  # Prints "HELLO, FRED!" 

В документации есть гораздо больше информации о функциях python.

Классы

Синтаксис для определения классов в python прост:

class Greeter(object):

    # Constructor
    def **init**(self, name):
        self.name = name  # Create an instance variable

    # Instance method
    def greet(self, loud=False):
        if loud:
            print('HELLO, %s!' % self.name.upper())
        else:
            print('Hello, %s' % self.name)

g = Greeter('Fred')  # Construct an instance of the Greeter class
g.greet()            # Call an instance method; prints "Hello, Fred"
g.greet(loud=True)   # Call an instance method; prints "HELLO, FRED!"

Вы можете прочитать гораздо больше о классах python в документации.

Numpy

Numpy — это основная библиотека для научных вычислений на языке python. Она предоставляет высокопроизводительный многомерный массив объектов и инструменты для работы с ними Массивы. Если вы уже знакомы с MATLAB, то этот урок может быть вам полезен для начала работы с Numpy.

Массивы

Массив numpy представляет собой сетку значений одного и того же типа, индексирующую кортежем неотрицательные целые числа. Количество измерений — это ранг массива; Форма массива представляет собой кортеж целых чисел, задающий размер массива вдоль каждого измерения.

Мы можем инициализировать массивы numpy из вложенных списков python, и получить доступ к элементам с помощью квадратных скобок:

 import numpy as np

a = np.array([1, 2, 3])   # Create a rank 1 array
print(type(a))            # Prints "<class 'numpy.ndarray'>"
print(a.shape)            # Prints "(3,)"
print(a[0], a[1], a[2])   # Prints "1 2 3"
a[0] = 5                  # Change an element of the array
print(a)                  # Prints "[5, 2, 3]"

b = np.array([[1,2,3],[4,5,6]])    # Create a rank 2 array
print(b.shape)                     # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0])   # Prints "1 2 4"  

Numpy также предоставляет множество функций для создания массивов:

import numpy as np

a = np.zeros((2,2))   # Create an array of all zeros
print(a)              # Prints "[[ 0.  0.]
                      #          [ 0.  0.]]"

b = np.ones((1,2))    # Create an array of all ones
print(b)              # Prints "[[ 1.  1.]]"

c = np.full((2,2), 7)  # Create a constant array
print(c)               # Prints "[[ 7.  7.]
                       #          [ 7.  7.]]"

d = np.eye(2)         # Create a 2x2 identity matrix
print(d)              # Prints "[[ 1.  0.]
                      #          [ 0.  1.]]"

e = np.random.random((2,2))  # Create an array filled with random values
print(e)                     # Might print "[[ 0.91940167  0.08143941]
                             #               [ 0.68744134  0.87236687]]"

О других способах создания массивов вы можете прочитать в документации.

Индексация массивов

Numpy предлагает несколько способов индексации в массивы.

Разрезание на ломтики: как и в случае со списками python, массивы numpy могут быть разделены на срезы. Поскольку массивы могут быть многомерными, необходимо указать срез для каждого измерения массива:

import numpy as np

# Create the following rank 2 array with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])

# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
#  [6 7]]
b = a[:2, 1:3]

# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1])   # Prints "2"
b[0, 0] = 77     # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1])   # Prints "77"

Вы также можете сочетать целочисленное индексирование с индексированием срезов. Однако это приведет к получению массива более низкого ранга, чем исходный массив. Обратите внимание, что это сильно отличается от способа, которым MATLAB работает с массивами при разрезании на ломтики:

import numpy as np

# Create the following rank 2 array with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])

# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :]    # Rank 1 view of the second row of a
row_r2 = a[1:2, :]  # Rank 2 view of the second row of a
print(row_r1, row_r1.shape)  # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape)  # Prints "[[5 6 7 8]] (1, 4)"

# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)  # Prints "[ 2  6 10] (3,)"
print(col_r2, col_r2.shape)  # Prints "[[ 2]
                             #          [ 6]
                             #          [10]] (3, 1)"

Индексация целочисленного массива: Когда вы индексируете массивы numpy с помощью слайсинга, результирующее представление массива всегда будет подмассивом исходного массива. В противоположность этому, индексация целочисленного массива позволяет создавать произвольные массивы, используя данные из другого массива. Вот пример:

import numpy as np

a = np.array([[1,2], [3, 4], [5, 6]])

# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]])  # Prints "[1 4 5]"

# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))  # Prints "[1 4 5]"

# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]])  # Prints "[2 2]"

# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]]))  # Prints "[2 2]"

Одним из полезных приемов при индексации целочисленных массивов является выбор или изменение в одногм из них каждой строки матрицы:

import numpy as np

# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])

print(a)  # prints "array([[ 1,  2,  3],
          #                [ 4,  5,  6],
          #                [ 7,  8,  9],
          #                [10, 11, 12]])"

# Create an array of indices
b = np.array([0, 2, 0, 1])

# Select one element from each row of a using the indices in b
print(a[np.arange(4), b])  # Prints "[ 1  6  7 11]"

# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10

print(a)  # prints "array([[11,  2,  3],
          #                [ 4,  5, 16],
          #                [17,  8,  9],
          #                [10, 21, 12]])

Индексация логических массивов: Логическое индексирование массива позволяет выделять произвольные элементы массива. Часто этот тип индексации используется для выбора элементов массива которые удовлетворяют какому-либо условию. Вот пример:

import numpy as np

a = np.array([[1,2], [3, 4], [5, 6]])

bool_idx = (a > 2)   # Find the elements of a that are bigger than 2;
                     # this returns a numpy array of Booleans of the same
                     # shape as a, where each slot of bool_idx tells
                     # whether that element of a is > 2.

print(bool_idx)      # Prints "[[False False]
                     #          [ True  True]
                     #          [ True  True]]"

# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx])  # Prints "[3 4 5 6]"

# We can do all of the above in a single concise statement:
print(a[a > 2])     # Prints "[3 4 5 6]"

Для краткости мы опустили много подробностей об индексации массива numpy; Если вы хотите узнать больше, вам следует прочитать документацию.

Типы данных

Каждый массив numpy представляет собой сетку элементов одного типа. Numpy предоставляет большой набор числовых типов данных, которые можно использовать для создания массивов. Numpy пытается определить тип данных при создании массива, но функции, создающие массивы, обычно также включают необязательный аргумент для явного указания типа данных. Вот пример:

import numpy as np

x = np.array([1, 2])   # Let numpy choose the datatype
print(x.dtype)         # Prints "int64"

x = np.array([1.0, 2.0])   # Let numpy choose the datatype
print(x.dtype)             # Prints "float64"

x = np.array([1, 2], dtype=np.int64)   # Force a particular datatype
print(x.dtype)                         # Prints "int64"

Вы можете прочитать все о типах данных numpy в документации.

Математические операции с массивами

Основные математические функции работают с массивами поэлементно и доступны как в виде перегрузок операторов, так и в виде функций в модуле numpy:

import numpy as np

x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)

# Elementwise sum; both produce the array
# [[ 6.0  8.0]
#  [10.0 12.0]]
print(x + y)
print(np.add(x, y))

# Elementwise difference; both produce the array
# [[-4.0 -4.0]
#  [-4.0 -4.0]]
print(x - y)
print(np.subtract(x, y))

# Elementwise product; both produce the array
# [[ 5.0 12.0]
#  [21.0 32.0]]
print(x * y)
print(np.multiply(x, y))

# Elementwise division; both produce the array
# [[ 0.2         0.33333333]
#  [ 0.42857143  0.5       ]]
print(x / y)
print(np.divide(x, y))

# Elementwise square root; produces the array
# [[ 1.          1.41421356]
#  [ 1.73205081  2.        ]]
print(np.sqrt(x))

Обратите внимание, что в отличие от MATLAB,*- это поэлементное умножение, а не матрица умножение. Вместо этого мы используем функцию dot для вычисления скалярного произведения векторов, умножить вектор на матрицу, и умножения матриц. dot доступен как функция в numpy и в качестве экземпляра метода объектов массива:

import numpy as np

x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])

v = np.array([9,10])
w = np.array([11, 12])

# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))

# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))

# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
#  [43 50]]
print(x.dot(y))
print(np.dot(x, y))

Numpy предоставляет множество полезных функций для выполнения вычислений на массивах; Одной из самых полезных является:sum

import numpy as np

x = np.array([[1,2],[3,4]])

print(np.sum(x))  # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0))  # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1))  # Compute sum of each row; prints "[3 7]"

Полный список математических функций, предоставляемых numpy, вы можете найти в документации.

Помимо вычисления математических функций с помощью массивов, мы часто должны изменять форму данных в массивах или иным образом манипулировать ими. Самый простой пример. Одним из таких видов операции является транспонирование матрицы; для транспонирования матрицы, просто используйте атрибут T объекта массива:

import numpy as np

x = np.array([[1,2], [3,4]])
print(x)    # Prints "[[1 2]
            #          [3 4]]"
print(x.T)  # Prints "[[1 3]
            #          [2 4]]"

# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v)    # Prints "[1 2 3]"
print(v.T)  # Prints "[1 2 3]"

Numpy предоставляет гораздо больше функций для работы с массивами; С полным списком можно ознакомиться в документации.

Вещание

Вещание - это мощный механизм, который позволяет numpy работать с массивами различных фигур при выполнении арифметических действий. Часто у нас есть меньший массив и больший массив, и мы хотим использовать меньший массив несколько раз для выполнения какой-либо операции на более крупном массиве.

Например, предположим, что мы хотим добавить вектор константы к каждой строке матрицы. Мы могли бы сделать это следующим образом:

import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x)   # Create an empty matrix with the same shape as x

# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
    y[i, :] = x[i, :] + v

# Now y is the following
# [[ 2  2  4]
#  [ 5  5  7]
#  [ 8  8 10]
#  [11 11 13]]
print(y) 

Это работает, однако, когда матрица x очень большая, вычисление явного цикла в python может быть медленным. Обратите внимание, что добавление вектора v к каждой строке матрицы x эквивалентно формированию матрицы vv путем наложения нескольких копий v по вертикали, затем выполнение поэлементного суммирования x и vv мы могли бы реализовать этот подход следующим образом:

import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
vv = np.tile(v, (4, 1))   # Stack 4 copies of v on top of each other
print(vv)                 # Prints "[[1 0 1]
                          #          [1 0 1]
                          #          [1 0 1]
                          #          [1 0 1]]"
y = x + vv  # Add x and vv elementwise
print(y)  # Prints "[[ 2  2  4
          #          [ 5  5  7]
          #          [ 8  8 10]
          #          [11 11 13]]"

Массивы Numpy позволяют выполнять вычисления без фактического создания нескольких копий v. Рассмотрим эту версию с использованием массивов:

import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v  # Add v to each row of x using broadcasting
print(y)  # Prints "[[ 2  2  4]
          #          [ 5  5  7]
          #          [ 8  8 10]
          #          [11 11 13]]"

Строка y = x + v работает, несмотря на то, что x имеет форму (4, 3)и v имеет форму (3,) благодаря вещанию; Эта линия работает так, как будто v на самом деле имеет форму (4, 3), где каждая строка была копией , а сумма v выполнялась по элементам.

Трансляция двух массивов одновременно выполняется по следующим правилам: 1. Если массивы имеют разный ранг, добавьте в начало форму массива с меньшим рангом с 1s до тех пор, пока обе фигуры не будут иметь одинаковую длину. 2. Два массива считаются совместимыми в размерности, если они имеют одинаковое значение size в измерении, или если один из массивов имеет размер 1 в этом измерении. 3. Массивы могут транслироваться вместе, если они совместимы во всех измерениях. 4. После трансляции каждый массив ведет себя так, как если бы он имел форму, равную поэлементной максимальное количество форм двух входных массивов. 5. В любом измерении, где один массив имеет размер 1, а другой массив больше 1, первый массив ведет себя так, как если бы он был скопирован по этому размеру

Если это объяснение не имеет смысла, попробуйте прочитать объяснение из документации или это объяснение.

Функции, поддерживающие широковещательную рассылку, называются универсальными функциями. Вы можете найти Список всех универсальных функций в документации.

Вот некоторые области применения вещания:

import numpy as np

# Compute outer product of vectors
v = np.array([1,2,3])  # v has shape (3,)
w = np.array([4,5])    # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4  5]
#  [ 8 10]
#  [12 15]]
print(np.reshape(v, (3, 1)) * w)

# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
#  [5 7 9]]
print(x + v)

# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5  6  7]
#  [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))

# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2  4  6]
#  [ 8 10 12]]
print(x * 2)  

Широковещательная рассылка обычно делает ваш код более кратким и быстрым, поэтому вы должен стремиться использовать ее там, где это возможно.

Документация Numpy

Этот краткий обзор затронул многие важные вещи, которые вам необходимо знать о numpy, но далеко не полны. Ознакомьтесь со справочником numpy, чтобы узнать больше о numpy.

SciPy

Numpy предоставляет высокопроизводительный многомерный массив и основные инструменты для выполняйте вычисления с помощью этих массивов и управляйте ими. SciPy опирается на это и предоставляет большое количество функций, которые работают с массивами numpy и полезны для различных видов научных и инженерных приложений.

Лучший способ познакомиться с SciPy - это просмотреть документацию. Мы выделим некоторые части SciPy, которые могут быть вам полезны для этого класса.

Операции с изображениями

SciPy предоставляет некоторые основные функции для работы с изображениями. Например, в нем есть функции чтения изображений с диска в массивы numpy, для записи массивов numpy на диск в виде изображений, а также для изменения размера изображений. Вот простой пример, демонстрирующий эти функции:

from scipy.misc import imread, imsave, imresize

# Read an JPEG image into a numpy array
img = imread('assets/cat.jpg')
print(img.dtype, img.shape)  # Prints "uint8 (400, 248, 3)"

# We can tint the image by scaling each of the color channels
# by a different scalar constant. The image has shape (400, 248, 3);
# we multiply it by the array [1, 0.95, 0.9] of shape (3,);
# numpy broadcasting means that this leaves the red channel unchanged,
# and multiplies the green and blue channels by 0.95 and 0.9
# respectively.
img_tinted = img * [1, 0.95, 0.9]

# Resize the tinted image to be 300 by 300 pixels.
img_tinted = imresize(img_tinted, (300, 300))

# Write the tinted image back to disk
imsave('assets/cat_tinted.jpg', img_tinted)

Сверху: исходное изображение. Снизу: Затемненное изображение с измененным размером.

Файлы MATLAB

Функции scipy.io.loadmat и scipy.io.savemat позволяют считывать и писать файлы MATLAB. О них можно прочитать в документации.

Расстояние между точками

SciPy определяет некоторые полезные функции для вычисления расстояний между наборами точек.

Функция scipy.spatial.distance.pdist вычисляет расстояние между всеми парами точек в заданном наборе:

import numpy as np
from scipy.spatial.distance import pdist, squareform

# Create the following array where each row is a point in 2D space:
# [[0 1]
#  [1 0]
#  [2 0]]
x = np.array([[0, 1], [1, 0], [2, 0]])
print(x)

# Compute the Euclidean distance between all rows of x.
# d[i, j] is the Euclidean distance between x[i, :] and x[j, :],
# and d is the following array:
# [[ 0.          1.41421356  2.23606798]
#  [ 1.41421356  0.          1.        ]
#  [ 2.23606798  1.          0.        ]]
d = squareform(pdist(x, 'euclidean'))
print(d)

Все подробности об этой функции вы можете прочитать в документации.

Аналогичная функция (scipy.spatial.distance.cdist) вычисляет расстояние между всеми парами по двум группам точек; Вы можете прочитать об этом в документации .

Matplotlib

Matplotlib — библиотека для построения графиков. В этом разделе дается краткое введение в модуль matplotlib.pyplot, который обеспечивает систему построения графиков, аналогичную системе MATLAB.

Постоение графиков

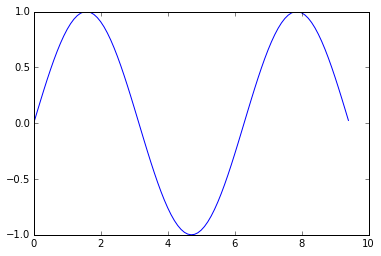
Наиболее важной функцией в matplotlib является plot, что позволяет строить графики 2D данных. Вот простой пример:

import numpy as np
import matplotlib.pyplot as plt

# Compute the x and y coordinates for points on a sine curve
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)

# Plot the points using matplotlib
plt.plot(x, y)
plt.show()  # You must call plt.show() to make graphics appear.

Выполнение этого кода создает следующий график:

Приложив немного дополнительной работы, мы можем легко построить несколько линий и добавить заголовок, легенду и подписи осям:

import numpy as np
import matplotlib.pyplot as plt

# Compute the x and y coordinates for points on sine and cosine curves
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)

# Plot the points using matplotlib
plt.plot(x, y_sin)
plt.plot(x, y_cos)
plt.xlabel('x axis label')
plt.ylabel('y axis label')
plt.title('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])
plt.show()

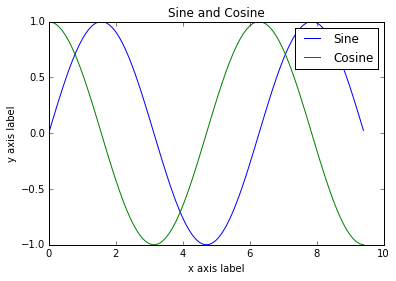
Гораздо больше о функции plot вы можете прочитать в документации.

Подзаголовки

С помощью subplot функции на одном и том же рисунке можно изобразить разные объекты. Вот пример:

import numpy as np
import matplotlib.pyplot as plt

# Compute the x and y coordinates for points on sine and cosine curves
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)

# Set up a subplot grid that has height 2 and width 1,
# and set the first such subplot as active.
plt.subplot(2, 1, 1)

# Make the first plot
plt.plot(x, y_sin)
plt.title('Sine')

# Set the second subplot as active, and make the second plot.
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')

# Show the figure.
plt.show()

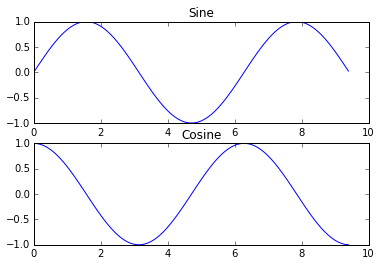
Гораздо больше о функции subplot вы можете прочитать в документации.

Изображения

Вы можете использовать функцию imshow для показа изображений. Вот пример:

import numpy as np
from scipy.misc import imread, imresize
import matplotlib.pyplot as plt

img = imread('assets/cat.jpg')
img_tinted = img * [1, 0.95, 0.9]

# Show the original image
plt.subplot(1, 2, 1)
plt.imshow(img)

# Show the tinted image
plt.subplot(1, 2, 2)

# A slight gotcha with imshow is that it might give strange results
# if presented with data that is not uint8. To work around this, we
# explicitly cast the image to uint8 before displaying it.
plt.imshow(np.uint8(img_tinted))
plt.show()

Классификация изображений

В этой лекции мы познакомимся с проблемой классификации изображений. Решение проблемы заключается в подходе, основанном на большом объеме размеченных данных.

Содержание:
- Введение в классификацию изображений
- Классификатор ближайшего соседа
- Классификатор k - ближайших соседей
- Наборы данных для настройки гиперпараметров
- Применение kNN на практике
- Дополнительные материалы

Введение в классификацию изображений

Мотивация. В этом разделе мы рассмотрим задачу классификации изображений. Задача заключается в присвоении входному изображению одной метки из фиксированного набора категорий. Это одна из основных задач компьютерного зрения, которая, несмотря на свою простоту, имеет множество практических применений. Более того, многие другие задачи компьютерного зрения (детекция объектов, сегментация) могут быть сведены к классификации изображений.

Пример. Например, на изображении ниже модель классификации изображений принимает одно изображение и присваивает вероятности четырём меткам: {«кошка», «собака», «шляпа», «кружка»}. Как показано на изображении, для компьютера изображение представляет собой один большой трёхмерный массив чисел. В этом примере изображение кошки имеет ширину 248 пикселей, высоту 400 пикселей и три цветовых канала: красный, зелёный, синий (или сокращённо RGB). Таким образом, изображение состоит из 248 x 400 x 3 чисел, или в общей сложности 297 600 чисел. Каждое число представляет собой целое число от 0 (чёрный) до 255 (белый). Наша задача — превратить эти четверть миллиона чисел в одну метку, например «кошка».

Задача классификации изображений состоит в том, чтобы предсказать одну метку для заданного изображения. Так же мы можем предсказать распределение вероятностей для всех меток, что отражает степень нашей уверенности в результате классификации. Изображения представляют собой трёхмерные массивы целых чисел от 0 до 255 размером «ширина x высота x 3». Число 3 обозначает три цветовых канала: красный, зелёный и синий.

Проблемы. Поскольку задача распознавания визуального образа (например, кошки) относительно проста для человека, стоит рассмотреть связанные с ней проблемы с точки зрения алгоритма компьютерного зрения.
Ниже мы приводим (неполный) список проблем, не забывая о том, что изображения представлены в виде трёхмерного массива значений яркости:
- Изменение точки обзора. Один экземпляр объекта может быть ориентирован по-разному относительно камеры.
- Изменение масштаба. Визуальные классы часто различаются по размеру (размеру в реальном мире, а не только по размеру на изображении).
- Деформация. Многие интересующие нас объекты не являются твёрдыми телами и могут сильно деформироваться.
- Окклюзия. Интересующие нас объекты могут быть частично скрыты. Иногда видна лишь небольшая часть объекта (всего несколько пикселей).
- Условия освещения. Влияние освещения на пиксели очень велико.
- Фоновый шум. Интересующие нас объекты могут сливаться с окружающей средой, что затрудняет их идентификацию.
- Внутриклассовые различия. Классы, представляющие интерес, часто могут быть относительно обширными, например, стулья. Существует множество различных типов этих предметов, каждый из которых имеет отличный от других элементов класса внешний вид.

Хорошая модель классификации изображений должна быть инвариантна к перекрёстному произведению всех этих вариаций, сохраняя при этом чувствительность к межклассовым вариациям.

Подход, основанный на данных. Как бы мы могли написать алгоритм, который сможет классифицировать изображения по отдельным категориям? В отличие от написания алгоритма, например, для сортировки списка чисел, не очевидно, как можно написать алгоритм для распознавания кошек на изображениях. Поэтому вместо того, чтобы пытаться описать каждую из интересующих нас категорий непосредственно в коде, мы воспользуемся подходом, похожим на обучение ребёнка. Мы предоставим компьютеру множество примеров, а затем используем алгоритм обучения, который связывает визуальное представление с меткой каждого класса. Этот подход предполагает, что у нас есть обучающий набор с размеченными изображениями. Вот пример того, как может выглядеть такой набор данных:

Пример обучающего набора для четырёх визуальных категорий. На практике у нас могут быть тысячи категорий и сотни тысяч изображений для каждой категории.

Конвейер классификации изображений. Мы увидели, что задача классификации изображений состоит в том, чтобы взять массив пикселей изображения и присвоить ему метку. Наш полный конвейер можно формализовать следующим образом:
- Входные данные: состоят из набора N изображений, каждое из которых помечено одним из K различных классов. Эти данные называются обучающей выборкой.
- Обучение: наша задача использовать обучающую выборку, чтобы узнать, как выглядит каждый из классов. Мы называем этот этап обучением классификатора или обучением модели.
- Оценка: в конце мы оцениваем качество классификатора. Для этого нужно задать вопрос о том, какие метки предскажет классификатор для нового набора изображений, которые он никогда раньше не видел. Затем мы сравниваем истинные метки этих изображений с теми, которые предсказал классификатор. Интуитивно мы надеемся, что многие прогнозы совпадут с истинными ответами. Данные, которые используются для оценки точности классификатора называются тестовой выборкой.

Классификатор ближайшего соседа

В качестве первого подхода мы используем так называемый классификатор ближайшего соседа. Этот классификатор не имеет ничего общего со свёрточными нейронными сетями и очень редко используется на практике. Однако он позволит нам получить представление о том, как решается задача классификации изображений.

Пример набора данных для классификации изображений: CIFAR-10.
Одним из популярных наборов данных для классификации изображений является набор данных CIFAR-10. Этот набор данных состоит из 60 000 крошечных изображений высотой и шириной 32 пикселя. Каждое изображение относится к одному из 10 классов: самолет, автомобиль, птица и т. д. Эти 60 000 изображений разделены на обучающую выборку из 50 000 изображений и тестовую выборку из 10 000 изображений. На изображении ниже вы можете увидеть 10 случайных примеров изображений для каждого класса.

Слева: примеры изображений из набора данных CIFAR-10.
Справа: в первом столбце показаны несколько тестовых изображений.
Рядом с каждым изображением мы видим 10 наиболее похожих "картинок" из обучающей выборки.

Изначально, у нас есть обучающая выборка CIFAR-10 из 50 000 изображений (по 5000 изображений для каждой из 10 категорий). Мы хотим классифицировать оставшиеся 10 000. Классификатор ближайших соседей работает следующим образом. Берется тестовое изображение и сравается с каждым изображением из обучающей выборки. Будем считать, что метка тестового изображения будет такой же, как и у самого похожего на него изображения.

На изображении выше и справа вы можете увидеть пример результата такой процедуры для 10 тестовых изображений. Обратите внимание, что только в 3 из 10 изображений являются элементами того же класса, в то время как в остальных 7 примерах возникает ошибка определения класса. Например, в 8-м ряду ближайшим обучающим изображением к голове лошади является красный автомобиль, предположительно из-за сильного чёрного фона. В результате этого, изображение лошади в данном случае будет ошибочно помечено как автомобиль.

Мы не уточнили, как именно мы сравниваем два изображения. Технически изображения представляют собой просто два блока (тензора) размером 32 x 32 x 3. Один из самых простых способов — сравнивать изображения попиксельно и суммировать все разности. Другими словами, если у вас есть два изображения, представленные в виде векторов $I_1$, $I_2$, разумным выбором для их сравнения может быть расстояние L1:

$$ d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 - I^p_2 \right| $$

Сумма берется по всем пикселям. Вот как выглядит эта процедура:

Пример использования попиксельных различий для сравнения двух изображений с помощью расстояния $L_1$ (в данном примере для одного цветового канала). Два изображения вычитаются поэлементно, а затем все различия суммируются до получения одного числа. Если два изображения идентичны, результат будет равен нулю. Но если изображения сильно отличаются, результат будет большим.

Давайте также посмотрим, как можно реализовать классификатор в коде. Сначала загрузим данные CIFAR-10 в память в виде четырех массивов: обучающие данные/метки и тестовые данные/метки. В приведенном ниже коде Xtr хранятся все изображения из обучающей выборки (объем 50 000 x 32 x 32 x 3), а соответствующий одномерный массив Ytr (длиной 50 000) содержит обучающие метки (от 0 до 9):

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional 
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072 

Теперь, когда все изображения вытянуты в ряд, мы можем обучить и оценить классификатор:

nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

Обратите внимание, что в качестве критерия оценки обычно используется метрика accuracy, Эта метрика измеряет долю правильных прогнозов в тестовой выборке. Обратите внимание, что все классификаторы, которые мы создадим, имеют общий интерфейс (API). У них есть метод train(X,y), который принимает на вход данные и метки для обучения. Внутри класса должна быть построена своего рода модель, которая предсказывает метки на основе данных. Метод predict(X) принимает новые данные и предсказывает метки.

Пример реализации простого классификатора ближайшего соседа с расстоянием $L_1$, который реализует интерфейс классификатора:

import numpy as np

class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, y):
    """ X is N x D where each row is an example. Y is 1-dimension of size N
        The nearest neighbor classifier simply remembers all the training data """
        self.Xtr = X
        self.ytr = y

    def predict(self, X):
    """ X is N x D where each row is an example we wish to predict label for """
        num_test = X.shape[0]
        # lets make sure that the output type matches the input type
        Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

        # loop over all test rows
        for i in range(num_test):
        # find the nearest training image to the i'th test image
        # using the L1 distance (sum of absolute value differences)
        distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
        min_index = np.argmin(distances) # get the index with smallest distance
        Ypred[i] = self.ytr[min_index] # predict the label of the nearest example

        return Ypred

Если вы запустите этот код, то увидите, что классификатор достигает точности 38,6% на тестовой выборке CIFAR-10. Это более впечатляющий результат, чем случайное угадывание (которое дало бы 10% точности для 10 классов). Но он далёк от результатов человека, которые оцениваются примерно в 94%. Еще лучший результат можно получить с помощью свёрточных нейронных сетей, которые достигают примерно 95% (см. таблицу соревнования Kaggle по CIFAR-10).

Выбор расстояния. Существует множество других способов вычисления расстояний между векторами. Одним из распространённых вариантов может быть использование расстояния $L_2$, которое имеет геометрическую интерпретацию вычисления евклидова расстояния между двумя векторами. Формула для вычисления этого расстояния имеет вид:

$$ d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2} $$

Другими словами, мы вычисляем разницу по пикселям, как и раньше, но на этот раз возводим их в квадрат, складываем и, наконец, извлекаем квадратный корень. Используя приведенный выше код с numpy, нам нужно заменить только одну строку:

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

Обратите внимание на вычисление корня в функции np.sqrt. В практической реализации метода ближайшего соседа мы могли бы не использовать операцию извлечения квадратного корня, потому что он является монотонной функцией. То есть он масштабирует абсолютные значения расстояний, но сохраняет порядок. Поэтому с ним или без него, ближайшие соседи будут идентичны. Однако если применить классификатор ближайшего соседа к CIFAR-10 с $L_2$ расстоянием, получится всего 35,4% точности. Это немного ниже, чем результат с расстоянием $L_1$.

Расстояние $L_1$ против $L_2$ . Различие между этими двумя метриками в том, что расстояние $L_2$ более строгое, чем расстояние $L_1$. Это значит, что если имеется множество небольших расхождений и всего одно большое, расстояние $L_2$ будет больше, чем $L_1$. Понятия расстояний $L_1$ и $L_2$ эквивалентно нормам, которые являются частными случаями p-нормы.

Классификатор k - ближайших соседей

Когда мы хотим сделать более точный прогноз, нам не обязательно использовать только одну метку ближайшего изображения. Действительно, почти всегда можно добиться лучшего результата, используя так называемый классификатор k-ближайших соседей. Идея очень проста: вместо того, чтобы искать одно ближайшее изображение в обучающем наборе, мы найдём k ближайших изображений. Дальше мы сравним их и устроим "голосование" за метку тестового изображения. В частности, когда k = 1, мы получаем классификатор ближайшего соседа. Интуитивно понятно, что чем больше значений k мы возьмем, тем больше будет сглаживающий эффект. Это первый пример гиперпараметра, который делает классификатор более устойчивым к ошибкам:

Пример разницы между классификатором «один ближайший сосед» и классификатором «ближайшие 5 соседей» с использованием двумерных точек и 3 классов (красный, синий, зелёный). Цветные области показывают границы решений, создаваемые классификатором с использованием расстояния $L_2$. Белые области показывают точки, которые классифицируются неоднозначно - голоса за классы равны как минимум для двух классов. Обратите внимание, что в случае классификатора 1-соседа ошибки создают небольшие островки вероятных неверных прогнозов. Например, зелёная точка в середине облака синих точек. В это же время классификатор 5-соседей сглаживает эти неровности, что, приводит к лучшему обобщению на тестовых данных. Также обратите внимание, что серые области на изображении 5-соседей вызваны равенством голосов ближайших соседей. Например, 2 соседа красные, следующие два соседа синие, последний сосед зелёный.

На практике почти всегда используется метод k-ближайших соседей. Но какое значение k следует использовать? Давайте рассмотрим этот вопрос поподробнее.

Наборы данных и настройки гиперпараметров

Классификатор k-ближайших соседей требует настройки параметра k. Интуитивно можно предположить, что существует число, которое подходит лучше всего. Кроме того, мы увидели, что существует множество различных функций расстояния, которые мы могли бы использовать: норма $L_1$, норма $L_2$, а также множество других вариантов, которые мы даже не рассматривали (например, скалярные произведения). Эти варианты называются гиперпараметрами, и они очень часто используются при разработке многих алгоритмов машинного обучения, которые обучаются на данных. Часто не очевидно, какие значения/настройки следует выбрать.

У вас может возникнуть соблазн предложить попробовать множество различных значений и посмотреть, что работает лучше всего. Это хорошая идея, и именно это мы и сделаем, но делать это нужно очень осторожно. В частности, мы не можем использовать тестовый набор данных для настройки гиперпараметров. Всякий раз, когда вы разрабатываете алгоритмы машинного обучения, вы должны относиться к тестовому набору данных как к очень ценному ресурсу, к которому, в идеале, не следует прикасаться до самого конца. В противном случае существует реальная опасность того, что вы настроите гиперпараметры так, чтобы они хорошо работали на тестовом наборе данных, но при развёртывании модели показывали значительное снижение производительности. На практике можно сказать, что произошло переобучение на тестовом наборе данных. С другой стороны, если вы настраиваете гиперпараметры на тестовом наборе данных, вы фактически используете тестовый набор данных в качестве обучающего. По этой причине точность, которую вы достигаете на нём, будет слишком оптимистичной по сравнению с тем, что будет наблюдаться на реальных данных при развёртывании модели. Но если вы используете тестовый набор данных только один раз в конце, он остаётся хорошим показателем для того, чтобы измерить степень обобщения вашего классификатора.

Итого: Оценивайте модель на тестовой выборке только один раз, в самом конце!

Существует правильный способ настройки гиперпараметров, который никак не затрагивает тестовый набор данных. Идея состоит в том, чтобы разделить обучающую выборку на две части: немного меньший обучающий набор и то, что называется выборкой для валидации. Используя в качестве примера CIFAR-10, мы могли бы использовать 49 000 обучающих изображений для обучения и оставить 1000 для валидации. Этот набор данных по сути используется для настройки гиперпараметров.

Вот как это может выглядеть в случае CIFAR-10:

# assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
# recall Xtr_rows is 50,000 x 3072 matrix
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
Ytr = Ytr[1000:]

# find hyperparameters that work best on the validation set
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:

# use a particular value of k and evaluation on validation data
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
# here we assume a modified NearestNeighbor class that can take a k as input
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)

# keep track of what works on the validation set
validation_accuracies.append((k, acc))

По завершении этой процедуры построим график, который показывает, какие значения k работают лучше всего. Затем мы остановимся на этом значении и проведем оценку на реальном тестовом наборе данных.

Разделите обучающую выборку на обучающую и валидационную. Используйте проверочную выборку для настройки всех гиперпараметров. В конце выполните один запуск на тестовой выборке и оцените производительность.

Кросс-валидация. В случаях, когда размер обучающих данных (и, следовательно, проверочных данных) может быть небольшим, люди иногда используют более сложный метод настройки гиперпараметров, называемый кросс-валидацией.

Если вернуться к нашему предыдущему примеру, то идея заключается в том, что вместо произвольного выбора первых 1000 точек данных в качестве проверочного набора, а остальных — в качестве обучающего, можно получить более точную и менее зашумлённую оценку того, насколько хорошо работает определённое значение k, перебирая различные проверочные наборы и усредняя результаты по ним. Например, при 5-кратной перекрёстной проверке мы разделили бы обучающие данные на 5 равных частей, использовали 4 из них для обучения, а 1 — для проверки. Затем мы бы определили, какая из выборок является контрольной, оценили бы производительность и, наконец, усреднили бы производительность по разным выборкам.

Пример 5-кратного выполнения перекрестной проверки для параметра k. Для каждого значения k мы тренируемся на 4 сгибах и оцениваем на 5-м. Следовательно, для каждого k мы получаем 5 значений точности для проверочного сгиба (точность отражается на оси y, и каждый результат равен точке). Линия тренда проводится через среднее значение результатов для каждого k, а столбики ошибок указывают на стандартное отклонение. Обратите внимание, что в данном конкретном случае перекрёстная проверка показывает, что значение около k = 7 лучше всего подходит для этого конкретного набора данных (соответствует пику на графике). Если бы мы использовали более 5 циклов, то могли бы ожидать более плавную (то есть менее шумную) кривую.

На практике люди предпочитают избегать перекрёстной проверки в пользу одного проверочного набора данных, поскольку перекрёстная проверка может быть ресурсозатратной. Обычно люди используют от 50% до 90% обучающих данных для обучения и остальную часть для проверки. Однако это зависит от множества факторов: например, если количество гиперпараметров велико, вы можете предпочесть использовать более крупные проверочные наборы данных. Если количество примеров в проверочном наборе невелико (возможно, всего несколько сотен или около того), безопаснее использовать перекрёстную проверку. На практике обычно используется 3-кратная, 5-кратная или 10-кратная перекрёстная проверка.

Обычное разделение данных. Выделяются обучающий и тестовый наборы данных. Обучающий набор данных делится на части (например, здесь их 5). Части 1-4 становятся обучающим набором данных. Одна часть (например, часть 5, выделенная здесь жёлтым цветом) называется проверочной частью и используется для настройки гиперпараметров. Перекрёстная проверка идёт дальше и позволяет выбрать, какая часть будет проверочной, отдельно от частей 1-5. Это называется 5-кратной перекрёстной проверкой. В самом конце, когда модель обучена и определены все наилучшие гиперпараметры, модель один раз оценивается на тестовых данных (красный цвет).

Плюсы и минусы классификатора ближайших соседей.

Стоит рассмотреть некоторые преимущества и недостатки классификатора «ближайший сосед». Очевидно, что одним из преимуществ является простота реализации и понимания. Кроме того, обучение классификатора не занимает много времени, поскольку всё, что требуется, — это хранить и, возможно, индексировать обучающие данные. Однако мы платим за это вычислительными затратами во время тестирования, поскольку для классификации тестового примера требуется сравнение с каждым обучающим примером. Это неправильно, поскольку на практике мы часто уделяем больше внимания эффективности во время тестирования, чем во время обучения. На самом деле, объемные нейронные сети, которые мы будем разрабатывать в этом классе, смещают этот компромисс в другую крайность: их обучение обходится очень дорого, но после завершения обучения классифицировать новый тестовый пример очень дёшево. Такой режим работы гораздо более желателен на практике.

Кроме того, вычислительная сложность классификатора «ближайший сосед» является активной областью исследований, и существует несколько алгоритмов и библиотек приблизительного поиска ближайшего соседа (ANN), которые могут ускорить поиск ближайшего соседа в наборе данных (например, FLANN ). Эти алгоритмы позволяют найти компромисс между точностью поиска ближайшего соседа и его пространственной/временной сложностью во время поиска и обычно полагаются на этап предварительной обработки/индексирования, который включает в себя построение KD-дерева или запуск алгоритма k-средних.

В некоторых случаях классификатор ближайших соседей может быть хорошим выбором (особенно если данные имеют низкую размерность), но он редко подходит для использования в практических задачах классификации изображений. Одна из проблем заключается в том, что изображения — это объекты с высокой размерностью (то есть они часто содержат много пикселей), а расстояния в многомерных пространствах могут быть очень нелогичными. На изображении ниже показано, что сходство на основе пикселей, которое мы описали выше, сильно отличается от сходства с точки зрения восприятия:

Расстояния на основе пикселей в многомерных данных (и особенно в изображениях) могут быть очень неинтуитивными. Исходное изображение (слева) и три других изображения рядом с ним, которые находятся на одинаковом расстоянии от него на основе пиксельного расстояния $L_2$. Очевидно, что пиксельное расстояние никак не соответствует перцептивному или семантическому сходству.

Вот ещё одна визуализация, которая убедит вас в том, что использование разницы в пикселях для сравнения изображений недостаточно. Мы можем использовать метод визуализации под названием t-SNE, чтобы взять изображения CIFAR-10 и разместить их в двух измерениях так, чтобы их парные (локальные) расстояния сохранялись наилучшим образом. В этой визуализации изображения, которые показаны рядом, считаются очень близкими в соответствии с расстоянием $L_2$ по пикселям, которое мы разработали выше:

Изображения CIFAR-10, размещённые в двух измерениях с помощью t-SNE. Изображения, расположенные рядом на этом изображении, считаются близкими на основе пиксельного расстояния $L_2$. Обратите внимание на сильное влияние фона, а не семантических различий между классами. Нажмите здесь, чтобы увидеть увеличенную версию этой визуализации.

В частности, обратите внимание, что изображения, расположенные друг рядом с другом, в большей степени зависят от общего цветового распределения изображений или типа фона, а не от их семантической идентичности. Например, собаку можно увидеть рядом с лягушкой, потому что они обе находятся на белом фоне. В идеале мы хотели бы, чтобы изображения всех 10 классов образовывали собственные кластеры, чтобы изображения одного класса находились рядом друг с другом независимо от нерелевантных характеристик и вариаций (например, фона). Однако, чтобы добиться этого, нам придётся выйти за рамки необработанных пикселей.

Применение kNN на практике

Подводя итог: - Мы рассмотрели задачу классификации изображений, в которой нам даётся набор изображений, каждое из которых помечено одной категорией. Затем нас просят предсказать эти категории для нового набора тестовых изображений и оценить точность прогнозов. - Мы представили простой классификатор под названием «классификатор ближайших соседей». Мы увидели, что существует множество гиперпараметров (например, значение k или тип расстояния, используемого для сравнения примеров), связанных с этим классификатором, и что не существует очевидного способа их выбора. - Мы увидели, что правильный способ задать эти гиперпараметры — разделить обучающие данные на две части: обучающий набор и поддельный тестовый набор, который мы называем набором для проверки. Мы пробуем разные значения гиперпараметров и оставляем те, которые обеспечивают наилучшую производительность на наборе для проверки. - Если вас беспокоит нехватка обучающих данных, мы обсудили процедуру под названием перекрёстная проверка, которая может помочь уменьшить погрешность при оценке наиболее эффективных гиперпараметров. - Как только мы находим оптимальные гиперпараметры, мы фиксируем их и проводим одну оценку на реальном тестовом наборе данных. - Мы увидели, что метод ближайшего соседа может обеспечить нам точность около 40% на CIFAR-10. Он прост в реализации, но требует хранения всего обучающего набора данных, и его сложно оценивать на тестовых изображениях. - В итоге мы увидели, что использование расстояний $L_1$ или $L_2$ по необработанным значениям пикселей нецелесообразно, поскольку эти расстояния сильнее коррелируют с фоном и цветовыми распределениями изображений, чем с их семантическим содержанием.

На следующих лекциях мы приступим к решению этих задач и в конечном итоге придём к решениям, которые обеспечат точность 90%, позволят полностью отказаться от обучающего набора данных после завершения обучения и позволят оценивать тестовые изображения менее чем за миллисекунду.

Если вы хотите применить kNN на практике (не на изображениях), действуйте следующим образом:

1. Предварительная обработка данных. Нормализуйте признаки в ваших данных (например, один пиксель на изображениях), чтобы среднее значение было равно нулю, а дисперсия — единице. Мы рассмотрим этот прием более подробно в следующих разделах. Сейчас нормализация данных не используется, потому что распределение яркости пикселей на изображениях достаточно однородны.

2. Рассмотрите возможность снижения размерности данных. На практике для снижения размерности используются следующие методы:

3. метод главных компонент ссылка на вики-страницу, ссылка на CS229, ссылка на блог,
4. метод независимых компонент ссылка на вики-страницу, ссылка на блог

5. случайные проекции.

6. Разделите обучающие данные случайным образом на обучающую и проверочную (валидационную) выборки. Как правило, в обучающую выборку попадает от 70 до 90% данных. Этот параметр зависит от того, сколько у вас гиперпараметров и насколько сильно они влияют на результат. Если нужно оценить множество гиперпараметров, лучше использовать более крупную проверочную выборку для их эффективной оценки. Если вас беспокоит размер проверочной выборки, лучше разделить обучающие данные на части и выполнить кросс-валидацию.

7. Обучите и оцените классификатор kNN на кросс-валидации. По возможности выполняйте кросс-валидацию для множества вариантов k и для разных типов расстояний ($L_1$ и $L_2$ — хорошие кандидаты).
   Если вы можете позволить себе потратить больше времени на вычисления, всегда безопаснее использовать кросс-валидацию. Чем больше циклов обучения пройдет, тем лучше, но тем дороже с точки зрения вычислений.

8. Оцените задержку классификатора. Если ваш классификатор kNN работает слишком долгo, рассмотрите возможность использования библиотеки приближённых ближайших соседей. Например, библиотека FLANN позволяет ускорить поиск за счёт некоторой потери точности.

9. Обратите внимание на гиперпараметры, которые дали наилучшие результаты. Возникает вопрос, следует ли использовать валидационный набор для финального обучения с наилучшими гиперпараметрами. Дело в том, что добавить данные для валидации в набор обучающих данных, оптимальные гиперпараметры могут измениться, поскольку размер данных увеличится. На практике лучше не использовать данные валидации в итоговом классификаторе и считать их потерянными при оценке гиперпараметров.

10. Оцените наилучшую модель на тестовом наборе данных. Вычислите точность на тестовой выборке и объявите результат производительностью классификатора kNN на ваших данных.

Дополнительные материалы

Вот несколько дополнительных ссылок, которые могут быть интересными для дальнейшего чтения:
- Несколько полезных фактов о машинном обучении, особенно раздел 6, но рекомендуется к прочтению вся статья.
- Распознавание и изучение категорий объектов, краткий курс по категоризации объектов на ICCV 2005.