Классификация изображений

В этой лекции мы познакомимся с проблемой классификации изображений. Решение проблемы заключается в подходе, основанном на большом объеме размеченных данных.

Содержание:
- Введение в классификацию изображений
- Классификатор ближайшего соседа
- Классификатор k - ближайших соседей
- Наборы данных для настройки гиперпараметров
- Применение kNN на практике
- Дополнительные материалы

Введение в классификацию изображений

Мотивация. В этом разделе мы рассмотрим задачу классификации изображений. Задача заключается в присвоении входному изображению одной метки из фиксированного набора категорий. Это одна из основных задач компьютерного зрения, которая, несмотря на свою простоту, имеет множество практических применений. Более того, многие другие задачи компьютерного зрения (детекция объектов, сегментация) могут быть сведены к классификации изображений.

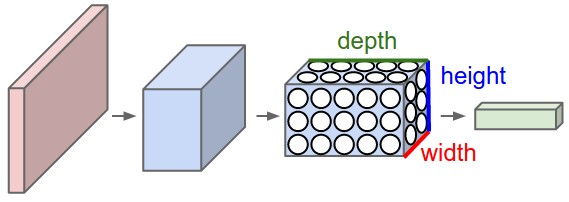
Пример. Например, на изображении ниже модель классификации изображений принимает одно изображение и присваивает вероятности четырём меткам: {«кошка», «собака», «шляпа», «кружка»}. Как показано на изображении, для компьютера изображение представляет собой один большой трёхмерный массив чисел. В этом примере изображение кошки имеет ширину 248 пикселей, высоту 400 пикселей и три цветовых канала: красный, зелёный, синий (или сокращённо RGB). Таким образом, изображение состоит из 248 x 400 x 3 чисел, или в общей сложности 297 600 чисел. Каждое число представляет собой целое число от 0 (чёрный) до 255 (белый). Наша задача — превратить эти четверть миллиона чисел в одну метку, например «кошка».

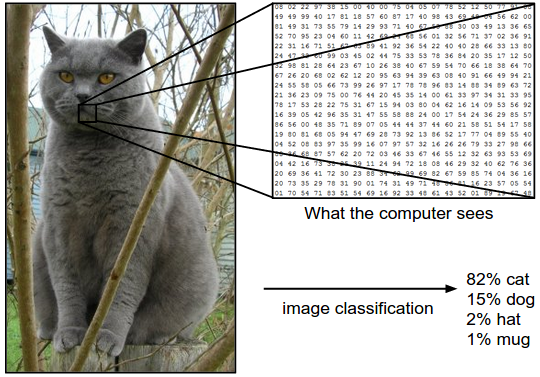
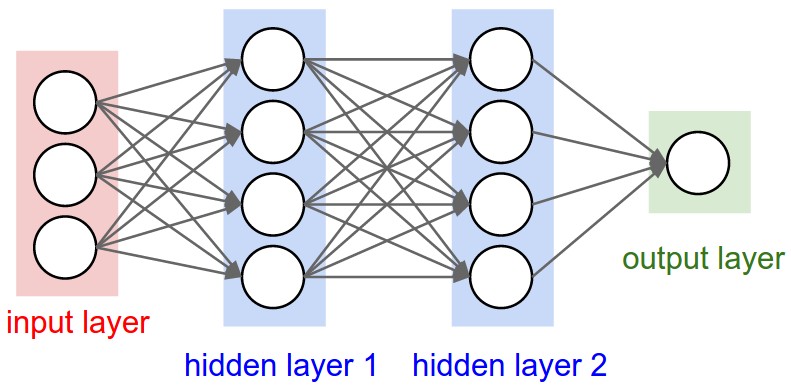
Задача классификации изображений состоит в том, чтобы предсказать одну метку для заданного изображения. Так же мы можем предсказать распределение вероятностей для всех меток, что отражает степень нашей уверенности в результате классификации. Изображения представляют собой трёхмерные массивы целых чисел от 0 до 255 размером «ширина x высота x 3». Число 3 обозначает три цветовых канала: красный, зелёный и синий.

Проблемы. Поскольку задача распознавания визуального образа (например, кошки) относительно проста для человека, стоит рассмотреть связанные с ней проблемы с точки зрения алгоритма компьютерного зрения.
Ниже мы приводим (неполный) список проблем, не забывая о том, что изображения представлены в виде трёхмерного массива значений яркости:
- Изменение точки обзора. Один экземпляр объекта может быть ориентирован по-разному относительно камеры.
- Изменение масштаба. Визуальные классы часто различаются по размеру (размеру в реальном мире, а не только по размеру на изображении).
- Деформация. Многие интересующие нас объекты не являются твёрдыми телами и могут сильно деформироваться.
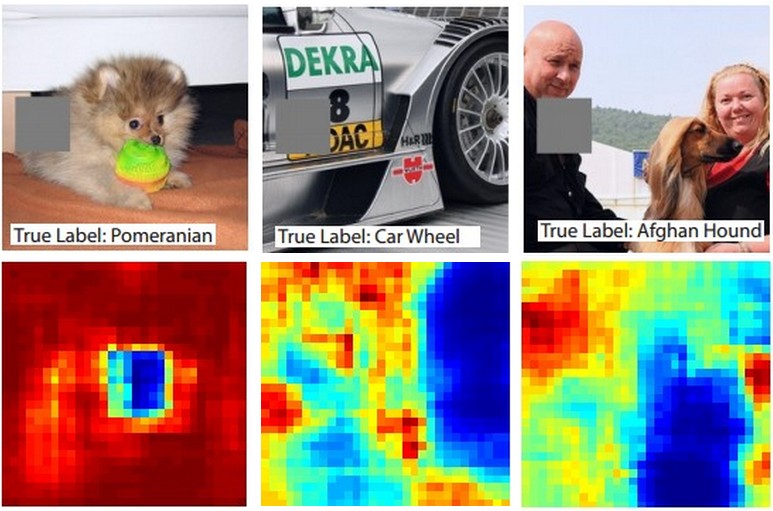
- Окклюзия. Интересующие нас объекты могут быть частично скрыты. Иногда видна лишь небольшая часть объекта (всего несколько пикселей).
- Условия освещения. Влияние освещения на пиксели очень велико.
- Фоновый шум. Интересующие нас объекты могут сливаться с окружающей средой, что затрудняет их идентификацию.
- Внутриклассовые различия. Классы, представляющие интерес, часто могут быть относительно обширными, например, стулья. Существует множество различных типов этих предметов, каждый из которых имеет отличный от других элементов класса внешний вид.

Хорошая модель классификации изображений должна быть инвариантна к перекрёстному произведению всех этих вариаций, сохраняя при этом чувствительность к межклассовым вариациям.

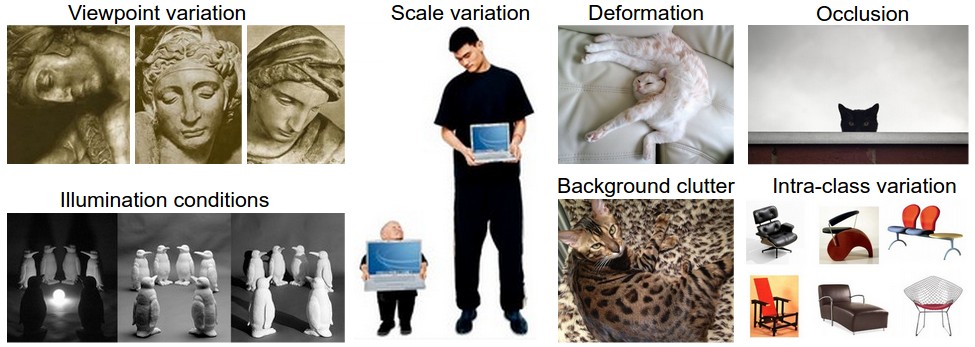
Подход, основанный на данных. Как бы мы могли написать алгоритм, который сможет классифицировать изображения по отдельным категориям? В отличие от написания алгоритма, например, для сортировки списка чисел, не очевидно, как можно написать алгоритм для распознавания кошек на изображениях. Поэтому вместо того, чтобы пытаться описать каждую из интересующих нас категорий непосредственно в коде, мы воспользуемся подходом, похожим на обучение ребёнка. Мы предоставим компьютеру множество примеров, а затем используем алгоритм обучения, который связывает визуальное представление с меткой каждого класса. Этот подход предполагает, что у нас есть обучающий набор с размеченными изображениями. Вот пример того, как может выглядеть такой набор данных:

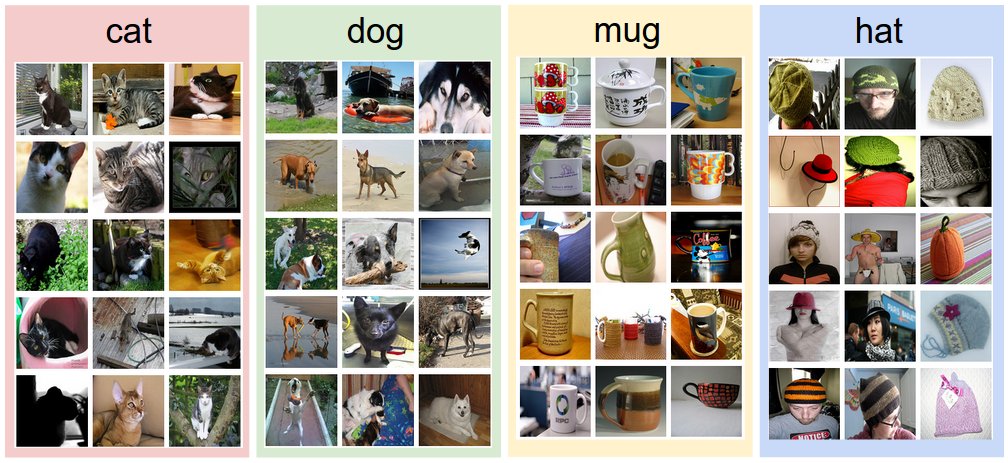
Пример обучающего набора для четырёх визуальных категорий. На практике у нас могут быть тысячи категорий и сотни тысяч изображений для каждой категории.

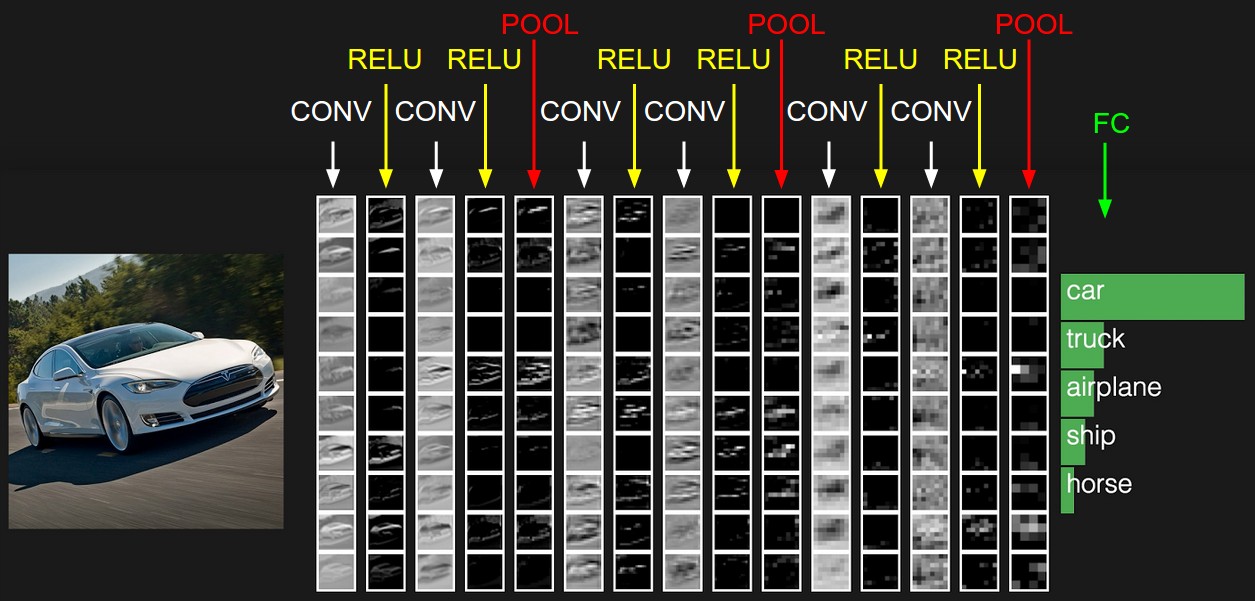
Конвейер классификации изображений. Мы увидели, что задача классификации изображений состоит в том, чтобы взять массив пикселей изображения и присвоить ему метку. Наш полный конвейер можно формализовать следующим образом:
- Входные данные: состоят из набора N изображений, каждое из которых помечено одним из K различных классов. Эти данные называются обучающей выборкой.
- Обучение: наша задача использовать обучающую выборку, чтобы узнать, как выглядит каждый из классов. Мы называем этот этап обучением классификатора или обучением модели.
- Оценка: в конце мы оцениваем качество классификатора. Для этого нужно задать вопрос о том, какие метки предскажет классификатор для нового набора изображений, которые он никогда раньше не видел. Затем мы сравниваем истинные метки этих изображений с теми, которые предсказал классификатор. Интуитивно мы надеемся, что многие прогнозы совпадут с истинными ответами. Данные, которые используются для оценки точности классификатора называются тестовой выборкой.

Классификатор ближайшего соседа

В качестве первого подхода мы используем так называемый классификатор ближайшего соседа. Этот классификатор не имеет ничего общего со свёрточными нейронными сетями и очень редко используется на практике. Однако он позволит нам получить представление о том, как решается задача классификации изображений.

Пример набора данных для классификации изображений: CIFAR-10.
Одним из популярных наборов данных для классификации изображений является набор данных CIFAR-10. Этот набор данных состоит из 60 000 крошечных изображений высотой и шириной 32 пикселя. Каждое изображение относится к одному из 10 классов: самолет, автомобиль, птица и т. д. Эти 60 000 изображений разделены на обучающую выборку из 50 000 изображений и тестовую выборку из 10 000 изображений. На изображении ниже вы можете увидеть 10 случайных примеров изображений для каждого класса.

Слева: примеры изображений из набора данных CIFAR-10.
Справа: в первом столбце показаны несколько тестовых изображений.
Рядом с каждым изображением мы видим 10 наиболее похожих "картинок" из обучающей выборки.

Изначально, у нас есть обучающая выборка CIFAR-10 из 50 000 изображений (по 5000 изображений для каждой из 10 категорий). Мы хотим классифицировать оставшиеся 10 000. Классификатор ближайших соседей работает следующим образом. Берется тестовое изображение и сравается с каждым изображением из обучающей выборки. Будем считать, что метка тестового изображения будет такой же, как и у самого похожего на него изображения.

На изображении выше и справа вы можете увидеть пример результата такой процедуры для 10 тестовых изображений. Обратите внимание, что только в 3 из 10 изображений являются элементами того же класса, в то время как в остальных 7 примерах возникает ошибка определения класса. Например, в 8-м ряду ближайшим обучающим изображением к голове лошади является красный автомобиль, предположительно из-за сильного чёрного фона. В результате этого, изображение лошади в данном случае будет ошибочно помечено как автомобиль.

Мы не уточнили, как именно мы сравниваем два изображения. Технически изображения представляют собой просто два блока (тензора) размером 32 x 32 x 3. Один из самых простых способов — сравнивать изображения попиксельно и суммировать все разности. Другими словами, если у вас есть два изображения, представленные в виде векторов $I_1$, $I_2$, разумным выбором для их сравнения может быть расстояние L1:

$$ d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 - I^p_2 \right| $$

Сумма берется по всем пикселям. Вот как выглядит эта процедура:

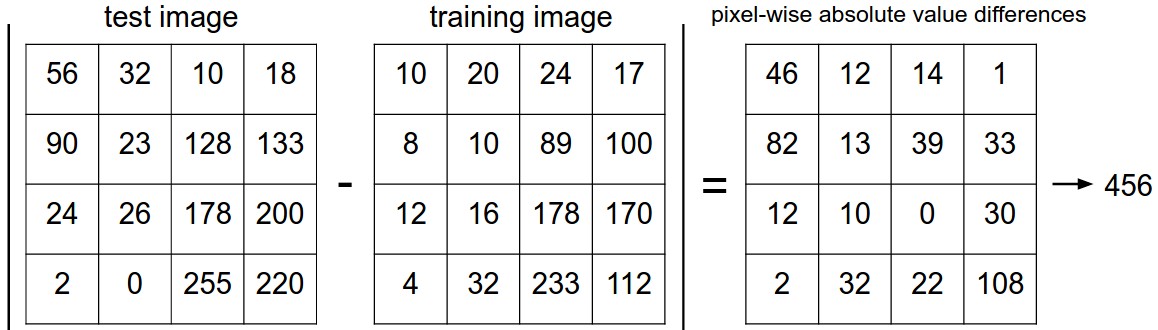
Пример использования попиксельных различий для сравнения двух изображений с помощью расстояния $L_1$ (в данном примере для одного цветового канала). Два изображения вычитаются поэлементно, а затем все различия суммируются до получения одного числа. Если два изображения идентичны, результат будет равен нулю. Но если изображения сильно отличаются, результат будет большим.

Давайте также посмотрим, как можно реализовать классификатор в коде. Сначала загрузим данные CIFAR-10 в память в виде четырех массивов: обучающие данные/метки и тестовые данные/метки. В приведенном ниже коде Xtr хранятся все изображения из обучающей выборки (объем 50 000 x 32 x 32 x 3), а соответствующий одномерный массив Ytr (длиной 50 000) содержит обучающие метки (от 0 до 9):

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional 
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072

Теперь, когда все изображения вытянуты в ряд, мы можем обучить и оценить классификатор:

nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

Обратите внимание, что в качестве критерия оценки обычно используется метрика accuracy, Эта метрика измеряет долю правильных прогнозов в тестовой выборке. Обратите внимание, что все классификаторы, которые мы создадим, имеют общий интерфейс (API). У них есть метод train(X,y), который принимает на вход данные и метки для обучения. Внутри класса должна быть построена своего рода модель, которая предсказывает метки на основе данных. Метод predict(X) принимает новые данные и предсказывает метки.

Пример реализации простого классификатора ближайшего соседа с расстоянием $L_1$, который реализует интерфейс классификатора:

import numpy as np

class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, y):
    """ X is N x D where each row is an example. Y is 1-dimension of size N
        The nearest neighbor classifier simply remembers all the training data """
        self.Xtr = X
        self.ytr = y

    def predict(self, X):
    """ X is N x D where each row is an example we wish to predict label for """
        num_test = X.shape[0]
        # lets make sure that the output type matches the input type
        Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

        # loop over all test rows
        for i in range(num_test):
        # find the nearest training image to the i'th test image
        # using the L1 distance (sum of absolute value differences)
        distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
        min_index = np.argmin(distances) # get the index with smallest distance
        Ypred[i] = self.ytr[min_index] # predict the label of the nearest example

        return Ypred

Если вы запустите этот код, то увидите, что классификатор достигает точности 38,6% на тестовой выборке CIFAR-10. Это более впечатляющий результат, чем случайное угадывание (которое дало бы 10% точности для 10 классов). Но он далёк от результатов человека, которые оцениваются примерно в 94%. Еще лучший результат можно получить с помощью свёрточных нейронных сетей, которые достигают примерно 95% (см. таблицу соревнования Kaggle по CIFAR-10).

Выбор расстояния. Существует множество других способов вычисления расстояний между векторами. Одним из распространённых вариантов может быть использование расстояния $L_2$, которое имеет геометрическую интерпретацию вычисления евклидова расстояния между двумя векторами. Формула для вычисления этого расстояния имеет вид:

$$ d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2} $$

Другими словами, мы вычисляем разницу по пикселям, как и раньше, но на этот раз возводим их в квадрат, складываем и, наконец, извлекаем квадратный корень. Используя приведенный выше код с numpy, нам нужно заменить только одну строку:

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

Обратите внимание на вычисление корня в функции np.sqrt. В практической реализации метода ближайшего соседа мы могли бы не использовать операцию извлечения квадратного корня, потому что он является монотонной функцией. То есть он масштабирует абсолютные значения расстояний, но сохраняет порядок. Поэтому с ним или без него, ближайшие соседи будут идентичны. Однако если применить классификатор ближайшего соседа к CIFAR-10 с $L_2$ расстоянием, получится всего 35,4% точности. Это немного ниже, чем результат с расстоянием $L_1$.

Расстояние $L_1$ против $L_2$ . Различие между этими двумя метриками в том, что расстояние $L_2$ более строгое, чем расстояние $L_1$. Это значит, что если имеется множество небольших расхождений и всего одно большое, расстояние $L_2$ будет больше, чем $L_1$. Понятия расстояний $L_1$ и $L_2$ эквивалентно нормам, которые являются частными случаями p-нормы.

Классификатор k - ближайших соседей

Когда мы хотим сделать более точный прогноз, нам не обязательно использовать только одну метку ближайшего изображения. Действительно, почти всегда можно добиться лучшего результата, используя так называемый классификатор k-ближайших соседей. Идея очень проста: вместо того, чтобы искать одно ближайшее изображение в обучающем наборе, мы найдём k ближайших изображений. Дальше мы сравним их и устроим "голосование" за метку тестового изображения. В частности, когда k = 1, мы получаем классификатор ближайшего соседа. Интуитивно понятно, что чем больше значений k мы возьмем, тем больше будет сглаживающий эффект. Это первый пример гиперпараметра, который делает классификатор более устойчивым к ошибкам:

Пример разницы между классификатором «один ближайший сосед» и классификатором «ближайшие 5 соседей» с использованием двумерных точек и 3 классов (красный, синий, зелёный). Цветные области показывают границы решений, создаваемые классификатором с использованием расстояния $L_2$. Белые области показывают точки, которые классифицируются неоднозначно - голоса за классы равны как минимум для двух классов. Обратите внимание, что в случае классификатора 1-соседа ошибки создают небольшие островки вероятных неверных прогнозов. Например, зелёная точка в середине облака синих точек. В это же время классификатор 5-соседей сглаживает эти неровности, что, приводит к лучшему обобщению на тестовых данных. Также обратите внимание, что серые области на изображении 5-соседей вызваны равенством голосов ближайших соседей. Например, 2 соседа красные, следующие два соседа синие, последний сосед зелёный.

На практике почти всегда используется метод k-ближайших соседей. Но какое значение k следует использовать? Давайте рассмотрим этот вопрос поподробнее.

Наборы данных и настройки гиперпараметров

Классификатор k-ближайших соседей требует настройки параметра k. Интуитивно можно предположить, что существует число, которое подходит лучше всего. Кроме того, мы увидели, что существует множество различных функций расстояния, которые мы могли бы использовать: норма $L_1$, норма $L_2$, а также множество других вариантов, которые мы даже не рассматривали (например, скалярные произведения). Эти варианты называются гиперпараметрами, и они очень часто используются при разработке многих алгоритмов машинного обучения, которые обучаются на данных. Часто не очевидно, какие значения/настройки следует выбрать.

У вас может возникнуть соблазн предложить попробовать множество различных значений и посмотреть, что работает лучше всего. Это хорошая идея, и именно это мы и сделаем, но делать это нужно очень осторожно. В частности, мы не можем использовать тестовый набор данных для настройки гиперпараметров. Всякий раз, когда вы разрабатываете алгоритмы машинного обучения, вы должны относиться к тестовому набору данных как к очень ценному ресурсу, к которому, в идеале, не следует прикасаться до самого конца. В противном случае существует реальная опасность того, что вы настроите гиперпараметры так, чтобы они хорошо работали на тестовом наборе данных, но при развёртывании модели показывали значительное снижение производительности. На практике можно сказать, что произошло переобучение на тестовом наборе данных. С другой стороны, если вы настраиваете гиперпараметры на тестовом наборе данных, вы фактически используете тестовый набор данных в качестве обучающего. По этой причине точность, которую вы достигаете на нём, будет слишком оптимистичной по сравнению с тем, что будет наблюдаться на реальных данных при развёртывании модели. Но если вы используете тестовый набор данных только один раз в конце, он остаётся хорошим показателем для того, чтобы измерить степень обобщения вашего классификатора.

Итого: Оценивайте модель на тестовой выборке только один раз, в самом конце!

Существует правильный способ настройки гиперпараметров, который никак не затрагивает тестовый набор данных. Идея состоит в том, чтобы разделить обучающую выборку на две части: немного меньший обучающий набор и то, что называется выборкой для валидации. Используя в качестве примера CIFAR-10, мы могли бы использовать 49 000 обучающих изображений для обучения и оставить 1000 для валидации. Этот набор данных по сути используется для настройки гиперпараметров.

Вот как это может выглядеть в случае CIFAR-10:

# assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
# recall Xtr_rows is 50,000 x 3072 matrix
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
Ytr = Ytr[1000:]

# find hyperparameters that work best on the validation set
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:

# use a particular value of k and evaluation on validation data
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
# here we assume a modified NearestNeighbor class that can take a k as input
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)

# keep track of what works on the validation set
validation_accuracies.append((k, acc))

По завершении этой процедуры построим график, который показывает, какие значения k работают лучше всего. Затем мы остановимся на этом значении и проведем оценку на реальном тестовом наборе данных.

Разделите обучающую выборку на обучающую и валидационную. Используйте проверочную выборку для настройки всех гиперпараметров. В конце выполните один запуск на тестовой выборке и оцените производительность.

Кросс-валидация. В случаях, когда размер обучающих данных (и, следовательно, проверочных данных) может быть небольшим, люди иногда используют более сложный метод настройки гиперпараметров, называемый кросс-валидацией.

Если вернуться к нашему предыдущему примеру, то идея заключается в том, что вместо произвольного выбора первых 1000 точек данных в качестве проверочного набора, а остальных — в качестве обучающего, можно получить более точную и менее зашумлённую оценку того, насколько хорошо работает определённое значение k, перебирая различные проверочные наборы и усредняя результаты по ним. Например, при 5-кратной перекрёстной проверке мы разделили бы обучающие данные на 5 равных частей, использовали 4 из них для обучения, а 1 — для проверки. Затем мы бы определили, какая из выборок является контрольной, оценили бы производительность и, наконец, усреднили бы производительность по разным выборкам.

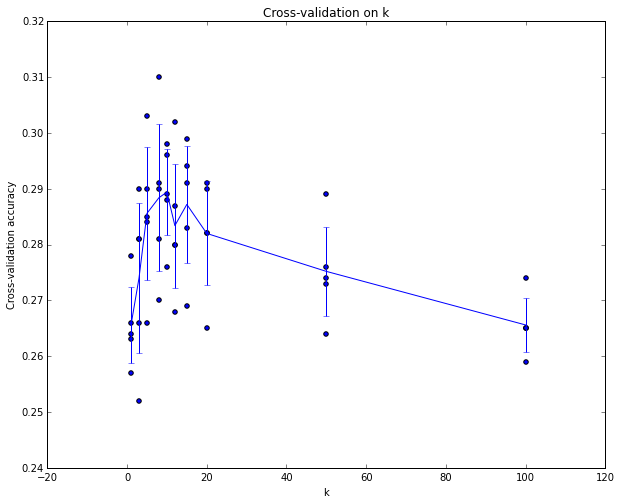
Пример 5-кратного выполнения перекрестной проверки для параметра k. Для каждого значения k мы тренируемся на 4 сгибах и оцениваем на 5-м. Следовательно, для каждого k мы получаем 5 значений точности для проверочного сгиба (точность отражается на оси y, и каждый результат равен точке). Линия тренда проводится через среднее значение результатов для каждого k, а столбики ошибок указывают на стандартное отклонение. Обратите внимание, что в данном конкретном случае перекрёстная проверка показывает, что значение около k = 7 лучше всего подходит для этого конкретного набора данных (соответствует пику на графике). Если бы мы использовали более 5 циклов, то могли бы ожидать более плавную (то есть менее шумную) кривую.

На практике люди предпочитают избегать перекрёстной проверки в пользу одного проверочного набора данных, поскольку перекрёстная проверка может быть ресурсозатратной. Обычно люди используют от 50% до 90% обучающих данных для обучения и остальную часть для проверки. Однако это зависит от множества факторов: например, если количество гиперпараметров велико, вы можете предпочесть использовать более крупные проверочные наборы данных. Если количество примеров в проверочном наборе невелико (возможно, всего несколько сотен или около того), безопаснее использовать перекрёстную проверку. На практике обычно используется 3-кратная, 5-кратная или 10-кратная перекрёстная проверка.

Обычное разделение данных. Выделяются обучающий и тестовый наборы данных. Обучающий набор данных делится на части (например, здесь их 5). Части 1-4 становятся обучающим набором данных. Одна часть (например, часть 5, выделенная здесь жёлтым цветом) называется проверочной частью и используется для настройки гиперпараметров. Перекрёстная проверка идёт дальше и позволяет выбрать, какая часть будет проверочной, отдельно от частей 1-5. Это называется 5-кратной перекрёстной проверкой. В самом конце, когда модель обучена и определены все наилучшие гиперпараметры, модель один раз оценивается на тестовых данных (красный цвет).

Плюсы и минусы классификатора ближайших соседей.

Стоит рассмотреть некоторые преимущества и недостатки классификатора «ближайший сосед». Очевидно, что одним из преимуществ является простота реализации и понимания. Кроме того, обучение классификатора не занимает много времени, поскольку всё, что требуется, — это хранить и, возможно, индексировать обучающие данные. Однако мы платим за это вычислительными затратами во время тестирования, поскольку для классификации тестового примера требуется сравнение с каждым обучающим примером. Это неправильно, поскольку на практике мы часто уделяем больше внимания эффективности во время тестирования, чем во время обучения. На самом деле, объемные нейронные сети, которые мы будем разрабатывать в этом классе, смещают этот компромисс в другую крайность: их обучение обходится очень дорого, но после завершения обучения классифицировать новый тестовый пример очень дёшево. Такой режим работы гораздо более желателен на практике.

Кроме того, вычислительная сложность классификатора «ближайший сосед» является активной областью исследований, и существует несколько алгоритмов и библиотек приблизительного поиска ближайшего соседа (ANN), которые могут ускорить поиск ближайшего соседа в наборе данных (например, FLANN ). Эти алгоритмы позволяют найти компромисс между точностью поиска ближайшего соседа и его пространственной/временной сложностью во время поиска и обычно полагаются на этап предварительной обработки/индексирования, который включает в себя построение KD-дерева или запуск алгоритма k-средних.

В некоторых случаях классификатор ближайших соседей может быть хорошим выбором (особенно если данные имеют низкую размерность), но он редко подходит для использования в практических задачах классификации изображений. Одна из проблем заключается в том, что изображения — это объекты с высокой размерностью (то есть они часто содержат много пикселей), а расстояния в многомерных пространствах могут быть очень нелогичными. На изображении ниже показано, что сходство на основе пикселей, которое мы описали выше, сильно отличается от сходства с точки зрения восприятия:

Расстояния на основе пикселей в многомерных данных (и особенно в изображениях) могут быть очень неинтуитивными. Исходное изображение (слева) и три других изображения рядом с ним, которые находятся на одинаковом расстоянии от него на основе пиксельного расстояния $L_2$. Очевидно, что пиксельное расстояние никак не соответствует перцептивному или семантическому сходству.

Вот ещё одна визуализация, которая убедит вас в том, что использование разницы в пикселях для сравнения изображений недостаточно. Мы можем использовать метод визуализации под названием t-SNE, чтобы взять изображения CIFAR-10 и разместить их в двух измерениях так, чтобы их парные (локальные) расстояния сохранялись наилучшим образом. В этой визуализации изображения, которые показаны рядом, считаются очень близкими в соответствии с расстоянием $L_2$ по пикселям, которое мы разработали выше:

Изображения CIFAR-10, размещённые в двух измерениях с помощью t-SNE. Изображения, расположенные рядом на этом изображении, считаются близкими на основе пиксельного расстояния $L_2$. Обратите внимание на сильное влияние фона, а не семантических различий между классами. Нажмите здесь, чтобы увидеть увеличенную версию этой визуализации.

В частности, обратите внимание, что изображения, расположенные друг рядом с другом, в большей степени зависят от общего цветового распределения изображений или типа фона, а не от их семантической идентичности. Например, собаку можно увидеть рядом с лягушкой, потому что они обе находятся на белом фоне. В идеале мы хотели бы, чтобы изображения всех 10 классов образовывали собственные кластеры, чтобы изображения одного класса находились рядом друг с другом независимо от нерелевантных характеристик и вариаций (например, фона). Однако, чтобы добиться этого, нам придётся выйти за рамки необработанных пикселей.

Применение kNN на практике

Подводя итог: - Мы рассмотрели задачу классификации изображений, в которой нам даётся набор изображений, каждое из которых помечено одной категорией. Затем нас просят предсказать эти категории для нового набора тестовых изображений и оценить точность прогнозов. - Мы представили простой классификатор под названием «классификатор ближайших соседей». Мы увидели, что существует множество гиперпараметров (например, значение k или тип расстояния, используемого для сравнения примеров), связанных с этим классификатором, и что не существует очевидного способа их выбора. - Мы увидели, что правильный способ задать эти гиперпараметры — разделить обучающие данные на две части: обучающий набор и поддельный тестовый набор, который мы называем набором для проверки. Мы пробуем разные значения гиперпараметров и оставляем те, которые обеспечивают наилучшую производительность на наборе для проверки. - Если вас беспокоит нехватка обучающих данных, мы обсудили процедуру под названием перекрёстная проверка, которая может помочь уменьшить погрешность при оценке наиболее эффективных гиперпараметров. - Как только мы находим оптимальные гиперпараметры, мы фиксируем их и проводим одну оценку на реальном тестовом наборе данных. - Мы увидели, что метод ближайшего соседа может обеспечить нам точность около 40% на CIFAR-10. Он прост в реализации, но требует хранения всего обучающего набора данных, и его сложно оценивать на тестовых изображениях. - В итоге мы увидели, что использование расстояний $L_1$ или $L_2$ по необработанным значениям пикселей нецелесообразно, поскольку эти расстояния сильнее коррелируют с фоном и цветовыми распределениями изображений, чем с их семантическим содержанием.

На следующих лекциях мы приступим к решению этих задач и в конечном итоге придём к решениям, которые обеспечат точность 90%, позволят полностью отказаться от обучающего набора данных после завершения обучения и позволят оценивать тестовые изображения менее чем за миллисекунду.

Если вы хотите применить kNN на практике (не на изображениях), действуйте следующим образом:

Предварительная обработка данных. Нормализуйте признаки в ваших данных (например, один пиксель на изображениях), чтобы среднее значение было равно нулю, а дисперсия — единице. Мы рассмотрим этот прием более подробно в следующих разделах. Сейчас нормализация данных не используется, потому что распределение яркости пикселей на изображениях достаточно однородны.
Рассмотрите возможность снижения размерности данных. На практике для снижения размерности используются следующие методы:
метод главных компонент ссылка на вики-страницу, ссылка на CS229, ссылка на блог,
метод независимых компонент ссылка на вики-страницу, ссылка на блог
случайные проекции.
Разделите обучающие данные случайным образом на обучающую и проверочную (валидационную) выборки. Как правило, в обучающую выборку попадает от 70 до 90% данных. Этот параметр зависит от того, сколько у вас гиперпараметров и насколько сильно они влияют на результат. Если нужно оценить множество гиперпараметров, лучше использовать более крупную проверочную выборку для их эффективной оценки. Если вас беспокоит размер проверочной выборки, лучше разделить обучающие данные на части и выполнить кросс-валидацию.
Обучите и оцените классификатор kNN на кросс-валидации. По возможности выполняйте кросс-валидацию для множества вариантов k и для разных типов расстояний ($L_1$ и $L_2$ — хорошие кандидаты).
Если вы можете позволить себе потратить больше времени на вычисления, всегда безопаснее использовать кросс-валидацию. Чем больше циклов обучения пройдет, тем лучше, но тем дороже с точки зрения вычислений.
Оцените задержку классификатора. Если ваш классификатор kNN работает слишком долгo, рассмотрите возможность использования библиотеки приближённых ближайших соседей. Например, библиотека FLANN позволяет ускорить поиск за счёт некоторой потери точности.
Обратите внимание на гиперпараметры, которые дали наилучшие результаты. Возникает вопрос, следует ли использовать валидационный набор для финального обучения с наилучшими гиперпараметрами. Дело в том, что добавить данные для валидации в набор обучающих данных, оптимальные гиперпараметры могут измениться, поскольку размер данных увеличится. На практике лучше не использовать данные валидации в итоговом классификаторе и считать их потерянными при оценке гиперпараметров.
Оцените наилучшую модель на тестовом наборе данных. Вычислите точность на тестовой выборке и объявите результат производительностью классификатора kNN на ваших данных.

Дополнительные материалы

Вот несколько дополнительных ссылок, которые могут быть интересными для дальнейшего чтения:
- Несколько полезных фактов о машинном обучении, особенно раздел 6, но рекомендуется к прочтению вся статья.
- Распознавание и изучение категорий объектов, краткий курс по категоризации объектов на ICCV 2005.

Понимание и визуализация

Андрей Лабинцев

2025-03-13 19:42

Понимание и визуализация

(эта страница в настоящее время находится в черновом варианте)

В литературе было разработано несколько подходов к пониманию и визуализации сверточных сетей, отчасти в ответ на распространенную критику о том, что изученные признаки в нейронной сети не поддаются интерпретации. В этом разделе мы кратко рассмотрим некоторые из этих подходов и связанную с ними работу.

Визуализация активаций и веса первого слоя

Активации слоев. Наиболее простой метод визуализации заключается в том, чтобы показать активации сети во время прямого прохода. В сетях ReLU активации обычно выглядят относительно неровными и плотными, но по мере обучения активации обычно становятся более редкими и локализованными. Одна из опасных ловушек, которую можно легко заметить с помощью этой визуализации, заключается в том, что некоторые карты активации могут быть равны нулю для множества различных входных данных, что может указывать на мертвые фильтры и может быть симптомом высокой скорости обучения.

Типичные активации на первом слое CONV (сверху) и на 5-м слое CONV (снизу) обученного AlexNet смотрят на изображение кошки. В каждом боксе отображается карта активации, соответствующая какому-либо фильтру. Обратите внимание, что активации редкие (большинство значений равны нулю, на этой визуализации показаны черным цветом) и в основном локальные.

Фильтры Conv/FC. Вторая распространенная стратегия заключается в визуализации весов. Обычно они наиболее интерпретируемы на первом слое CONV, который смотрит непосредственно на необработанные пиксельные данные, но также можно показать веса фильтров в более глубоких слоях сети. Весовые коэффициенты полезны для визуализации, потому что хорошо обученные сети обычно отображают красивые и плавные фильтры без каких-либо зашумленных узоров. Зашумленные паттерны могут быть индикатором сети, которая не обучалась достаточно долго, или, возможно, очень низкой интенсивности регуляризации, которая могла привести к переобучению.

Типичные фильтры на первом слое CONV (сверху) и на 2-м слое CONV (снизу) обученного AlexNet. Обратите внимание, что веса первого слоя очень красивые и гладкие, что указывает на хорошо сходящуюся сеть. Функции цвета/оттенков серого сгруппированы, потому что AlexNet содержит два отдельных потока обработки, и очевидным следствием такой архитектуры является то, что один поток развивает высокочастотные элементы оттенков серого, а другой — низкочастотные цветовые функции. Веса 2-го слоя CONV не так легко интерпретируемы, но очевидно, что они все еще гладкие, хорошо сформированные и лишены зашумленных узоров.

Получение изображений, которые максимально активируют нейрон

Еще один метод визуализации заключается в том, чтобы взять большой набор изображений, пропустить их через сеть и отслеживать, какие изображения максимально активируют тот или иной нейрон. Затем мы можем визуализировать изображения, чтобы понять, что нейрон ищет в своем рецептивном поле. Одна из таких визуализаций (среди прочих) показана в статье Богатые иерархии функций для точного обнаружения объектов и семантической сегментации Росса Гиршика и др.:

Максимально активизирующие изображения для некоторых нейронов POOL5 (5-й слой пула) AlexNet. Значения активации и рецептивное поле конкретного нейрона показаны белым цветом. (В частности, обратите внимание, что нейроны POOL5 являются функцией относительно большой части входного изображения!) Можно видеть, что некоторые нейроны реагируют на верхнюю часть тела, текст или зеркальные блики.

Одна из проблем с этим подходом заключается в том, что нейроны ReLU не обязательно имеют какое-либо семантическое значение сами по себе. Скорее, более уместно думать о множественных нейронах ReLU как о базисных векторах некоторого пространства, представленного в виде участков изображения. Другими словами, визуализация показывает участки на краю облака представлений, вдоль (произвольных) осей, которые соответствуют весам фильтра. Это также можно увидеть по тому факту, что нейроны в ConvNet работают линейно над входным пространством, поэтому любое произвольное вращение этого пространства является запретным. Этот момент был далее аргументирован в книге Сегеди и др. «Интригующие свойства нейронных сетей», где они выполняют аналогичную визуализацию вдоль произвольных направлений в пространстве представления.

Встраивание кодов с помощью t-SNE

ConvNet можно интерпретировать как постепенное преобразование изображений в представление, в котором классы разделяются линейным классификатором. Мы можем получить приблизительное представление о топологии этого пространства, встроив изображения в два измерения таким образом, чтобы их низкоразмерное представление имело примерно равные расстояния, чем их высокомерное представление. Существует множество методов вложения, которые были разработаны с помощью интуиции вложения векторов высокой размерности в пространство низкой размерности с сохранением парных расстояний точек. Среди них t-SNE является одним из самых известных методов, который неизменно дает визуально приятные результаты.

Чтобы произвести встраивание, мы можем взять набор изображений и использовать ConvNet для извлечения кодов CNN (например, в AlexNet 4096-мерный вектор прямо перед классификатором, и, что особенно важно, включая нелинейность ReLU). Затем мы можем подключить их к t-SNE и получить двумерный вектор для каждого изображения. Соответствующие изображения могут быть визуализированы в виде сетки:

Встраивание набора изображений в t-SNE на основе их кодов CNN. Изображения, которые находятся рядом друг с другом, также близки в пространстве репрезентации CNN, что подразумевает, что CNN «видит» их как очень похожие. Обратите внимание, что сходства чаще всего основаны на классах и семантике, а не на пикселях и цветах. Для получения более подробной информации о том, как была создана эта визуализация, связанный код, а также другие связанные визуализации в разных масштабах см. Визуализация кодов CNN в t-SNE.

Окклюзия частей изображения

Предположим, что ConvNet классифицирует изображение как собаку. Как мы можем быть уверены, что он на самом деле улавливает собаку на изображении, а не какие-то контекстуальные подсказки на фоне или какой-то другой объект? Одним из способов исследования того, из какой части изображения исходит предсказание классификации, является построение графика вероятности интересующего класса (например, класса собаки) в зависимости от положения объекта-окклюдера. То есть, мы перебираем области изображения, устанавливаем участок изображения равным нулю и смотрим на вероятность класса. Мы можем визуализировать вероятность в виде двумерной тепловой карты. Этот подход был использован в книге Мэтью Цайлера «Визуализация и понимание сверточных сетей»:

Три входных изображения (вверху). Обратите внимание, что окклюдерная область показана серым цветом. Когда мы проводим окклюдером по изображению, мы записываем вероятность правильного класса, а затем визуализируем его в виде тепловой карты (показанной под каждым изображением). Например, на крайнем левом изображении мы видим, что вероятность померанского шпица резко падает, когда окклюдер закрывает морду собаки, что дает нам некоторую степень уверенности в том, что морда собаки в первую очередь ответственна за высокий балл классификации. И наоборот, обнуление других частей изображения имеет относительно незначительное влияние.

Визуализация градиента данных и его друзей

Градиент данных.|

Глубоко внутри сверточных сетей: визуализация моделей классификации изображений и карт заметности

DeconvNet.

Визуализация и понимание сверточных сетей

Управляемое обратное распространение.

Стремление к простоте: Всесвёрточная сеть

Архитектура нейросетей

Андрей Лабинцев

2025-03-12 19:42

Архитектура нейросетей

Содержание: - Обзор архитектуры - Слои ConvNet - Сверточный слой - Слой пула - Слой нормализации - Полностью подключенный слой - Преобразование полносвязных слоев в сверточные слои - Архитектуры ConvNet - Узоры слоев - Шаблоны для определения размеров слоев - Тематические исследования (LeNet / AlexNet / ZFNet / GoogLeNet / VGGNet) - Вычислительные соображения - Дополнительные материалы

Сверточные нейронные сети (CNNs / ConvNets)

Сверточные нейронные сети очень похожи на обычные нейронные сети из предыдущей главы: они состоят из нейронов, которые имеют обучаемые веса и смещения. Каждый нейрон получает некоторые входные данные, выполняет скалярное произведение и опционально следует за ним с нелинейностью. Вся сеть по-прежнему выражает одну дифференцируемую функцию оценки: от пикселей необработанного изображения на одном конце до оценок классов на другом. И у них по-прежнему есть функция потерь (например, SVM/Softmax) на последнем (полностью подключенном) слое, и все советы/рекомендации, которые мы разработали для обучения обычным нейронным сетям, по-прежнему применимы.

Так что же меняется? Архитектуры ConvNet явно предполагают, что входные данные являются изображениями, что позволяет нам закодировать определенные свойства в архитектуре. Это делает функцию forward более эффективной для реализации и значительно сокращает количество параметров в сети.

Обзор архитектуры

Напомним: обычные нейронные сети. Как мы видели в предыдущей главе, нейронные сети получают входные данные (один вектор) и преобразуют их через серию скрытых слоев. Каждый скрытый слой состоит из набора нейронов, где каждый нейрон полностью связан со всеми нейронами предыдущего слоя, и где нейроны в одном слое функционируют совершенно независимо и не имеют общих связей. Последний полносвязный слой называется «выходным слоем» и в настройках классификации представляет собой баллы класса.

Обычные нейронные сети плохо масштабируются до полных изображений. В CIFAR-10 изображения имеют размер всего 32x32x3 (32 в ширину, 32 в высоту, 3 цветных канала), поэтому один полностью связанный нейрон в первом скрытом слое обычной нейронной сети будет иметь 32 * 32 * 3 = 3072 веса. Это количество все еще кажется управляемым, но очевидно, что эта полностью связанная структура не масштабируется до более крупных изображений. Например, изображение более приличного размера, например, 200x200x3, приведет к нейронам с весом 2002003 = 120 000. Более того, мы почти наверняка хотели бы иметь несколько таких нейронов, чтобы параметры быстро складывались! Очевидно, что такая полная связность является расточительной, а огромное количество параметров быстро приведет к переобучению.

3D объемы нейронов. Сверточные нейронные сети используют тот факт, что входные данные состоят из изображений, и они ограничивают архитектуру более разумным образом. В частности, в отличие от обычной нейронной сети, слои ConvNet имеют нейроны, расположенные в трех измерениях: ширина, высота, глубина. (Обратите внимание, что слово «глубина» здесь относится к третьему измерению объема активации, а не к глубине полной нейронной сети, которая может относиться к общему количеству слоев в сети.) Например, входные изображения в CIFAR-10 представляют собой входной объем активаций, а объем имеет размеры 32х32х3 (ширина, высота, глубина соответственно). Как мы вскоре увидим, нейроны в слое будут соединены только с небольшой областью слоя перед ним, а не со всеми нейронами в полном объеме. Более того, итоговый выходной слой для CIFAR-10 будет иметь размеры 1x1x10, так как к концу архитектуры ConvNet мы сведем полное изображение к единому вектору оценок классов, расположенных по размерности глубины. Вот визуализация:

Сверху: обычная 3-слойная нейронная сеть.
Снизу: ConvNet располагает свои нейроны в трех измерениях (ширина, высота, глубина), как это визуализировано в одном из слоев. Каждый слой ConvNet преобразует входной объем 3D в объем активации нейронов на выходе 3D. В этом примере красный входной слой содержит изображение, поэтому его ширина и высота будут соответствовать размерам изображения, а глубина будет равна 3 (красный, зеленый, синий каналы).

ConvNet состоит из слоев. У каждого слоя есть простой API: он преобразует входной 3D-объем в выходной 3D-объем с помощью некоторой дифференцируемой функции, которая может иметь или не иметь параметры.

Слои, используемые для построения ConvNet

Как мы уже описывали выше, простая ConvNet представляет собой последовательность слоев, и каждый слой ConvNet преобразует один объем активаций в другой с помощью дифференцируемой функции. Мы используем три основных типа слоев для построения архитектур ConvNet: сверточный слой, слой пула и полносвязный слой (точно так же, как это видно в обычных нейронных сетях). Мы сложим эти слои, чтобы сформировать полноценную архитектуру ConvNet.

Пример архитектуры: обзор. Мы рассмотрим это более подробно ниже, но простой ConvNet для классификации CIFAR-10 может иметь архитектуру [INPUT - CONV - RELU - POOL - FC]. Более подробно:

INPUT [32x32x3] будет содержать исходные значения пикселей изображения, в данном случае изображение шириной 32, высотой 32 и с тремя цветовыми каналами R,G,B.
Слой CONV будет вычислять выходные данные нейронов, которые соединены с локальными областями на входных данных, каждый из которых вычисляет скалярное произведение между их весами и небольшой областью, к которой они подключены во входном объеме. Это может привести к объему [32x32x12], если мы решили использовать 12 фильтров.
Слой RELU будет применять функцию поэлементной активации, такую как max(0,х) с пороговым значением на нуле. При этом размер тома остается неизменным ([32x32x12]).
Слой POOL выполнит операцию понижения дискретизации вдоль пространственных измерений (ширина, высота), в результате чего будет получен объем, такой как [16x16x12].
Уровень FC (т.е. полностью подключенный) будет вычислять баллы класса, в результате чего будет получен объем размера [1x1x10], где каждое из 10 чисел соответствует баллу класса, например, среди 10 категорий CIFAR-10. Как и в случае с обычными нейронными сетями и как следует из названия, каждый нейрон в этом слое будет связан со всеми числами в предыдущем объеме.

Таким образом, ConvNet слой за слоем преобразуют исходное изображение от исходных значений пикселей до итоговых оценок класса. Обратите внимание, что некоторые слои содержат параметры, а другие нет. В частности, слои CONV/FC выполняют преобразования, которые являются функцией не только активации входного объема, но и параметров (весов и смещений нейронов). С другой стороны, слои RELU/POOL будут реализовывать фиксированную функцию. Параметры в слоях CONV/FC будут обучаться с помощью градиентного спуска, чтобы оценки классов, вычисляемые ConvNet, соответствовали меткам в обучающем наборе для каждого изображения.

Вкратце:

Архитектура ConvNet в простейшем случае представляет собой список слоев, которые преобразуют объем изображения в выходной объем (например, содержат оценки классов)
Существует несколько различных типов слоев (например, CONV/FC/RELU/POOL на сегодняшний день являются наиболее популярными)
Каждый слой принимает входной 3D-объем и преобразует его в выходной 3D-объем с помощью дифференцируемой функции
Каждый слой может иметь или не иметь параметры (например, у CONV/FC есть, у RELU/POOL нет)
Каждый слой может иметь или не иметь дополнительные гиперпараметры (например, у CONV/FC/POOL есть, у RELU нет)

Активация примера архитектуры ConvNet. Начальный том хранит необработанные пиксели изображения (слева), а последний том хранит оценки класса (справа). Каждый объем активаций на пути обработки отображается в виде столбца. Так как визуализировать 3D-объемы сложно, мы выкладываем срезы каждого тома в ряды. Последний объем слоя содержит баллы для каждого класса, но здесь мы визуализируем только отсортированные 5 лучших баллов и печатаем этикетки каждого из них. Полный прототип веб-версии приведен в шапке нашего веб-сайта. Архитектура, показанная здесь, представляет собой крошечную сеть VGG, о которой мы поговорим позже.

Теперь мы опишем отдельные слои и детали их гиперпараметров и связуемости.

Сверточный слой

Уровень Conv является основным строительным блоком сверточной сети, который выполняет большую часть тяжелой вычислительной работы.

Обзор и интуиция без мозгов. Давайте сначала обсудим, что вычисляет слой CONV без аналогий между мозгом и нейронами. Параметры слоя CONV состоят из набора обучаемых фильтров. Каждый фильтр имеет небольшие пространственные размеры (по ширине и высоте), но простирается на всю глубину входного объема. Например, типичный фильтр на первом слое ConvNet может иметь размер 5x5x3 (т. е. 5 пикселей в ширину и высоту, и 3, поскольку изображения имеют глубину 3, цветовые каналы). Во время прямого прохода мы скользим (точнее, свертываем) каждый фильтр по ширине и высоте входного объема и вычисляем точечные произведения между входами фильтра и входом в любом положении. Когда мы перемещаем фильтр по ширине и высоте входного объема, мы создадим двумерную карту активации, которая дает ответы этого фильтра в каждом пространственном положении. Интуитивно сеть будет изучать фильтры, которые активируются, когда они видят какой-либо визуальный признак, такой как край определенной ориентации или пятно определенного цвета на первом слое, или, в конечном итоге, целые соты или узоры, похожие на колеса, на более высоких слоях сети. Теперь у нас будет целый набор фильтров в каждом слое CONV (например, 12 фильтров), и каждый из них создаст отдельную двухмерную карту активации. Мы наложим эти карты активации вдоль измерения глубины и получим выходной объем.

Взгляд на мозг. Если вы являетесь поклонником аналогий между мозгом и нейронами, то каждая запись в 3D-объеме вывода также может быть интерпретирована как выход нейрона, который смотрит только на небольшую область на входе и разделяет параметры со всеми нейронами слева и справа в пространстве (поскольку все эти числа являются результатом применения одного и того же фильтра).

Теперь мы обсудим детали соединений нейронов, их расположение в пространстве и схему совместного использования параметров.

Местная связность. Когда речь идет о многомерных входных данных, таких как изображения, как мы видели выше, нецелесообразно соединять нейроны со всеми нейронами в предыдущем томе. Вместо этого мы будем подключать каждый нейрон только к локальной области входного объема. Пространственная протяженность этой связности является гиперпараметром, называемым рецептивным полем нейрона (эквивалентно размеру фильтра). Степень связности вдоль оси глубины всегда равна глубине входного объема. Важно еще раз подчеркнуть эту асимметрию в том, как мы трактуем пространственные размеры (ширину и высоту) и размеры глубины: соединения локальны в 2D-пространстве (по ширине и высоте), но всегда полны по всей глубине входного объема.

Пример 1. Например, предположим, что входной объем имеет размер [32x32x3] (например, изображение RGB CIFAR-10). Если рецептивное поле (или размер фильтра) равно 5x5, то каждый нейрон в слое Conv будет иметь веса в области [5x5x3] во входном объеме, что в сумме составляет 5x5x3 = 75 весов (и параметр смещения +1). Обратите внимание, что степень связности вдоль оси глубины должна быть равна 3, так как это глубина входного объема.

Пример 2. Предположим, что входной объем имеет размер [16x16x20]. Затем, используя пример с размером рецептивного поля 3x3, каждый нейрон в слое Conv теперь будет иметь в общей сложности 3x3x20 = 180 соединений с входным объемом. Обратите внимание, что, опять же, связность является локальной в 2D-пространстве (например, 3x3), но полной по глубине ввода (20).

Сверху: Пример входного объема красным цветом (например, изображение CIFAR-10 размером 32x32x3) и пример объема нейронов в первом сверточном слое. Каждый нейрон в сверточном слое пространственно связан только с локальной областью во входном объеме, но на всю глубину (т.е. со всеми цветовыми каналами). Обратите внимание, что в глубине есть несколько нейронов (5 в этом примере), все они смотрят на одну и ту же область на входе: линии, которые соединяют этот столбец из 5 нейронов, не представляют веса (т.е. эти 5 нейронов не имеют одинаковых весов, но они связаны с 5 разными фильтрами), они просто указывают на то, что эти нейроны связаны или смотрят на одно и то же рецептивное поле или область входного объема. т.е. они имеют одно и то же рецептивное поле, но не одинаковые веса. Снизу: Нейроны из главы «Нейронные сети» остаются неизменными: они по-прежнему вычисляют скалярное произведение своих весов с последующим нелинейным значением, но их связность теперь ограничена локальными пространственными данными.

Пространственное расположение. Мы объяснили связь каждого нейрона в слое Conv с входным объемом, но мы еще не обсуждали, сколько нейронов находится в выходном объеме или как они организованы. Три гиперпараметра контролируют размер выходного объема: глубина, шаг и нулевое отступление. Мы обсудим их далее:
- Во-первых, глубина выходного объема — это гиперпараметр: он соответствует количеству фильтров, которые мы хотели бы использовать, каждый из которых учится искать что-то свое во входных данных. Например, если первый сверточный слой принимает в качестве входных данных исходное изображение, то различные нейроны в измерении глубины могут активироваться в присутствии различных ориентированных краев или цветовых пятен. Мы будем называть набор нейронов, которые смотрят на одну и ту же область входных данных, столбцом глубины (некоторые люди также предпочитают термин «волокно»). - Во-вторых, мы должны указать шаг, с которым мы перемещаем фильтр. Когда шаг равен 1, мы перемещаем фильтры по одному пикселю за раз. Когда шаг равен 2 (или редко 3 или более, хотя на практике это редкость), фильтры прыгают на 2 пикселя за раз, когда мы их перемещаем. Это позволит производить меньшие объемы выпуска в пространственном отношении. - Как мы скоро увидим, иногда будет удобно заполнять входной объем нулями по границе. Размер этого нулевого отступа является гиперпараметром. Приятная особенность нулевого заполнения заключается в том, что он позволяет нам контролировать пространственный размер выходных объемов (чаще всего, как мы скоро увидим, мы будем использовать его для точного сохранения пространственного размера входного объема, чтобы ширина и высота входного и выходного объема были одинаковыми).

Мы можем вычислить пространственный размер выходного объема как функцию от размера входного объема (W), размер рецептивного поля нейронов Conv слоя (F), шаг, с которым они наносятся (S) и количество использованного нулевого заполнения (P) на границе. Вы можете убедиться в том, что правильная формула для расчета количества нейронов «поместится» по формуле (W−F+2P)/S+1. Например, для входа 7x7 и фильтра 3x3 со stride 1 и pad 0 мы получим выход 5x5. С помощью шага 2 мы получим выход 3x3. Давайте также посмотрим еще на один графический пример:

Иллюстрация пространственного расположения. В этом примере есть только одно пространственное измерение (ось x), один нейрон с размером рецептивного поля F = 3, входной размер W = 5 и нулевое заполнение P = 1. Сверху: Нейрон шагал по входу с шагом S = 1, давая на выходе размер (5 - 3 + 2)/1 + 1 = 5. Снизу: Нейрон использует шаг S = 2, давая выход размера (5 - 3 + 2)/2 + 1 = 3. Обратите внимание, что шаг S = 3 не может быть использован, так как он не будет аккуратно помещаться по объему. С точки зрения уравнения, это можно определить, так как (5 - 3 + 2) = 4 не делится на 3. Веса нейронов в этом примере [1,0,-1] (показаны справа), и их смещение равно нулю. Эти веса являются общими для всех желтых нейронов (см. общие параметры ниже).

Использование нулевой набивки. В приведенном выше примере слева обратите внимание, что входной размер был равен 5, а выходной размер был равен: также 5. Это сработало так, потому что наши рецептивные поля были равны 3, и мы использовали нулевую набивку 1. Если бы не использовалось заполнение нуля, то выходной объем имел бы пространственную размерность только 3, потому что именно столько нейронов «поместилось» бы на исходном входе. Как правило, установка нулевого заполнения равным P=(F−1)/2. Когда шаг S=1 гарантирует, что входной и выходной объем будут иметь одинаковый пространственный размер. Очень часто используется нулевое заполнение таким образом, и мы обсудим все причины, когда будем говорить больше об архитектурах ConvNet.

Ограничения на шаг. Обратите внимание, что гиперпараметры пространственного расположения имеют взаимные ограничения. Например, когда входные данные имеют размер W=10, нулевой отступ не используется P=0, а размер фильтра равен F=3, то использовать stride было бы невозможно S=2__с (W−F+2P)/S+1=(10−3+0)/2+1=4.5__, т.е. не целое число, указывающее на то, что нейроны не «помещаются» аккуратно и симметрично на входе. Таким образом, эта настройка гиперпараметров считается недопустимой, и библиотека ConvNet может выдать исключение или обнулить заполнение оставшейся части, чтобы она поместилась, или обрезать входные данные, чтобы она поместилась, или что-то еще. Как мы увидим в разделе Архитектуры ConvNet, правильный выбор размеров ConvNet, чтобы все размеры «отрабатывались», может стать настоящей головной болью, которую использование нулевого заполнения и некоторые рекомендации по проектированию значительно облегчат.

Пример из жизни. Архитектура Крижевского и др., которая выиграла конкурс ImageNet в 2012 году, принимала изображения размером [227x227x3]. На первом сверточном слое использовались нейроны с размером рецептивного поля F=11__шаг __S=4 и без нулевой набивки P=0. Так как (227 - 11)/4 + 1 = 55, и так как слой Conv имел глубину K=96 , выходной объем слоя Conv имел размер [55x55x96]. Каждый из 55x55x96 нейронов в этом объеме был соединен с областью размера [11x11x3] во входном объеме. Более того, все 96 нейронов в каждой глубинной колонке подключены к одной и той же области входного канала [11x11x3], но, конечно, с разными весами. В качестве забавного отступления, если вы прочитаете реальную статью, она утверждает, что входные изображения были 224x224, что, безусловно, неверно, потому что (224 - 11)/4 + 1 совершенно очевидно не является целым числом. Это сбило с толку многих людей в истории ConvNets, и мало что известно о том, что произошло. Мое собственное предположение заключается в том, что Алекс использовал нулевое заполнение из 3 дополнительных пикселей, о которых он не упоминает в статье.

Совместное использование параметров. Схема совместного использования параметров используется в сверточных слоях для управления количеством параметров. Используя приведенный выше пример из реальной жизни, мы видим, что в первом слое Conv 55 * 55 * 96 = 290 400 нейронов, и каждый из них имеет 11 * 11 * 3 = 363 веса и 1 смещение. В совокупности это дает 290400 * 364 = 105 705 600 параметров только на первом уровне ConvNet. Понятно, что это очень большое число.

Оказывается, что мы можем значительно сократить число параметров, если сделать одно разумное допущение: если один признак полезен для вычисления в некотором пространственном положении (x,y), то он также должен быть полезен для вычисления в другом положении ($x_2, y_2$). Другими словами, обозначив один двумерный срез глубины как срез глубины (например, объем размером [55x55x96] имеет 96 срезов глубины, каждый размером [55x55]), мы собираемся ограничить нейроны в каждом срезе глубины, чтобы они использовали одни и те же веса и смещение. При такой схеме распределения параметров первый слой Conv в нашем примере теперь будет иметь только 96 уникальных наборов весов (по одному для каждого среза глубины), что в сумме составит 96 * 11 * 11 * 3 = 34 848 уникальных весов, или 34 944 параметра (+96 смещений). В качестве альтернативы, все 55*55 нейронов в каждом срезе глубины теперь будут использовать одни и те же параметры. На практике во время обратного распространения каждый нейрон в объеме будет вычислять градиент для своих весов, но эти градиенты будут суммироваться для каждого среза глубины и обновлять только один набор весов для каждого среза.

Обратите внимание, что если все нейроны в одном срезе глубины используют один и тот же вектор весов, то прямой проход слоя CONV в каждом глубинном срезе может быть вычислен как свертка весов нейрона с входным объемом (отсюда и название: сверточный слой). Вот почему принято называть наборы весов фильтром (или ядром), который свертывается с входными данными.

Примеры фильтров, изученных Крижским и др. Каждый из 96 показанных здесь фильтров имеет размер [11x11x3], и каждый из них является общим для нейронов 55 * 55 в одном глубинном срезе. Обратите внимание, что предположение о совместном использовании параметров относительно разумно: если обнаружение горизонтального края важно в каком-то месте изображения, оно должно быть интуитивно полезным и в каком-то другом месте из-за трансляционно-инвариантной структуры изображений. Таким образом, нет необходимости заново учиться обнаруживать горизонтальный ребро в каждом из 55 * 55 различных мест в выходном объеме слоя Conv.

Обратите внимание, что иногда предположение о совместном использовании параметров может не иметь смысла. Это особенно верно в том случае, когда входные изображения в ConvNet имеют некоторую специфическую центрированную структуру, где мы должны ожидать, например, что на одной стороне изображения должны быть изучены совершенно разные функции, чем на другой. Одним из практических примеров является ситуация, когда входными данными являются лица, которые были центрированы на изображении. Можно ожидать, что различные особенности, специфичные для глаз или волос, могут (и должны) быть изучены в разных пространственных местах. В этом случае обычно ослабляют схему совместного использования параметров и вместо этого просто называют слой локально подключенным слоем.

Нумерные примеры. Чтобы сделать обсуждение выше более конкретным, давайте выразим те же идеи, но в коде и на конкретном примере. Предположим, что входной объем представляет собой массив numpy. Тогда:X - Колонка глубины (или волокно) в позиции будет активацией.(x,y) X[x,y,:] - Глубинным срезом или, что эквивалентноd, картой активации на глубине были бы активации X[:,:,d] .

Пример слоя conv. Предположим, что входной объем имеет форму . Предположим далее, что мы не используем нулевое заполнение (X X.shape: (11,11,4)P=0), что размер фильтра равен F=5, и что шаг является S=2. Таким образом, выходной объем будет иметь пространственный размер (11-5)/2+1 = 4, что дает объем с шириной и высотой 4. Карта активации в выходном объеме (назовем его ) будет выглядеть следующим образом (в этом примере вычисляются только некоторые элементы):V - V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0 - V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0 - V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0 - V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

Помните, что в numpy приведенная выше операция обозначает поэлементное умножение между массивами. Заметьте также, что вектор веса — это вектор веса этого нейрона и смещение. Здесь предполагается, что он имеет форму , так как размер фильтра равен 5, а глубина входного объема равна 4. Обратите внимание, что в каждой точке мы вычисляем скалярное произведение, как это было показано ранее в обычных нейронных сетях. Кроме того, мы видим, что мы используем тот же вес и смещение (из-за совместного использования параметров), и где размеры по ширине увеличиваются с шагом 2 (т.е. шаг). Чтобы построить вторую карту активации в выходном объеме, у нас есть:* W0 b0 W0 W0.shape: (5,5,4)
- V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1 - V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1 - V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1 - V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1 - V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (пример перехода по y) - V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (или по обоим)

где мы видим, что мы индексируем второе измерение глубины в V (по индексу 1), потому что мы вычисляем вторую карту активации, и что теперь используется другой набор параметров (W1). В приведенном выше примере мы для краткости опускаем некоторые другие операции, которые Conv Layer выполнил бы для заполнения других частей выходного массива V. Кроме того, вспомните, что эти карты активации часто отслеживаются по элементам с помощью функции активации, такой как ReLU, но здесь это не показано.

Резюме. Подводя итог, можно сказать, что слой Conv:

Принимает объем любого размера $W_1 \times H_1 \times D_1$
Требуется четыре гиперпараметра:
- Количество фильтров K,
- их пространственная протяженность F,
- Шаг вперед S,
- Величина нулевого отступа P.
Производит объем большого размера $W_2 \times H_2 \times D_2$ где:
- W2=(W1−F+2P)/S+1
- H2=(H1−F+2P)/S+1 (т.е. ширина и высота вычисляются поровну по симметрии)
- D2=K
Благодаря совместному использованию параметров он вводит $F \cdot F \cdot D_1$ веса на фильтр, итого $(F \cdot F \cdot D_1) \cdot K$ веса и K cмещений.
В выходном объеме метод d-я глубина среза (размера $W_2 \times H_2$ ) является результатом выполнения валидной свертки d-й фильтр по входной громкости с шагом S, а затем сместить на d-ое смещение.

Общая настройка гиперпараметров выглядит следующим образом: F=3,S=1,P=1. Тем не менее, существуют общие условности и эмпирические правила, которые мотивируют эти гиперпараметры. Смотрите раздел Архитектуры ConvNet ниже.

Демо свертки. Ниже приведена бегущая демонстрация слоя CONV. Поскольку 3D-объемы трудно визуализировать, все объемы (входной объем (синий), весовой объем (красный), выходной объем (зеленый)) визуализируются с каждым срезом глубины, уложенным в ряды. Входной объем имеет размер $W_1 = 5, H_1 = 5, D_1 = 3$, а параметры слоя CONV равны $K = 2, F = 3, S = 2, P = 1$. То есть у нас есть два фильтра размера 3×3, и наносятся они с шагом 2. Следовательно, размер выходного объема имеет пространственный размер (5 - 3 + 2)/2 + 1 = 3. Кроме того, обратите внимание, что отступ P=1 применяется к входному объему, при этом внешняя граница входного объема обнуляется. На приведенной ниже визуализации перебираются выходные активации (зеленый) и показано, что каждый элемент вычисляется путем поэлементного умножения выделенных входных данных (синий) на фильтр (красный), суммирования его и последующего смещения результата.

- !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! -

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Реализация в виде умножения матриц. Обратите внимание, что операция свертки по сути выполняет скалярное произведение между фильтрами и локальными областями входных данных. Общий шаблон реализации слоя CONV заключается в том, чтобы воспользоваться этим фактом и сформулировать прямой проход сверточного слоя в виде умножения одной большой матрицы следующим образом: _ Локальные регионы на входном изображении растягиваются в столбцы с помощью операции, обычно называемой im2col. Например, если входной параметр имеет размер [227x227x3] и он должен быть свернут с помощью фильтров 11x11x3 на шаге 4, то мы возьмем [11x11x3] блоков пикселей на входе и растянем каждый блок в вектор-столбец размером 11113 = 363. Повторение этого процесса на входе с шагом 4 дает (227-11)/4+1 = 55 позиций как по ширине, так и по высоте, что приводит к выходной матрице im2col размера [363 x 3025], где каждый столбец представляет собой растянутое восприимчивое поле, и всего их 55 x 55 = 3025. Обратите внимание, что поскольку рецептивные поля перекрываются, каждое число во входном объеме может дублироваться в нескольких отдельных столбцах.X_col - Грузы слоя CONV аналогичным образом растягиваются в ряды. Например, если имеется 96 фильтров размера [11x11x3], то получится матрица размера [96 x 363]. W_row - Результат свертки теперь эквивалентен выполнению одного умножения большой матрицы , которое вычисляет скалярное произведение между каждым фильтром и каждым местоположением восприимчивого поля. В нашем примере результатом этой операции будет [96 x 3025], что дает выходные данные скалярного произведения каждого фильтра в каждом месте.np.dot(W_row, X_col) - В конечном итоге результат должен быть возвращен к его надлежащему выходному размеру [55x55x96].

У этого подхода есть недостаток, заключающийся в том, что он может использовать много памяти, так как некоторые значения во входном объеме многократно реплицируются в . Тем не менее, преимущество заключается в том, что существует множество очень эффективных реализаций матричного умножения, которыми мы можем воспользоваться (например, в широко используемом BLAS API). Более того, та же идея im2col может быть повторно использована для выполнения операции объединения, о которой мы поговорим далее.X_col

Обратное распространение. Обратный проход для операции свертки (как для данных, так и для весов) также является сверткой (но с пространственно перевернутыми фильтрами). Это легко вывести в одномерном случае с помощью примера с игрушкой (пока не раскрывается).

Свертка 1х1. В качестве отступления, в нескольких работах используются свертки 1x1, впервые исследованные Network in Network. Некоторые люди поначалу путаются, видя свертки 1x1, особенно когда они исходят из фона обработки сигналов. Обычно сигналы двумерны, поэтому свертки 1x1 не имеют смысла (это просто поточечное масштабирование). Однако в ConvNet это не так, потому что необходимо помнить, что мы работаем с трехмерными объемами и что фильтры всегда распространяются на всю глубину входного объема. Например, если входные данные равны [32x32x3], то выполнение сверток 1x1 фактически будет выполнением трехмерных скалярных произведений (поскольку глубина входных данных равна 3 каналам).

Расширенные извилины. Недавняя разработка (см., например, статью Фишера Ю. и Владлена Колтуна) заключается в введении еще одного гиперпараметра в слой CONV, называемого дилатацией. До сих пор мы обсуждали только непрерывные фильтры CONV. Тем не менее, можно иметь фильтры, которые имеют промежутки между каждой клеткой, называемые расширением. Например, в одном измерении фильтр размера 3 будет вычислять на входных данных следующее: . Это расширение до 0. Для расширения 1 фильтр вместо этого будет вычислять ; Другими словами, между заявками есть разрыв в 1. Это может быть очень полезно в некоторых настройках для использования в сочетании с фильтрами 0-расширения, поскольку это позволяет объединять пространственную информацию по входным данным гораздо более агрессивно с меньшим количеством слоев. Например, если вы наложите два слоя CONV 3x3 друг на друга, то вы можете убедить себя, что нейроны на втором слое являются функцией участка входного сигнала 5x5 (мы бы сказали, что эффективное рецептивное поле этих нейронов равно 5x5). Если мы будем использовать расширенные извилины, то это эффективное рецептивное поле будет расти гораздо быстрее.w x w[0]*x[0] + w[1]*x[1] + w[2]*x[2]w[0]*x[0] + w[1]*x[2] + w[2]*x[4]

Слой пула

В архитектуре ConvNet обычно периодически вставляется слой Pooling между последовательными слоями Conv. Его функция состоит в том, чтобы постепенно уменьшать пространственный размер представления для уменьшения количества параметров и вычислений в сети и, следовательно, также контролировать переобучение. Слой пулинга работает независимо на каждом срезе глубины входных данных и изменяет его пространственный размер с помощью операции MAX. Наиболее распространенной формой является пулинговый слой с фильтрами размером 2x2, применяемыми с шагом 2 вниздискретизации каждого глубинного среза на входе на 2 по ширине и высоте, отбрасывая 75% активаций. Каждая операция MAX в этом случае будет принимать максимум более 4 чисел (маленькая область 2x2 в некотором глубинном срезе). Размер глубины остается неизменным. В более общем смысле, пуловый слой: - Принимает объем любого размера W1×H1×D1 - Требуется два гиперпараметра: - их пространственная протяженность F, - Шаг вперед S, - Производит объем большого размера $W_2 \times H_2 \times D_2$ где: - $W_2 = (W_1 - F)/S + 1$ - $H_2 = (H_1 - F)/S + 1$ - $D_2 = D_1$ - Вводит нулевые параметры, так как вычисляет фиксированную функцию входных данных - Для слоев Pooling заполнение входных данных не является обычным способом с использованием нулевого отступа.

Стоит отметить, что на практике встречаются только два распространенных варианта максимального слоя пула: Слой пулинга с F=3,S=2 (также называемое перекрывающимся пулом) и чаще F=2,S=2. Объединение размеров с большими рецептивными полями слишком разрушительно.

Общий пул. В дополнение к максимальному объединению, единицы объединения могут выполнять и другие функции, такие как усредненное объединение или даже объединение по L2-норме. Исторически часто использовалось среднее объединение, но в последнее время оно вышло из моды по сравнению с операцией максимального объединения, которая, как было показано, работает лучше на практике.

Пулинг слоя понижает дискретизацию объема пространственно, независимо в каждом глубинном срезе входного объема. Сверху: В этом примере входной объем размера [224x224x64] объединяется с фильтром размера 2, шаг 2 в выходной объем размера [112x112x64]. Обратите внимание, что глубина объема сохраняется. Снизу: Наиболее распространенной операцией понижения дискретизации является max, что приводит к максимальному объединению, показанному здесь с шагом 2. То есть, каждый макс берется над 4 числами (маленький квадратик 2х2).

Обратное распространение. Вспомните из главы об обратном распространении, что обратный проход для операции max(x, y) имеет простую интерпретацию как только маршрутизацию градиента на вход, который имел наибольшее значение в прямом проходе. Следовательно, во время прямого прохождения пулового слоя обычно отслеживают индекс максимальной активации (иногда также называемый переключателями), чтобы градиентная маршрутизация была эффективной во время обратного распространения.

Избавление от пулов. Многим людям не нравится операция по объединению, и они думают, что мы можем обойтись без нее. Например, Pursuit for Simplicity: The All Convolutional Net предлагает отказаться от пулового слоя в пользу архитектуры, состоящей только из повторяющихся слоев CONV. Чтобы уменьшить размер представления, они предлагают время от времени использовать больший шаг в слое CONV. Также было обнаружено, что отказ от слоев пула важен для обучения хороших генеративных моделей, таких как вариационные автоэнкодеры (VAE) или генеративно-состязательные сети (GAN). Вполне вероятно, что в будущих архитектурах будет очень мало или вообще не будет слоев пула.

Слой нормализации

Многие типы уровней нормализации были предложены для использования в архитектурах ConvNet, иногда с намерением реализовать схемы торможения, наблюдаемые в биологическом мозге. Однако с тех пор эти слои вышли из моды, потому что на практике их вклад был минимальным, если вообще был. О различных типах нормализации см. обсуждение в API библиотеки cuda-convnet Алекса Крижевского.

Полносвязный слой

Нейроны в полностью связном слое имеют полные связи со всеми активациями в предыдущем слое, как это видно в обычных нейронных сетях. Таким образом, их активации могут быть вычислены с помощью умножения матриц с последующим смещением смещения. Дополнительные сведения см. в разделе «Нейронные сети» примечаний.

Преобразование слоев FC в слои CONV

Стоит отметить, что единственное различие между слоями FC и CONV заключается в том, что нейроны в слое CONV связаны только с локальной областью на входе, и что многие нейроны в объеме CONV имеют общие параметры. Тем не менее, нейроны в обоих слоях по-прежнему вычисляют точечные произведения, поэтому их функциональная форма идентична. Таким образом, оказывается, что можно преобразовывать между слоями FC и CONV: - Для любого слоя CONV существует слой FC, реализующий ту же прямую функцию. Матрица весов будет большой матрицей, которая в основном равна нулю, за исключением некоторых блоков (из-за локальной связности), где веса во многих блоках равны (из-за совместного использования параметров). - И наоборот, любой слой FC может быть преобразован в слой CONV. Например, слой FC с K=4096, то есть с учетом некоторого входного объема размера 7×7×512 может быть эквивалентно выражен в виде слоя CONV с помощью F=7,P=0,S=1,K=4096. Другими словами, мы устанавливаем размер фильтра точно равным размеру входного объема, и, следовательно, на выходе будет просто 1×1×4096 так как только один столбец глубины «помещается» поперек входного объема, давая тот же результат, что и исходный слой FC.

Конверсия FC->CONV. Из этих двух преобразований возможность преобразования слоя FC в слой CONV особенно полезна на практике. Рассмотрим архитектуру ConvNet, которая берет изображение размером 224x224x3, а затем использует ряд слоев CONV и слоев POOL для уменьшения объема активации до размера 7x7x512 (в архитектуре AlexNet, которую мы увидим позже, это делается с помощью 5 слоев пула, которые каждый раз уменьшают пространственную дискретизацию входных данных в два раза). Получаем итоговый пространственный размер 224/2/2/2/2/2 = 7). После этого AlexNet использует два слоя FC размера 4096 и, наконец, последний слой FC с 1000 нейронами, которые вычисляют баллы класса. Мы можем преобразовать каждый из этих трех слоев FC в слои CONV, как описано выше: - Замените первый слой FC, который смотрит на объем [7x7x512], на слой CONV, использующий размер фильтра F=7, дающий выходной объем [1x1x4096]. - Замените второй слой FC на слой CONV, использующий размер фильтра F=1, дающий выходной объем [1x1x4096] - Замените последний слой FC аналогичным образом, на F=1, выдающий итоговый вывод [1x1x1000]

Каждое из этих преобразований на практике может включать в себя манипуляции (например, изменение формы) матрицей весов W в каждом слое FC в фильтры слоя CONV. Оказывается, что это преобразование позволяет нам очень эффективно «скользить» по исходной ConvNet через множество пространственных положений в более крупном изображении за один проход вперед.

Например, если образ 224x224 дает объем размера [7x7x512] - т.е. уменьшение на 32, то пересылка образа размера 384x384 через преобразованную архитектуру даст эквивалентный объем в размере [12x12x512], так как 384/32 = 12. Последующие 3 слоя CONV, которые мы только что преобразовали из слоев FC, теперь дадут окончательный объем размера [6x6x1000], поскольку (12 - 7)/1 + 1 = 6. Обратите внимание, что вместо одного вектора оценок классов размера [1x1x1000] мы теперь получаем целый массив оценок классов 6x6 на изображении 384x384.

Независимая оценка исходной ConvNet (со слоями FC) по кадрам 224x224 изображения 384x384 с шагом 32 пикселя дает результат, идентичный однократной пересылке преобразованной ConvNet.

Естественно, пересылка преобразованной ConvNet за один раз гораздо эффективнее, чем итерация исходной ConvNet по всем этим 36 местоположениям, поскольку 36 оценок используют общие вычисления. Этот трюк часто используется на практике для повышения производительности, когда, например, обычно изменяют размер изображения, чтобы сделать его больше, используют преобразованный ConvNet для оценки оценок класса во многих пространственных положениях, а затем усредняют баллы класса.

Наконец, что, если мы хотим эффективно применить исходную ConvNet поверх изображения, но с шагом меньше 32 пикселей? Мы могли бы добиться этого с помощью нескольких передач вперед. Например, обратите внимание, что если бы мы хотели использовать шаг в 16 пикселей, мы могли бы сделать это, объединив объемы, полученные при пересылке преобразованной ConvNet дважды: сначала над исходным изображением, а затем над изображением, но с пространственным сдвигом изображения на 16 пикселей как по ширине, так и по высоте.

Блокнот IPython по сетевой хирургии показывает, как выполнить преобразование на практике, в коде (с использованием Caffe)

Архитектуры ConvNet

Мы видели, что сверточные сети обычно состоят только из трех типов слоев: CONV, POOL (мы предполагаем Max pool, если не указано иное) и FC (сокращение от fully connected). Мы также явно напишем функцию активации RELU в виде слоя, который применяет элементную нелинейность. В этом разделе мы обсудим, как они обычно складываются в целые ConvNet.

Узоры слоев

Наиболее распространенная форма архитектуры ConvNet состоит из нескольких слоев CONV-RELU, затем за ними следуют слои POOL и повторяет этот шаблон до тех пор, пока изображение не будет объединено в пространстве до небольшого размера. В какой-то момент часто происходит переход к полносвязным слоям. Последний полносвязный слой содержит выходные данные, такие как баллы класса. Другими словами, наиболее распространенная архитектура ConvNet следует шаблону:

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

где * указывает на повторение, а POOL? указывает на необязательный слой пула. Более того, N >= 0 (и обычно N <= 3 M >= 0 K >= 0), , (и обычно K < 3 ). Например, вот некоторые распространенные архитектуры ConvNet, которые следуют этому шаблону:
- INPUT -> FC реализует линейный классификатор. Здесь N = M = K = 0 - INPUT -> CONV -> RELU -> FC - INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. Здесь мы видим, что между каждым слоем POOL есть один слой CONV. -INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC. Здесь мы видим два слоя CONV, расположенных перед каждым слоем POOL. Как правило, это хорошая идея для более крупных и глубоких сетей, поскольку несколько слоев CONV могут привести к более сложным характеристикам входного объема перед деструктивной операцией объединения.

Отдайте предпочтение стеку небольших фильтров CONV одному большому слою рецептивного поля CONV. Предположим, что вы накладываете три слоя CONV 3x3 друг на друга (конечно, с нелинейностями между ними). При таком расположении каждый нейрон на первом слое CONV имеет представление входного объема 3x3. Нейрон на втором слое CONV имеет представление 3x3 первого слоя CONV и, следовательно, представление входного объема 5x5. Аналогично, нейрон на третьем слое CONV имеет представление 3x3 на 2-й слой CONV и, следовательно, на входной объем 7x7. Предположим, что вместо этих трех слоев 3x3 CONV мы хотим использовать только один слой CONV с рецептивными полями 7x7. Эти нейроны будут иметь размер рецептивного поля входного объема, идентичный в пространственном масштабе (7x7), но с некоторыми недостатками. - Во-первых, нейроны будут вычислять линейную функцию над входными данными, в то время как три стека слоев CONV содержат нелинейности, которые делают их особенности более выразительными. - Во-вторых, если мы предположим, что все тома имеют C каналов, то можно видеть, что один слой 7x7 CONV будет содержать $C \times (7 \times 7 \times C) = 49 C^2$ параметры, в то время как три слоя 3x3 CONV будут содержать только $3 \times (C \times (3 \times 3 \times C)) = 27 C^2$ параметры. Интуитивно понятно, что наложение слоев CONV с маленькими фильтрами в отличие от одного слоя CONV с большими фильтрами позволяет нам выразить более мощные функции входных данных с меньшим количеством параметров. В качестве практического недостатка нам может потребоваться больше памяти для хранения всех результатов промежуточного слоя CONV, если мы планируем использовать обратное распространение.

Недавние уходы. Следует отметить, что традиционная парадигма линейного списка слоев в последнее время была поставлена под сомнение в архитектурах Google Inception, а также в современных (современных) Residual Networks от Microsoft Research Asia. Оба они (см. подробности ниже в разделе тематических исследований) имеют более сложные и разные структуры подключения.

__На практике: используйте то, что лучше всего работает на ImageNet__. Если вы чувствуете некоторую усталость, думая об архитектурных решениях, вам будет приятно узнать, что в 90% или более приложений вам не нужно беспокоиться об этом. Я предпочитаю резюмировать этот момент как «не будьте героем» : вместо того, чтобы создавать свою собственную архитектуру для решения проблемы, вы должны посмотреть, какая архитектура в настоящее время лучше всего работает на ImageNet, загрузить предварительно обученную модель и настроить ее на основе ваших данных. В редких случаях приходится обучать ConvNet с нуля или проектировать его с нуля. Я также говорил об этом в школе Deep Learning.

Шаблоны для определения размеров слоев

До сих пор мы опускали упоминания об общих гиперпараметрах, используемых на каждом из уровней ConvNet. Сначала мы изложим общие эмпирические правила для определения размеров архитектур, а затем будем следовать правилам, обсуждая нотацию:

Входной слой (содержащий изображение) должен быть кратен 2 много раз. К распространенным номерам относятся 32 (например, CIFAR-10), 64, 96 (например, STL-10) или 224 (например, общие ImageNet ConvNet), 384 и 512.

Для конвальных слоев следует использовать небольшие фильтры (например, 3x3 или максимум 5x5), с шагом S=1 и, что особенно важно, заполнение входного объема нулями таким образом, чтобы слой conv не изменял пространственные размеры входных данных. То есть, когда F=3, то с помощью P=1 сохранит исходный размер входных данных. Когда F=5, P=2. Для генерала F, видно, что P=(F−1)/2 cохраняет размер ввода. Если вам нужно использовать фильтры большего размера (например, 7x7 или около того), это обычно можно увидеть только на самом первом выпуклом слое, который смотрит на входное изображение.

Слои пула отвечают за понижение дискретизации пространственных размеров входных данных. Наиболее распространенной настройкой является использование max-pooling с рецептивными полями 2x2 (т.е. F=2), и с шагом 2 (т.е. S=2). Обратите внимание, что при этом отбрасывается ровно 75% активаций входного объема (из-за уменьшения дискретизации на 2 раза как по ширине, так и по высоте). Другой, чуть менее распространенный вариант — использование рецептивных полей 3x3 с шагом 2, но это делает «подгонку» более сложной (например, слой 32x32x3 потребует нулевого заполнения для использования с максимальным объединением полей с рецептивным полем 3x3 и шагом 2). Очень редко можно увидеть, что размеры рецептивных полей для максимального пула больше 3, потому что в этом случае пулинг слишком потерян и агрессивен. Обычно это приводит к ухудшению производительности.

Уменьшение головной боли при уменьшении размера. Представленная выше схема радует тем, что все слои CONV сохраняют пространственный размер входных данных, в то время как только слои POOL отвечают за пространственное понижение объемов. В альтернативной схеме, где мы используем шаги больше 1 или не обнуляем входные данные в слоях CONV, нам пришлось бы очень тщательно отслеживать входные объемы по всей архитектуре CNN и убедиться, что все шаги и фильтры «работают» , и что архитектура ConvNet хорошо и симметрично связана.

Зачем использовать strace of 1 в CONV? Меньшие шаги лучше работают на практике. Кроме того, как уже упоминалось, шаг 1 позволяет нам оставить всю пространственную понижение дискретизации слоям POOL, при этом слои CONV преобразуют только входной объем по глубине.

Зачем использовать набивку? В дополнение к вышеупомянутому преимуществу сохранения постоянных пространственных размеров после CONV, это фактически повышает производительность. Если бы слои CONV не обнуляли входные данные, а выполняли только корректные свертки, то размер объемов уменьшался бы на небольшую величину после каждого CONV, а информация на границах «смывалась» бы слишком быстро.

Компрометация из-за ограничений памяти. В некоторых случаях (особенно на ранних этапах архитектуры ConvNet) объем памяти может очень быстро увеличиваться с помощью эмпирических правил, представленных выше. Например, фильтрация изображения размером 224x224x3 с тремя слоями CONV 3x3 с 64 фильтрами каждый и отступом 1 создаст три объема активации размером [224x224x64]. Это составляет в общей сложности около 10 миллионов активаций, или 72 МБ памяти (на изображение, как для активаций, так и для градиентов). Поскольку графические процессоры часто имеют узкие места из-за памяти, может потребоваться пойти на компромисс. На практике люди предпочитают идти на компромисс только на первом уровне CONV сети. Например, одним из компромиссов может быть использование первого слоя CONV с размерами фильтра 7x7 и шагом 2 (как в сети ZF). В качестве другого примера, AlexNet использует размеры фильтров 11x11 и stride 4.

Тематические исследования

В области сверточных сетей существует несколько архитектур, которые имеют название. Наиболее распространенными являются:

LeNet. Первые успешные приложения сверточных сетей были разработаны Яном Лекуном в 1990-х годах. Из них наиболее известной является архитектура LeNet, которая использовалась для чтения почтовых индексов, цифр и т. д.
AlexNet. Первой работой, которая популяризировала сверточные сети в компьютерном зрении, стала сеть AlexNet, разработанная Алексом Крижевским, Ильей Суцкевером и Джеффом Хинтоном. В 2012 году AlexNet был представлен на конкурс ImageNet ILSVRC и значительно превзошел занявшего второе место (ошибка в топ-5 16% по сравнению с ошибкой в 26%, занявшей второе место). Сеть имела очень похожую архитектуру на LeNet, но была глубже, больше и включала сверточные слои, наложенные друг на друга (ранее было обычным делом иметь только один слой CONV, за которым всегда следовал слой POOL).
ZF Net. Победителем ILSVRC 2013 стала сверточная сеть от Мэтью Зейлера и Роба Фергуса. Она стала известна как ZFNet (сокращение от Zeiler & Fergus Net). Это было усовершенствование AlexNet за счет настройки гиперпараметров архитектуры, в частности, за счет увеличения размера средних сверточных слоев и уменьшения размера шага и фильтра на первом слое.
GoogLeNet. Победителем ILSVRC 2014 стала сверточная сеть от Сегеди и др. от Google. Ее основным вкладом стала разработка модуля Inception, который значительно сократил количество параметров в сети (4M, по сравнению с AlexNet с 60M). Кроме того, в этой статье используется Average Pooling вместо Fully Connected layers в верхней части ConvNet, что устраняет большое количество параметров, которые не имеют большого значения. Существует также несколько последующих версий GoogLeNet, последняя из которых Inception-v4.
VGGNet. Второе место на ILSVRC 2014 заняла сеть Карена Симоняна и Эндрю Зиссермана, которая стала известна как VGGNet. Его основной вклад заключался в том, что он показал, что глубина сети является критически важным компонентом для хорошей производительности. Их окончательная лучшая сеть содержит 16 слоев CONV/FC и, что привлекательно, отличается чрезвычайно однородной архитектурой, которая выполняет только свертки 3x3 и пул 2x2 от начала до конца. Их предварительно обученная модель доступна для использования в Caffe по принципу «подключи и работай». Недостатком VGGNet является то, что он дороже в оценке и использует гораздо больше памяти и параметров (140M). Большинство этих параметров находятся в первом полностью связанном слое, и с тех пор было обнаружено, что эти слои FC могут быть удалены без снижения производительности, что значительно сокращает количество необходимых параметров.
ResNet.. Остаточная сеть, разработанная Каим Хе и др., стала победителем ILSVRC 2015. Она оснащена специальными соединениями для пропуска и интенсивным использованием пакетной нормализации. В архитектуре также отсутствуют полностью связанные слои в конце сети. Читателю также предлагается ознакомиться с презентацией Кайминга (видео, слайды) и некоторыми недавними экспериментами, которые воспроизводят эти сети в Torch. В настоящее время ResNet являются самыми современными моделями сверточных нейронных сетей и являются выбором по умолчанию для использования ConvNet на практике (по состоянию на 10 мая 2016 года). В частности, см. более поздние разработки, которые корректируют исходную архитектуру, из книги Каим Хе и др. IСопоставления идентификационных данных в глубоких остаточных сетях (опубликована в марте 2016 г.).

VGGNet в деталях. Давайте разберем VGGNet более подробно в качестве тематического исследования. Вся сеть VGGNet состоит из слоев CONV, которые выполняют свертки 3x3 со stride 1 и pad 1, и из слоев POOL, которые выполняют 2x2 max pooling с stride 2 (и без отступа). Мы можем записывать размер представления на каждом шаге обработки и отслеживать как размер представления, так и общее количество весов:

INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000

TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

Как и в случае со сверточными сетями, обратите внимание, что большая часть памяти (а также вычислительного времени) используется в ранних слоях CONV, а большинство параметров — в последних слоях FC. В данном конкретном случае первый слой FC содержит 100 м грузов из общего числа 140 м.

Вычислительные соображения

Самым большим узким местом, о котором следует знать при создании архитектур ConvNet, является узкое место памяти. Многие современные графические процессоры имеют ограничение в 3/4/6 ГБ памяти, а лучшие графические процессоры имеют около 12 ГБ памяти. Существует три основных источника памяти, которые необходимо отслеживать:

Из промежуточных размеров объемов: Это исходное количество активаций на каждом уровне ConvNet, а также их градиенты (одинакового размера). Как правило, большая часть активаций происходит на более ранних уровнях ConvNet (т.е. на первых уровнях Conv). Они сохраняются, потому что они нужны для обратного распространения, но умная реализация, которая запускает ConvNet только во время тестирования, в принципе могла бы значительно сократить это, сохраняя только текущие активации на любом уровне и отбрасывая предыдущие активации на уровнях ниже.
Из размеров параметров: Это числа, которые содержат параметры сети, их градиенты во время обратного распространения и, как правило, также кэш шагов, если оптимизация выполняется с использованием momentum, Adagrad или RMSProp. Следовательно, память для хранения только вектора параметров обычно должна быть умножена по крайней мере на 3 или около того.
Каждая реализация ConvNet должна поддерживать различную память, такую как пакеты данных изображений, возможно, их дополненные версии и т.д.

После того, как вы получили приблизительную оценку общего количества значений (для активаций, градиентов и разного), это число следует преобразовать в размер в ГБ. Возьмите количество значений, умножьте на 4, чтобы получить исходное количество байтов (поскольку каждая плавающая точка равна 4 байтам, или, возможно, на 8 для двойной точности), а затем разделите на 1024 несколько раз, чтобы получить объем памяти в КБ, МБ и, наконец, в ГБ. Если ваша сеть не подходит, обычной эвристикой для «подгонки» является уменьшение размера пакета, поскольку большая часть памяти обычно потребляется активациями.

Дополнительные материалы

Дополнительные ресурсы, связанные с реализацией:

Бенчмарки Soumith для производительности CONV
Демонстрация ConvNetJS CIFAR-10 позволяет экспериментировать с архитектурами ConvNet и видеть результаты и вычисления в режиме реального времени, в браузере.
Caffe, одна из популярных библиотек ConvNet.
Современные ResNet в Torch7

Классификация изображений

Введение в классификацию изображений

Классификатор ближайшего соседа

Классификатор k - ближайших соседей

Наборы данных и настройки гиперпараметров

Применение kNN на практике

Дополнительные материалы

Понимание и визуализация

Визуализация активаций и веса первого слоя

Получение изображений, которые максимально активируют нейрон

Встраивание кодов с помощью t-SNE

Окклюзия частей изображения

Визуализация градиента данных и его друзей

Восстановление оригинальных изображений на основе кодов CNN

Какой объем пространственной информации сохраняется?

Производительность построения графиков в зависимости от атрибутов изображения

Обман ConvNet

Сравнение ConvNet с людьми-маркировщиками

Архитектура нейросетей

Сверточные нейронные сети (CNNs / ConvNets)

Обзор архитектуры

Слои, используемые для построения ConvNet

Сверточный слой

Слой пула

Слой нормализации

Полносвязный слой

Преобразование слоев FC в слои CONV

Архитектуры ConvNet

Узоры слоев

Шаблоны для определения размеров слоев

Тематические исследования

Вычислительные соображения

Дополнительные материалы